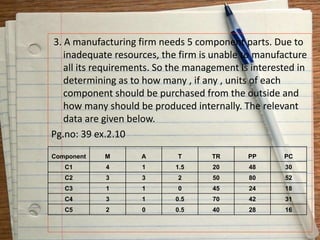
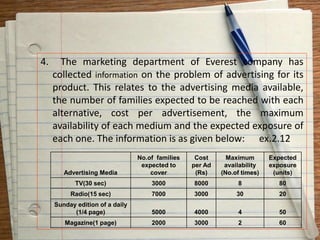
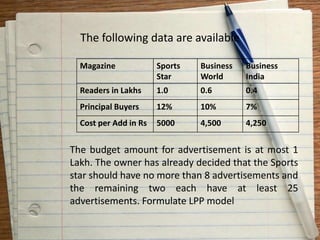
This document provides an introduction to operations research. It defines operations research as a scientific approach to decision making that seeks to determine how best to operate a system under conditions of allocating scarce resources. The document discusses the origin and applications of operations research. It also outlines some common operations research techniques like linear programming, transportation problems, assignment problems, and PERT-CPM. Finally, it provides definitions of operations research from different authors and discusses the scope and methodology of operations research.

1. Operations research-Introduction
MRS.KIRANMAYI PATEL

2. What is Operations Research?

3. Operations research
• Operations research is a “scientific approach to
decision making , which seeks to determine how best
to design and operate a system, under conditions
requiring the allocation of scarce resources”.
• Provides a set of algorithms that act as tools for
effective problem solving and decision making
• Extensive applications in engineering, business and
public systems.
• Used extensively by manufacturing and service
industries in decision making.

4. Operations research
• Origin during World War II when the British military
asked scientists to analyze military problems.
• The application of mathematics and scientific method to
military applications was called Operations Research.
• Today it is also called Management science.
• It is a scientific approach to decision making that seeks to
determine how best to operate a system under
conditions of allocating scarce resources.

5. Operations research
• Linear Programming-Formulations
• Linear Programming-Solutions
• Transport Problem
• Assignment Problem
• Game Theory
• Decision Theory
• PERT - CPM

6. Decision Making and Quantitative
Techniques
Decision making involves choosing a
course of action from various
available alternatives

7. Meaning Of OR:
According to T.L.Saaty “OR is the art of giving bad results
to problems to which otherwise worse results are
given”.
According to Churchman “OR is the application of
scientific methods, techniques and tools to problems
involving the operations of systems so as to provide
these in control of the application with optimum
solutions to the problem”.
According to H.M.Wagner “ OR is the scientific approach
to problem solving for executive management”.

8. Scope of OR
• In Agriculture
• In Finance
• In Industry
• In Marketing
• In Production Management
• In Personnel Management

9. Characteristics Features of OR
• It is a scientific method employed for problem solving
and decision making by the management
The significant features are
1. Decision making
2. Scientific approach
3. objective
4. Inter-disciplinary team approach

10. Scientific Methodology?
• Defining a problem in a clear manner
• Collecting pertinent facts
• Analyzing the facts thoroughly
• Deriving and implementing solutions

11. Methodology Of OR:
Define the
Problem
Develop the
Model
Obtain Input
Data
Solve the Model
Model Validation
Analyze the results
Implement the Solution

12. What is Linear Programming Problem?
(LPP)

13. Linear Programming
• Linear Programming (LP)
– A family of mathematical techniques
(algorithms) that can be used for constrained
optimization problems with linear relationships.
• Graphical method
• Simplex method
– The problems must involve a single objective, a
linear objective function, and linear constraints
and have known and constant numerical values.

14. Decisions and Linear Programming
• Constrained optimization
– Finding the optimal solution to a problem
given that certain constraints must be satisfied
by the solution.
– A form of decision making that involves
situations in which the set of acceptable
solutions is somehow restricted.
– Recognizes scarcity—the limitations on the
availability of physical and human resources.
– Seeks solutions that are both efficient and
feasible in the allocation of resources.

15. Characteristics of LP Models

16. Formulating LP Models
• Formulating linear programming models
involves the following steps:
1. Define the decision variables.
2. Determine the objective function.
3. Identify the constraints.
4. Determine appropriate values for parameters and
determine whether an upper limit, lower limit, or
equality is called for.
5. Use this information to build a model.
6. Validate the model.

17. Formulation of LPP:
Step 1:Determine the objective function as a linear function of
the variables.
Step 2: Formulate the other conditions of the problem such as
resources limitations as linear equations or in equations in
terms of the variables.
Step 3: Add the non-negativity constraints.

18. • Small manufacturer making two products A and B.
• Two resources R1 and R2 are required to make these
products.
• each unit of product A requires 1 unit of R1 and 3 units of R2.
• each unit of product B requires 1 unit of R1 and 2 units of
R2.
• The Manufacturer has 5 units of R1 and 12 units of R2
available.
• The manufacturer also makes a profit of
-Rs 6 per unit of A sold and
-Rs5 per unit of B of sold.
Formulation – Product mix problem

19. Solution
• The manufacturer has to decide or determine how many
units of A, and how many units of B, he or she is going is to
produce.
• It is acceptable that the manufacturer would like to make as
much profit as possible and would decide on the
production quantities accordingly.
• The manufacturer has to ensure that the resources needed
to make the products are available.
• Before we attempt to find out the decisions of the
manufacturer let us redefine the problem in an algebraic
form.
• The manufacturer has to decide on the production
quantities. Let us call them X and Y and define.
• let X be the number of units of product A made
• Let Y be number of units of product B made.
• Cont…

20. 
The profit associated with X units of product A
and Y units of product B is 6X+5Y.
The manufacturer would determine X and Y such
that this function has a maximum value.
The requirements of the two resources are X+y
for R1 and 3X+2Y for R2 and the manufacturer has to ensure
that these are available.
The problem is to find X and Y such that 6X+5Y is
maximized and
Cont…

21. • X+Y≤5 and 3X+2Y ≤ 12 are satisfied. Also it is necessary
that X,Y≥0 so that only non negative quantities are
produced.
If we redefine the production quantities as X₁ and X₂ (for
uniformity and consistency) then
Maximize Z= 6X₁+5X₂
subject to X₁+X₂ ≤ 5
3X₁+2X₂ ≤ 12
X₁, X₂ ≥ 0

22. Terminology
• The problem variables X1 and X2 are called Decision
variables and they represent the solution or the output
decision from the problem.
• The profit function that the manufacturer wishes to
increase, represents the objective of making the
decisions on the production quantities and is called the
Objective Function

23. Terminology cont…
• The conditions matching the resources availability and
resources requirement are called Constraints.
- These usually limit (or restrict )the values the
decision variables can take.
• We have also explicitly stated that the decision variable
should take non negative values.
- This is true for all liner programming problems.
- This is called non negativity restriction.
• The problem that we have written down in algebraic
form represents the mathematical model of the given
system and is called the Problem Formulation.

24. A shop can make two types of sweets (A and B). They use two
resources – flour and sugar. To make one packet of A, they
need 3 kg of flour and 3 kg of sugar. To make one packet of B,
they need 3 kg of flour and 4 kg of sugar. They have 21 kg of
flour and 28 kg of sugar. These sweets are sold at Rs 1000 and
900 per packet respectively. Find the best product mix to
maximize the revenue.
Formulation – Product mix problem
Let X1 be the number of packets of sweet A made
Let X2 be the number of packets of sweet B made
Maximize 1000X1 + 900X2
3X1 + 3X2 ≤ 21
3X1 + 4X2 ≤ 28
X1, X2 ≥ 0

25. Notations
Let X1 be the number of packets of sweet A made
Let X2 be the number of packets of sweet B made
Maximize 1000X1 + 900X2
Decision
variable
Objective function
Constraints
3X1 + 3X2 ≤ 21
3X1 + 4X2 ≤ 28
X1, X2 ≥ 0
Non negativity restriction
Assumptions
1. Proportionality
2. Linearity
3. Deterministic

26. A company wants to advertise their product in four different
media – TV, newspaper, websites and radio. The reach per
advertisement in these four media are 8000, 5000, 3000 and
2000. The cost per advertisement is Rs 4 lakhs, 3 lakhs, 2 lakhs
and 1.5 lakhs. The maximum number of advertisements that
the company wishes to have in each media is 3, 4, 5, 4. The
budget available is 32 lakhs. How many advertisements does
the company decide in each media to maximize reach?
Let X1 be the number of advertisements in TV
Let X2 be the number of advertisements in newspaper
Let X3 be the number of advertisements in websites
Let X4 be the number of advertisements in radio
Formulation – Media selection problem

27. Formulation – Media Selection Problem
Maximize 8000X1 + 5000X2 + 3000X3 + 2000X4
subject to
4X1 + 3X2 + 2X3 + 1.5X4 ≤ 32
X1 ≤ 3
X2 ≤ 4
X3 ≤ 5
X4 ≤ 4
X1, X2, X3, X4 ≥ 0
Reach
Budget
Limits/bounds
Non negativity

28. A person requires 10,12, and 12 units chemicals A,B,C
for his garden. A liquid product contains 5,2 and 1
units of A,B and C respectively per jar. A dry product
contains 1,2 and 4 units of A,B,C per carton. If the
liquid product sells for Rs.3 per jar and the dry
product sells for Rs.2 per carton, how many of each
should be purchased in order to minimize the cost
and meet the requirements?
Formulation – Minimization problem

29. 1. A manufacturer produces two types of models A & B.
Each model A requires 4 hours of grinding and 2
hours of polishing, whereas model B requires 2 hours
of grinding and 5 hours of polishing. The
manufacturer has 2 grinders and 3 polishers. Each
grinder works for 40 hours a week and each polisher
works for 60 hours a week. Profit on model A is Rs.3
and on model B is Rs.4. Whatever is produced in a
week is sold in the market. How should the
manufacturer allocate his production capacity to the
types of models so that he may make the maximum
profit in week?
Practice Problems LP Formulations

30. 2. A toy company manufactures two types of dolls,
A and B. Each doll of type B takes twice as long to
produce as one of type A, and the company would
have time to make a maximum of 2000 per day. The
supply of plastic is sufficient to produce 1500 dolls
per day of A and B combined. Each B type doll
requires fancy dress of which there are only 600 per
day available. If the company makes a profit of Rs 3
and Rs. 5 on doll A and B respectively, then how
many dolls of A and B should be produced per day
in order to maximize the total profit. Formulate this
problem.

31. 3. A manufacturing firm needs 5 component parts. Due to
inadequate resources, the firm is unable to manufacture
all its requirements. So the management is interested in
determining as to how many , if any , units of each
component should be purchased from the outside and
how many should be produced internally. The relevant
data are given below.
Pg.no: 39 ex.2.10
Component M A T TR PP PC
C1 4 1 1.5 20 48 30
C2 3 3 2 50 80 52
C3 1 1 0 45 24 18
C4 3 1 0.5 70 42 31
C5 2 0 0.5 40 28 16

32. Where
M: Per unit milling time in hours
A: Per unit assembly time in hours
T: Per unit testing time in hours
TR: Total requirements in units
PP: Price per unit quoted in the market
PC: Per unit direct costs
Resources available are as follows:
Milling hours: 300
Assembly hours: 160
Testing hours: 150
Formulate this as an LPP, taking the objective function as
maximization of saving by producing the components
internally.

33. 4. The marketing department of Everest company has
collected information on the problem of advertising for its
product. This relates to the advertising media available,
the number of families expected to be reached with each
alternative, cost per advertisement, the maximum
availability of each medium and the expected exposure of
each one. The information is as given below: ex.2.12
Advertising Media
No.of families
expected to
cover
Cost
per Ad
(Rs)
Maximum
availability
(No.of times)
Expected
exposure
(units)
TV(30 sec) 3000 8000 8 80
Radio(15 sec) 7000 3000 30 20
Sunday edition of a daily
(1/4 page) 5000 4000 4 50
Magazine(1 page) 2000 3000 2 60

34. Other information and requirements:
a) The advertising budget is Rs 70,000
b) At least 40,000 families should be covered.
c) At least 2 insertions be given in Sunday edition of
a daily.
Formulate this as LPP to maximize the expected
exposure.

35. 5 .Advertising Media Selection Problem
The owner of a sports company wishes to determine
how many advertisements to place in the selected
three magazines Sports Star, Business World, Business
India. His objective is to advertise in such a way that
total exposure to principal buyers of sports goods is
maximized. The number of readers for each magazine
is known. Exposure in a particular magazine is the
number of advertisements placed multiplied by the
number of principal buyers.

36. The following data are available
Magazine Sports
Star
Business
World
Business
India
Readers in Lakhs 1.0 0.6 0.4
Principal Buyers 12% 10% 7%
Cost per Add in Rs 5000 4,500 4,250
The budget amount for advertisement is at most 1
Lakh. The owner has already decided that the Sports
star should have no more than 8 advertisements and
the remaining two each have at least 25
advertisements. Formulate LPP model