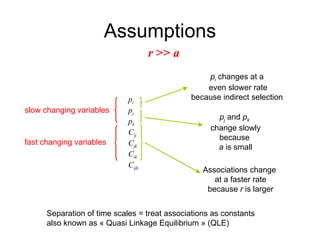
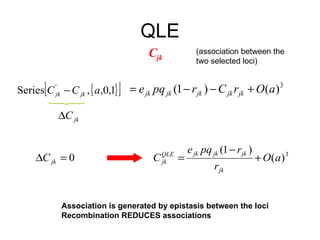
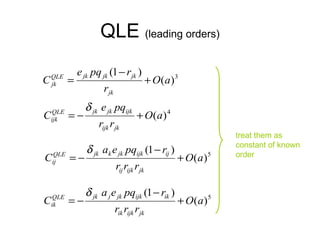
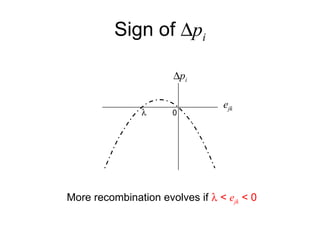
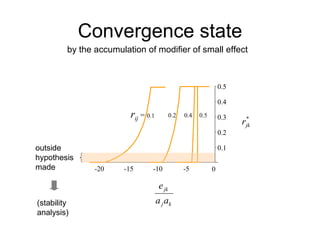
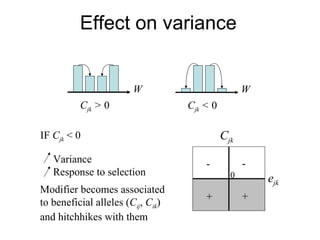
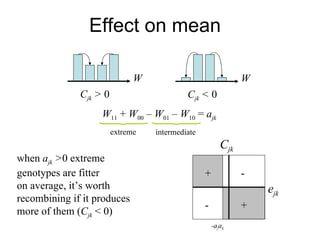
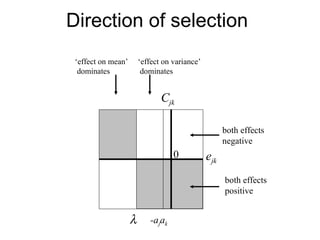
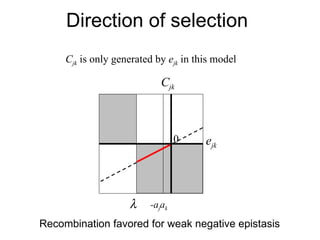
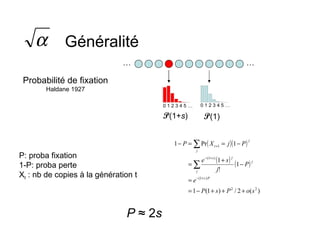
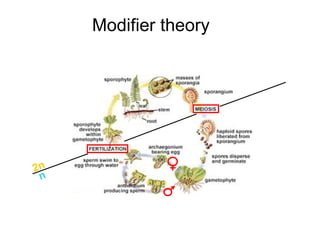
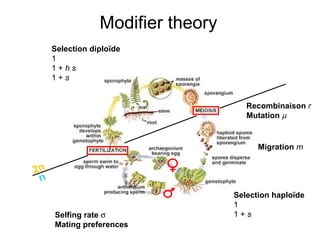
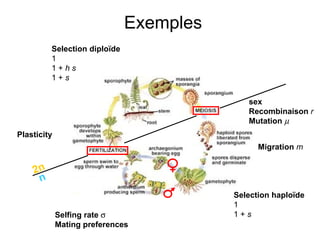
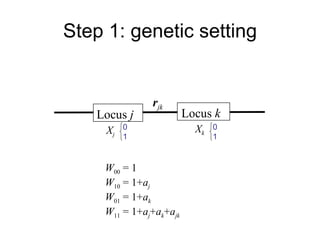
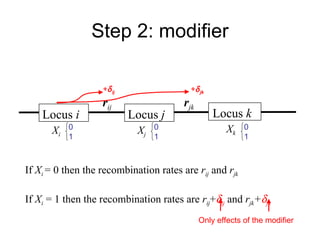
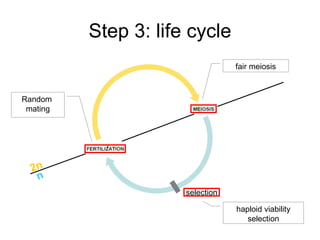
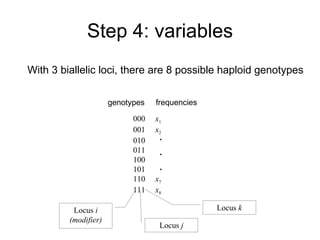
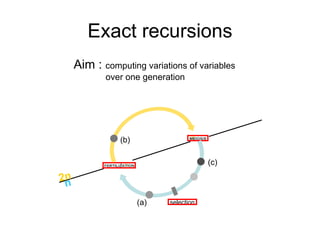
This document summarizes a population genetics model for studying the evolution of recombination rates. The model considers three loci, including a modifier locus that can alter the recombination rates between two selected loci. Using recursion equations and assumptions like weak epistasis and separation of timescales, the model analyzes when and why the frequency of a recombination-increasing allele at the modifier locus may increase over time through indirect selection. The key results are that more recombination evolves if epistasis between the selected loci is weakly negative and their association is negative.

1. Population genetics Thomas Lenormand CEFE – CNRS, Montpellier

2. The mathematics of frequency change An allele arise by mutation Its frequency change for several reasons Genome change ( = evolution occurs) Mendel + Darwin A ‘microscopic view’ founding other approaches

3. G P P G

4. (1892-1964) (1911-1998) (1890-1962) (1889-1988) (1920-2004) (1924-1994) (1916- ) (1929 - )

5. Levins 1966 Généralité Précision Réalisme Un corpus de modèles Theories - sexe - speciation - mort - altruisme Des Stats… bcp de stats - Mutations - Enzymes - Microsat - Sequences - Genomes

6. Réalisme distance x 0 1 0 2 0 4 0 6 0 {R} {E} fréquence

7. Précison Saccheri I J et al. PNAS 2008;105:16212-16217 1/(4π D e σ 2 )

8. Généralité Probabilité de fixation Haldane 1927 … … 0 1 2 3 4 5 … 0 1 2 3 4 5 … P (1+ s ) P (1) P: proba fixation 1-P: proba perte X t : nb de copies à la génération t P ≈ 2 s

9. Modifier theory 2n n

10. Selection diploïde 1 1 + h s 1 + s Selection haploïde 1 1 + s Recombinaison r Mutation  Selfing rate  Mating preferences Modifier theory Migration m 2n n

11. Modifier theory Suppose un locus qui modifie le caractère d’interet Regarde changement de fréquence d’un mutant Evolution à long terme du modifieur renseigne sur comment le caractère peut evoluer et dans quelles conditions Un modifieur peut évoluer - par sélection directe (naturelle, sexuelle, de parentèle) - par sélection indirecte On parle de modifieur « neutre » lorsqu’il n’y a que de la sélection indirecte Construire un modèle: combien de locus au minimum?

12. Selection diploïde 1 1 + h s 1 + s Selection haploïde 1 1 + s sex Recombinaison r Mutation  Selfing rate  Mating preferences Exemples Migration m Plasticity 2n n

13. Reduction principle If viability loci at stable polymorphic equilibrium Transmission evolves to be « perfect » ( r = 0,  = 0, m = 0, sex = 0) Selected loci are at equilibrium. Selection coefficients are constant. There is random mating. Only one transmission parameter is considered at a time. Viability is sex-independent. (Altenberg and Feldman 1987)

14. Modifier vs. optimality Does modifier evolve to maximise mean fitness ? Knowing what would be best for the pop does not say that evolution will lead there Modifiers are tools for modelling ‘ True’ genes have *always* pleiotropic effects

15. What is sex? 2n n

16. Why sex? What is the benefit of recombination? How to construct a model to measure this? Main hypothesis: sex allows for recombination

17. Part I Building the model from scratch Barton, N. H. 1995. A general model for the evolution of recombination. Genetical Research 65:123-144.

18. Key insights Recombination > 1 locus polymorphic otherwise uninteresting Simplest polymorphism mutation – haploid selection Keep it simple single population very large number of individuals (neglect drift)

19. Step 1: genetic setting Locus k Locus j r jk W 00 = 1 W 10 = 1+ a j W 01 = 1+ a k W 11 = 1+ a j + a k + a jk X j X k 0 1 0 1

20. Step 2: modifier Locus k Locus j r jk X j X k Locus i r ij X i If X i = 0 then the recombination rates are r ij and r jk If X i = 1 then the recombination rates are r ij +  ij and r jk +  jk Only effects of the modifier +  ij +  jk 0 1 0 1 0 1

21. Step 3: life cycle 2n n

22. Step 3: life cycle selection haploid viability selection fair meiosis Random mating 2n n

23. Step 4: variables With 3 biallelic loci, there are 8 possible haploid genotypes 000 x 1 001 x 2 010 011 100 101 110 x 7 111 x 8 . .. genotypes frequencies Locus i (modifier) Locus j Locus k

24. Step 4: variables frequencies 0 00 x 1 0 01 x 2 0 10 x 3 0 11 x 4 1 00 x 5 1 01 x 6 1 10 x 7 1 11 x 8

25. Step 4: variables frequencies 0 0 0 x 1 0 0 1 x 2 0 1 0 x 3 0 1 1 x 4 1 0 0 x 5 1 0 1 x 6 1 1 0 x 7 1 1 1 x 8

26. Step 4: variables Pairwise ‘associations’ 00 0 x 1 00 1 x 2 01 0 x 3 01 1 x 4 10 0 x 5 10 1 x 6 11 0 x 7 11 1 x 8 (usually referred to as ‘linkage disequilibrium’)

27. Step 4: variables triplet ‘association’ 000 x 1 001 x 2 010 x 3 011 x 4 100 x 5 101 x 6 110 x 7 111 x 8

28. Step 4: variables 000 x 1 001 x 2 010 x 3 011 x 4 100 x 5 101 x 6 110 x 7 111 x 8 Sum to 1 7 independent variables p i p j p k C ij C jk C ik C ijk 7 independent variables

29. Part II Writing the equations

30. Exact recursions Aim : computing variations of variables over one generation 2n n selection (a) (b) (c)

31. Step 1: selection

32. Step 2: Fertilization (random mating) Male gametes female gametes 000 001 010 011 100 101 110 111 000 x 1 2 001 x 1 x 2 x 2 2 010 x 1 x 3 x 2 x 3 x 3 2 011 … … … … 100 … … … … … 101 … … … … … … 110 … … … … … … … 111 … … … … … … x 7 x 8 x 8 2

33. Step 3: Meiosis Male gametes female gametes 001 010 001 010 000 011 (1- r jk )/2 (1- r jk )/2 r jk /2 r jk /2 Diploid individual produces gametes 000 001 010 011 100 101 110 111 000 x 1 2 001 x 1 x 2 x 2 2 010 x 1 x 3 x 2 x 3 x 3 2 011 … … … … 100 … … … … … 101 … … … … … … 110 … … … … … … … 111 … … … … … … x 7 x 8 x 8 2

34. Step 3: Meiosis Male gametes female gametes 101 110 001 010 000 011 (1- r jk -  )/2 (1- r jk -  )/2 ( r jk +  ) /2 Diploid individual produces gametes ( r jk +  ) /2 000 001 010 011 100 101 110 111 000 x 1 2 001 x 1 x 2 x 2 2 010 x 1 x 3 x 2 x 3 x 3 2 011 … … … … 100 … … … … … 101 … … … … … … 110 … … … … … … … 111 … … … … … … x 7 x 8 x 8 2

35. Exact recursions After mating meiosis mutation selection System of 7 independent equations g = 1…7

36. Changing variables equivalently recursions on

37. Part III Analyzing the model

38. Methods When does the allele at the modifier locus change in frequency? The exact recursions give the answer, but they are not helpful Dynamical system: equilibria? Analysis involve assumptions Method 1 : stability analysis Method 2 : separation of time scales

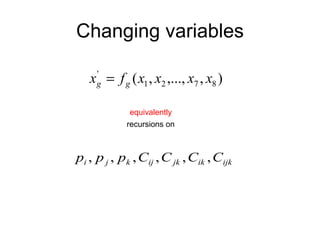
39. Taylor Series constant approximation linear approximation quadratic approximation Notation : Series[ f ( x ),{ x , x 0 , 2}] (like in Mathematica)

40. Assumptions r >> a p i changes at a even slower rate because indirect selection Associations change at a faster rate because r is larger p i p j p k C ij C jk C ik C ijk fast changing variables slow changing variables Separation of time scales = treat associations as constants also known as « Quasi Linkage Equilibrium » (QLE) p j and p k change slowly because a is small

41. Assumptions a j , a k >> a jk weak epistasis because more interesting (see later) W 00 = 1 W 10 = 1+ a j W 01 = 1+ a k W 11 = 1+ a j + a k + a jk W 00 = 1 W 10 = 1+ a j W 01 = 1+ a k W 11 = ( 1+ a j )(1+ a k )+ e jk a jk =e jk +a j a k  << r weak modifier effects investigate only evolution by the accumulation of small mutations

42. QLE C jk (association between the two selected loci) Association is generated by epistasis between the loci Recombination REDUCES associations

43. QLE (leading orders) treat them as constant of known order

44. Modifier where Final Result

45. Sign of  p i e jk  p i 0  More recombination evolves if  < e jk < 0

46. Convergence state -20 -15 -10 -5 0.1 0.2 0.3 0.4 0.5 r ij = 0.1 0.2 0.5 0.4 0 by the accumulation of modifier of small effect (stability analysis) outside hypothesis made

47. Part IV Interpreting the model

48. Back to equations Effect on the mean fitness of offspring Effect on the variance in fitness of offspring

49. Effect on variance Variance Response to selection + + - - Modifier becomes associated to beneficial alleles ( C ij , C ik ) and hitchhikes with them IF C jk < 0 W C jk > 0 W C jk < 0 e jk C jk 0

50. Effect on mean W 11 + W 00 – W 01 – W 10 = a jk when a jk > 0 extreme genotypes are fitter on average, it’s worth recombining if it produces more of them ( C jk < 0) e jk C jk -a j a k + + - - extreme intermediate W C jk > 0 W C jk < 0

51. Direction of selection e jk -a j a k C jk  0 both effects positive ‘ effect on mean’ dominates both effects negative ‘ effect on variance’ dominates

52. Direction of selection e jk -a j a k C jk  0 C jk is only generated by e jk in this model Recombination favored for weak negative epistasis

53. Part V Relate to other models

54. Fluctuating Epistasis (Barton 1995, Peters & Lively 1999) e jk C jk  0

55. Environmental heterogeneity (Lenormand & Otto 2000) e jk C jk  0 Cov( a j ,a k )>0 Cov( a j ,a k )<0

56. Hill-Robertson effect (originally Fisher 1930, Muller 1932) e jk C jk  0 Interference among selected loci generate negative C jk

57. Take home messages Recombination… is neutral in absence of associations can increase or decrease variance may increase variation but variation needs not be favourable can change both mean and variance in fitness frequency change depends on both the sign of genes associations and epistasis

58. Further? When to include stochasticity? Extending modifier theory to genome… Relationship to other approaches