The document covers fundamental concepts in vector calculus, including definitions of vectors and scalars, operations like addition, subtraction, and products (dot and cross), and applications such as integration and differentiation of vectors. Key topics include the del operator, line and surface integrals, and theorems like Green's and Stokes' theorem. Numerous examples and exercises are provided to illustrate the principles and calculations involved in vector analysis.

1. 1
Note on Vector Calculus
1. Elementary
2. Vector Product
3. Differentiation of Vectors
4. Integration of Vectors
5. Del Operator or Nabla (Symbol )
6. Polar Coordinates

2. 2
7. Line Integral
8. Volume Integral
9. Surface Integral
10. Green’s Theorem
11. Divergence Theorem (Gauss’ Theorem)
12. Stokes’ Theorem

3. 3
Elementary Vector Analysis
Definition (Scalar and vector)
Vector is a directed quantity, one with
both magnitude and direction.
For instance acceleration, velocity, force
Scalar is a quantity that has magnitude
but not direction.
For instance mass, volume, distance

4. 4
We represent a vector as an arrow from the
origin O to a point A.
The length of the arrow is the magnitude of
the vector written as or .
O
A
or
O
A
OA
a
a
OA

5. 5
Basic Vector System
Unit vectors , ,
• Perpendicular to each other
• In the positive directions
of the axes
• have magnitude (length) 1

6. 6
Define a basic vector system and form a
right-handed set, i.e

7. 7
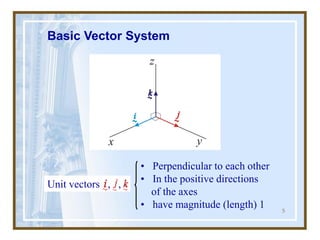
Magnitude of vectors
Let P = (x, y, z). Vector is defined by
with magnitude (length)
OP = = + +
p x i y j z k
= [ ]
x, y, z
OP = p
OP = = + +
p x y z
2 2 2

8. 8
Calculation of Vectors
1. Vector Equation
Two vectors are equal if and only if the
corresponding components are equals
3
3
2
2
1
1
3
2
1
3
2
1
,
,
Then
.
and
Let
b
a
b
a
b
a
b
a
k
b
j
b
i
b
b
k
a
j
a
i
a
a
=
=
=

=
+
+
=
+
+
=

9. 9
2. Addition and Subtraction of Vectors
3. Multiplication of Vectors by Scalars
k
b
a
j
b
a
i
b
a
b
a )
(
)
(
)
( 3
3
2
2
1
1 
+

+

=

k
b
j
b
i
b
b )
(
)
(
)
(
then
scalar,
a
is
If
3
2
1 




+
+
=

10. 10
Example 1
Given 5 3 and 4 3 2 . Find
p i j k q i j k
= + - = - +
a p q
) +
)
b p q
-
) 2 10
d q p
-
c p
) Magnitude of vector

11. 11
Vector Products
1 2 3 1 2 3
~ ~ ~ ~ ~ ~
~ ~
If and ,
a a i a j a k b b i b j b k
= + + = + +
1 1 2 2 3 3
~ ~
a b a b a b a b
 = + +
1) Scalar Product (Dot product)
2) Vector Product (Cross product)
     
~ ~
~
1 2 3
~ ~
1 2 3
2 3 3 2 1 3 3 1 1 2 2 1
~ ~
~
i j k
a b a a a
b b b
a b a b i a b a b j a b a b k
 =
= - - - + -
~
~
~
~
and
between
angle
the
is
,
cos
|
||
|
.
or b
a
b
a
b
a 

=

12. 12
3) Application of Multiplication of Vectors
a) Given 2 vectors and , projection onto
is defined by
b) The area of triangle
~ ~
1
.
2
A a b
= 
a b a b
a
b
b
a
compb a
|
|
|
.
|
)
(
length
|
|
.
comp
~
~
~
~
~
~
b
b
a
l
b
b
a
a
b
=
=

13. 13
c) The area of parallelogram
d) The volume of tetrahedrone
e) The volume of parallelepiped
a
b
a b
x
A =
a b
c
3
2
1
3
2
1
3
2
1
6
1
c
c
c
b
b
b
a
a
a
=
6
1
=
V a . b c
x
a b
c
3
2
1
3
2
1
3
2
1
c
c
c
b
b
b
a
a
a
=
=
V a . b c
x

14. 14
Example 2
.
and
between
angle
the
and
,
.
determine
,
2
and
3
2
Given
~
~
~
~
~
~
~
~
~
~
~
~
~
~
b
a
b
a
b
a
k
j
i
b
k
j
i
a

+
+
=
-
+
=

15. 15
Vector Differential Calculus
• Let A be a vector depending on parameter u,
• The derivative of A(u) is obtained by
differentiating each component separately,
~
~
~
~
k
du
da
j
du
da
i
du
da
du
A
d
z
y
x
+
+
=
~
~
~
~
)
(
)
(
)
(
)
( k
u
a
j
u
a
i
u
a
u
A z
y
x +
+
=

16. 16
• The nth derivative of vector is given by
• The magnitude of is
)
(
~
u
A
.
~
~
~
~
k
du
a
d
j
du
a
d
i
du
a
d
du
A
d
n
z
n
n
y
n
n
x
n
n
n
+
+
=
2
2
2
~








+








+








= n
z
n
n
y
n
n
x
n
n
n
du
a
d
du
a
d
du
a
d
du
A
d
n
n
du
A
d
~

17. 17
Example 3


=
=
+
-
=
2
~
2
~
~
~
~
2
~
hence
5
2
3
If
du
A
d
du
A
d
k
j
u
i
u
A

18. 18
Example 4
The position of a moving particle at time t is given
by x = 4t + 3, y = t2 + 3t, z = t3 + 5t2. Obtain
• The velocity and acceleration of the particle.
• The magnitude of both velocity and acceleration
at t = 1.

19. 19
Solution
• The parameter is t, and the position vector is
• The velocity is given by
• The acceleration is
.
)
5
(
)
3
(
)
3
4
(
)
(
~
2
3
~
2
~
~
k
t
t
j
t
t
i
t
t
r +
+
+
+
+
=
.
)
10
3
(
)
3
2
(
4
~
2
~
~
~
k
t
t
j
t
i
dt
r
d
+
+
+
+
=
.
)
10
6
(
2
~
~
2
~
2
k
t
j
dt
r
d
+
+
=

20. 20
• At t = 1, the velocity of the particle is
and the magnitude of the velocity is
.
13
5
4
))
1
(
10
)
1
(
3
(
)
3
)
1
(
2
(
4
)
1
(
~
~
~
~
2
~
~
~
k
j
i
k
j
i
dt
r
d
+
+
=
+
+
+
+
=
.
210
13
5
4
)
1
( 2
2
2
~
=
+
+
=
dt
r
d

21. 21
• At t = 1, the acceleration of the particle is
and the magnitude of the acceleration is
.
16
2
)
10
)
1
(
6
(
2
)
1
(
~
~
~
~
2
~
2
k
j
k
j
dt
r
d
+
=
+
+
=
.
65
2
16
2
)
1
( 2
2
2
~
2
=
+
=
dt
r
d

22. 22
Differentiation of Two Vectors
If both and are vectors, then
)
(
~
u
A )
(
~
u
B
~
~
~
~
~
~
~
~
~
~
~
~
~
~
~
~
~
~
)
(
)
.
.
)
.
(
)
)
(
)
)
(
)
B
du
A
d
du
B
d
A
B
A
du
d
d
B
du
A
d
du
B
d
A
B
A
du
d
c
du
B
d
du
A
d
B
A
du
d
b
du
A
d
c
A
c
du
d
a

+

=

+
=
+
=
+
=

23. 23
Partial Derivatives of a Vector
• If vector depends on more than one
parameter, i.e
~
A
~
2
1
~
2
1
~
2
1
2
1
~
)
,
,
,
(
)
,
,
,
(
)
,
,
,
(
)
,
,
,
(
k
u
u
u
a
j
u
u
u
a
i
u
u
u
a
u
u
u
A
n
z
n
y
n
x
n




+
+
=

24. 24
• Partial derivative of with respect to is
given by
e.t.c.
~
A
~
2
1
2
~
2
1
2
~
2
1
2
2
1
~
2
~
1
~
1
~
1
1
~
,
k
u
u
a
j
u
u
a
i
u
u
a
u
u
A
k
u
a
j
u
a
i
u
a
u
A
z
y
x
z
y
x



+



+



=





+


+


=


1
u

25. 25
Example 5
~
~
2
~
2
~
~
2
~
2
~
~
2
~
2
~
~
~
~
~
2
~
~
2
~
~
2
3
~
2
~
2
~
6
,
2
6
,
6
4
,
2
6
,
3
4
3
then
)
(
)
2
(
3
If
i
v
u
v
F
v
u
F
k
i
u
v
F
k
u
j
u
F
k
v
j
i
uv
v
F
k
u
j
u
i
v
u
F
k
v
u
j
v
u
i
uv
F
=



=



+
=


+
=


+
-
=


+
+
=


+
+
-
+
=

26. 26
Exercise 1






=



=



=


=


=


=


+
+
-
+
=
u
v
F
v
u
F
v
F
u
F
v
F
u
F
k
v
u
j
v
u
i
v
u
F
~
2
~
2
2
~
2
2
~
2
~
~
~
2
3
~
3
~
2
~
,
,
,
then
)
3
(
)
3
(
2
If

27. 27
Vector Integral Calculus
• The concept of vector integral is the same as
the integral of real-valued functions except
that the result of vector integral is a vector.
.
)
(
)
(
)
(
)
(
then
)
(
)
(
)
(
)
(
If
~
~
~
~
~
~
~
~
k
du
u
a
j
du
u
a
i
du
u
a
du
u
A
k
u
a
j
u
a
i
u
a
u
A
b
a
z
b
a
y
b
a
x
b
a
z
y
x




+
+
=
+
+
=

28. 28
Example 6
.
80
2
42
]
[
]
5
[
]
2
[
4
)
5
2
(
)
4
3
(
.
calculate
,
4
)
5
2
(
)
4
3
(
If
~
~
~
~
3
1
4
~
3
1
2
~
3
1
2
3
3
1 ~
3
3
1 ~
3
1 ~
2
3
1 ~
3
1 ~
~
3
~
~
2
~
k
j
i
k
t
j
t
t
i
t
t
k
dt
t
j
dt
t
i
dt
t
t
dt
F
dt
F
k
t
j
t
i
t
t
F
+
-
=
+
-
+
+
=
+
-
+
+
=
+
-
+
+
=





Answer

29. 29
Exercise 2
.
2
7
3
2
4
7
)
4
(
2
)
3
(
.
calculate
,
)
4
(
2
)
3
(
If
~
~
~
1
0 ~
1
0 ~
2
1
0 ~
3
1
0 ~
1
0 ~
~
~
2
~
3
~
k
j
i
k
dt
t
j
dt
t
i
dt
t
t
dt
F
dt
F
k
t
j
t
i
t
t
F
-
+
=
=
=
-
+
+
+
=
-
+
+
+
=







Answer

30. 30
Del Operator Or Nabla (Symbol )
• Operator  is called vector differential operator,
defined as
.
~
~
~ 









+


+


=
 k
z
j
y
i
x

31. 31
Grad (Gradient of Scalar Functions)
• If  x,y,z is a scalar function of three variables
and  is differentiable, the gradient of  is
defined as
.
grad
~
~
~
k
z
j
y
i
x 

+


+


=

=





function
vector
a
is
*
function
scalar
a
is
*




32. 32
Example 7
z
xy
yz
x
xyz
z
x
z
y
xyz
z
xy
yz
x
z
xy
yz
x
2
2
2
2
3
2
2
2
3
2
2
3
2
2
2
3
2
2
3
z
2
y
2
x
hence
,
Given
(1,3,2).
P
at
grad
determine
,
If
+
=


+
=


+
=


+
=
=
+
=






Solution

33. 33
.
72
32
84
.
))
2
(
)
3
)(
1
(
2
)
2
)(
3
(
)
1
(
3
(
)
)
2
)(
3
)(
1
(
2
)
2
(
)
1
((
)
)
2
(
)
3
(
)
2
)(
3
)(
1
(
2
(
have
we
(1,3,2),
P
At
.
)
2
3
(
)
2
(
)
2
(
z
y
x
Therefore,
~
~
~
~
2
2
2
~
2
3
2
~
2
2
3
~
2
2
2
~
2
3
2
~
2
2
3
~
~
~
k
j
i
k
j
i
k
z
xy
yz
x
j
xyz
z
x
i
z
y
xyz
k
j
i
+
+
=
+
+
+
+
+
=

=
+
+
+
+
+
=


+


+


=







34. 34
Exercise 3
(1,2,3).
P
point
at
grad
determine
,
If 3
2
3
=
+
=

 z
xy
yz
x

35. 35
Solution
.
110
111
126
(1,2,3),
P
At
Grad
z
y
x
then
,
Given
~
~
~
3
2
3
k
j
i
z
xy
yz
x
+
+
=

=
=

=

=


=


=


+
=












36. 36
Grad Properties
If A and B are two scalars, then
)
(
)
(
)
(
)
2
)
(
)
1
A
B
B
A
AB
B
A
B
A

+

=


+

=
+


37. 37
Directional Derivative
.
of
direction
in the
r
unit vecto
a
is
which
,
where
.
is
of
direction
in the
of
derivative
l
Directiona
~
~
~
~
~
~
r
d
r
d
r
d
a
grad
a
ds
d
a
=
= 



38. 38
Example 8
.
4
3
2
vector
the
of
direction
in the
)
1
,
2
,
1
(
point
at the
2
of
derivative
l
directiona
the
Compute
~
~
~
~
2
2
2
k
j
i
A
yz
xy
z
x
-
+
=
-
+
+
=


39. 39
Solution
Directional derivative of  in the direction of
.
)
2
(
)
4
(
)
2
2
(
hence
,
2
Given
~
2
~
2
~
2
2
2
2
k
yz
x
j
z
xy
i
y
xz
yz
xy
z
x
+
+
+
+
+
=

+
+
=


.
and
where
.
~
~
~
~
~
~
~
A
A
a
k
z
j
y
i
x
grad
grad
a
ds
d
=


+


+


=

=
=







~
a

40. 40
.
29
)
4
(
3
2
then
,
4
3
2
given
Also,
.
3
9
6
.
))
1
)(
2
(
2
)
1
((
)
)
1
(
)
2
)(
1
(
4
(
)
)
2
(
2
)
1
)(
1
(
2
(
(1,2,-1),
At
2
2
2
~
~
~
~
~
~
~
~
~
2
~
2
~
2
=
-
+
+
=
-
+
=
-
+
=
-
+
+
-
+
+
+
-
=

A
k
j
i
A
k
j
i
k
j
i


41. 41
.
470462
.
9
29
51
)
3
(
29
4
)
9
(
29
3
)
6
(
29
2
)
3
9
6
.(
29
4
29
3
29
2
.
Then,
.
29
4
29
3
29
2
Therefore,
~
~
~
~
~
~
~
~
~
~
~
~
~

=
-






-
+






+






=
-
+






-
+
=

=
-
+
=
=
k
j
i
k
j
i
a
ds
dφ
k
j
i
A
A
a


42. 42
Unit Normal Vector
Equation  (x, y, z) = constant is a surface
equation. Since  (x, y, z) = constant, the derivative
of  is zero; i.e.
.
90
0
cos
0
cos
grad
0
grad
.
~
~

=

=

=

=
=






r
d
r
d
d

43. 43
• This shows that when  (x, y, z) = constant,
• Vector grad  =   is called normal vector to the
surface  (x, y, z) = constant
.
~
r
d
grad 

y
ds
grad 
z
x

44. 44
Unit normal vector is denoted by
Example 9
Calculate the unit normal vector at (-1,1,1)
for 2yz + xz + xy = 0.
.
~ 



=
n

45. 45
Solution
Given 2yz + xz + xy = 0. Thus
.
6
1
1
4
and
2
)
1
2
(
)
1
2
(
)
1
1
(
(-1,1,1),
At
.
)
2
(
)
2
(
)
(
~
~
~
~
~
~
~
~
~
=
+
+
=

+
+
=
-
+
-
+
+
=

+
+
+
+
+
=




k
j
i
k
j
i
k
x
y
j
x
z
i
y
z
)
2
(
6
1
6
2
is
vector
normal
unit
The
~
~
~
~
~
~
k
j
i
k
j
i
n
~
+
+
=
+
+
=


=




46. 46
Divergence of a Vector
.
.
)
.(
.
as
defined
is
of
divergence
the
,
If
~
~
~
~
~
~
~
~
~
~
~
~
~
~
~
z
a
y
a
x
a
A
A
div
k
a
j
a
i
a
k
z
j
y
i
x
A
A
div
A
k
a
j
a
i
a
A
z
y
x
z
y
x
z
y
x


+


+


=

=

+
+










+


+


=

=
+
+
=

47. 47
Example 10
.
13
)
3
)(
2
(
2
)
3
)(
1
(
)
2
)(
1
(
2
(1,2,3),
point
At
.
2
2
.
(1,2,3).
point
at
determine
,
If
~
~
~
~
~
2
~
~
2
~
=
+
-
=
+
-
=


+


+


=

=
+
-
=
A
div
yz
xz
xy
z
a
y
a
x
a
A
A
div
A
div
k
yz
j
xyz
i
y
x
A
z
y
x
Answer

48. 48
Exercise 4
.
114
(3,2,1),
point
At
.
(3,2,1).
point
at
determine
,
If
~
~
~
~
~
3
~
2
~
2
3
~
=
=
=


+


+


=

=
-
+
=


A
div
z
a
y
a
x
a
A
A
div
A
div
k
yz
j
z
xy
i
y
x
A
z
y
x
Answer

49. 49
Remarks
.
called
is
vector
,
0
If
function.
scalar
a
is
but
function,
vector
a
is
~
~
~
~
vector
solenoid
A
A
div
A
div
A
=

50. 50
Curl of a Vector
.
)
(
by
defined
is
of
curl
the
,
If
~
~
~
~
~
~
~
~
~
~
~
~
~
~
~
~
~
~
z
y
x
z
y
x
z
y
x
a
a
a
z
y
x
k
j
i
A
A
curl
k
a
j
a
i
a
k
z
j
y
i
x
A
A
curl
A
k
a
j
a
i
a
A






=


=

+
+











+


+


=


=
+
+
=

51. 51
Example 11
.
)
2
,
3
,
1
(
at
determine
,
)
(
)
(
If
~
~
2
~
2
2
~
2
2
4
~
-
-
+
+
-
=
A
curl
k
yz
x
j
y
x
i
z
x
y
A

52. 52
Solution
.
)
4
2
(
)
2
2
(
)
(
)
(
)
(
)
(
)
(
)
(
~
3
~
2
~
2
~
2
2
4
2
2
~
2
2
4
2
~
2
2
2
2
2
2
2
2
4
~
~
~
~
~
k
y
x
j
z
x
xyz
i
z
x
k
z
x
y
y
y
x
x
j
z
x
y
z
yz
x
x
i
y
x
z
yz
x
y
yz
x
y
x
z
x
y
z
y
x
k
j
i
A
A
curl
-
+
+
-
-
-
=








-


-
+


+






-


-
-


-








+


-
-


=
-
+
-






=


=

53. 53
.
106
8
2
)
)
3
(
4
)
1
(
2
(
))
2
(
)
1
(
2
)
2
)(
3
)(
1
(
2
(
)
2
(
)
1
(
(1,3,-2),
At
~
~
~
~
3
~
2
~
2
~
k
j
i
k
j
i
A
curl
-
-
=
-
+
-
+
-
-
-
-
-
=
Exercise 5
.
)
3
,
2
,
1
(
point
at
determine
,
)
(
)
(
If
~
~
2
2
~
2
2
~
2
2
3
~
A
curl
k
yz
x
j
z
x
i
z
y
xy
A -
+
+
-
=

54. 54
Answer
.
26
12
15
(1,2,3),
At
.
)
2
3
2
(
)
2
2
(
)
2
(
~
~
~
~
~
2
2
~
2
2
~
2
2
~
k
j
i
A
curl
k
yz
xy
x
j
z
y
xyz
i
z
z
x
A
curl
+
+
-
=
+
-
+
+
-
-
-
-
=
Remark
function.
vector
a
also
is
and
function
vector
a
is
~
~
A
curl
A

55. 55
Polar Coordinates
• Polar coordinate is used in calculus to
calculate an area and volume of small
elements in easy way.
• Lets look at 3 situations where des Cartes
Coordinate can be rewritten in the form of
Polar coordinate.

56. 56
Polar Coordinate for Plane (r, θ)
x
ds
y

d



d
dr
r
dS
r
y
r
x
=
=
=
sin
cos

57. 57
Polar Coordinate for Cylinder ( ,, z)
dz
d
d
dV
dz
d
dS
z
z
y
x









=
=
=
=
=
sin
cos

x
y
z
dv

z
ds

58. 58
Polar Coordinate for Sphere (r,  ,











d
d
dr
r
dV
d
d
r
dS
r
z
r
y
r
x
sin
sin
cos
sin
sin
cos
sin
2
2
=
=
=
=
=
y
x
r
z



59. 59
Example (Volume Integral)
.
9
and
4
,
0
by
bounded
space
a
is
and
2
2
where
Calculate
2
2
~
~
~
~
~
=
+
=
=
+
+
=

y
x
z
z
V
k
y
j
z
i
F
dV
F
V
x
z

y

4 -
3
3

60. 60
Solution
Since it is about a cylinder, it is easier if we use
cylindrical polar coordinates, where
.
4
0
,
2
0
,
3
0
where
,
,
sin
,
cos






=
=
=
=
z
dz
d
d
dV
z
z
y
x











61. 61
Line Integral
Ordinary integral  f (x) dx, we integrate along
the x-axis. But for line integral, the integration is
along a curve.
 f (s) ds =  f (x, y, z) ds
A
O
B
~
~
r
d
r+
~
r

62. 62
Scalar Field, V Integral
If there exists a scalar field V along a curve C,
then the line integral of V along C is defined by
.
where
~
~
~
~
~
k
dz
j
dy
i
dx
r
d
r
d
V
c
+
+
=


63. 63
Example
(3,2,1).
B
to
(0,0,0)
A
from
along
find
then
,
,
2
,
3
by
given
is
curve
a
and
z
If
~
3
2
2
=
=
=
=
=
=
 C
r
d
V
u
z
u
y
u
x
C
xy
V
c

64. 64
Solution
.
1
,
1
,
2
2
,
3
3
(3,2,1),
B
At
.
0
,
0
,
0
2
,
0
3
(0,0,0),
A
At
.
3
4
3
And,
.
12
)
(
)
2
)(
3
(
z
Given
3
2
3
2
~
2
~
~
~
~
~
~
8
3
2
2
2
=

=
=
=
=
=

=
=
=
=
+
+
=
+
+
=
=
=
=
u
u
u
u
u
u
u
u
k
du
u
j
du
u
i
du
k
dz
j
dy
i
dx
r
d
u
u
u
u
xy
V

65. 65
 
.
11
36
5
24
4
11
36
5
24
4
36
48
36
)
3
4
3
)(
12
(
~
~
~
~
1
0
11
~
1
0
10
~
1
0
9
1
0 ~
10
1
0
~
9
1
0
~
8
1
0 ~
2
~
~
8
~
k
j
i
k
u
j
u
i
u
k
du
u
j
du
u
i
du
u
k
du
u
j
udu
i
du
u
r
d
V
u
u
B
A
+
+
=






+






+
=
+
+
=
+
+
=

 



=
=

66. 66
Exercise
.
11
768
144
5
384
(4,3,2).
B
to
(0,0,0)
A
from
curve
the
along
calculate
,
2
,
3
,
4
by
given
is
curve
the
and
If
~
~
~
~
~
2
3
2
2
k
j
i
r
d
V
C
r
d
V
u
z
u
y
u
x
C
yz
x
V
B
A
c
+
+
=
=
=
=
=
=
=


Answer

67. 67
Vector Field, Integral
Let a vector field
and
The scalar product is written as
.
)
).(
(
.
~
~
~
~
~
~
~
~
dz
F
dy
F
dx
F
k
dz
j
dy
i
dx
k
F
j
F
i
F
r
d
F
z
y
x
z
y
x
+
+
=
+
+
+
+
=
~
F
~
~
~
~
k
F
j
F
i
F
F z
y
x +
+
=
.
~
~
~
~
k
dz
j
dy
i
dx
r
d +
+
=
~
~
. r
d
F

68. 68
.
.
by
given
is
B
point
another
A to
point
a
from
curve
the
along
of
integral
line
then the
,
curve
the
along
is
field
vector
a
If
~
~
~
~



 +
+
=
c
z
c
y
c
x
c
dz
F
dy
F
dx
F
r
d
F
C
F
C
F

69. 69
Example
.
y
2
y
if
,
2
,
4
curve
the
along
(4,2,1)
B
to
(0,0,0)
A
from
.
Calculate
~
~
~
2
~
3
2
~
~
k
z
j
xz
i
x
F
t
z
t
y
t
x
r
d
F
c
-
+
=
=
=
=
=
=


70. 70
Solution
.
3
4
4
And
.
4
4
32
)
(
)
2
(
2
)
(
)
4
(
)
2
(
)
4
(
2
y
Given
~
2
~
~
~
~
~
~
~
5
~
4
~
4
~
3
2
~
3
~
2
2
~
~
~
2
~
k
dt
t
j
dt
t
i
dt
k
dz
j
dy
i
dx
r
d
k
t
j
t
i
t
k
t
t
j
t
t
i
t
t
k
yz
j
xz
i
x
F
+
+
=
+
+
=
-
+
=
-
+
=
-
+
=

71. 71
.
)
12
16
128
(
12
16
128
)
3
)(
4
(
)
4
)(
4
(
)
4
)(
32
(
)
3
4
4
)(
4
4
32
(
.
Then
7
5
4
7
5
4
2
5
4
4
~
2
~
~
~
5
~
4
~
4
~
~
dt
t
t
t
dt
t
dt
t
dt
t
dt
t
t
tdt
t
dt
t
k
dt
t
j
dt
t
i
dt
k
t
j
t
i
t
r
d
F
-
+
=
-
+
=
-
+
+
=
+
+
-
+
=
.
1
,
1
,
2
2
,
4
4
(4,2,1),
B
at
and,
.
0
,
0
,
0
2
,
0
4
(0,0,0),
A
At
3
2
3
2
=

=
=
=
=
=

=
=
=
=
t
t
t
t
t
t
t
t

72. 72
.
30
23
26
2
3
3
8
5
128
2
3
3
8
5
128
)
12
16
128
(
.
1
0
8
6
5
1
0
7
5
4
~
~
=
-
+
=






-
+
=
-
+
=
 

=
=
t
t
t
dt
t
t
t
r
d
F
t
t
B
A

73. 73
Exercise
.
168
61
7
.
.
3
,
2
,
curve
on the
(1,2,3)
B
to
(0,0,0)
A
from
.
calculate
,
3
If
~
~
3
2
~
~
~
2
~
~
2
~
=
=
=
=
=
=
+
-
=


r
d
F
t
z
t
y
t
x
r
d
F
k
z
x
j
yz
i
xy
F
B
A
c
Answer

74. 78
Volume Integral
Scalar Field, F Integral
If V is a closed region and F is a scalar field in
region V, volume integral F of V is

 =
V
V
Fdxdydz
FdV

75. 79
Example
Scalar function F = 2 x defeated in one cubic that
has been built by planes x = 0, x = 1, y = 0, y = 3,
z = 0 and z = 2. Evaluate volume integral F of the
cubic.
z
x
y
3
O
2
1

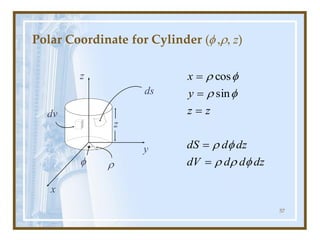
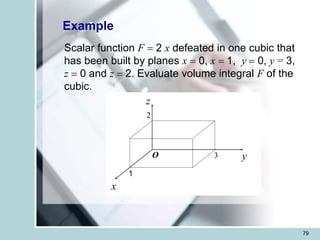
76. 80
  
 = = =
=
2
0
3
0
1
0
2
z y x
V
xdxdydz
FdV
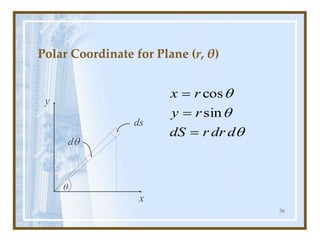
Solution
6
]
[
3
3
]
[
2
1
.
2
2
1
2
2
2
2
0
2
0
3
0
2
0
2
0
3
0
1
0
2
0
3
0
2
=
=
=
=
=






=


 
 
=
=
= =
= =
z
dz
dz
y
dydz
dydz
x
z
z
z y
z y

77. 81
Vector Field, Integral
~
F
If V is a closed region and , vector field in region
V, Volume integral of V is
~
F
~
F
   
=
V
x
x
y
y
z
z
dzdydx
F
dV
F
2
1
2
1
2
1 ~
~

78. 82
, where V is a region bounded by
x = 0, y = 0, z = 0 and 2x + y + z = 2, and also
given
V
dV
F
~
~
~
~
2 k
y
i
z
F +
=
Example
Evaluate

79. 83
If x = y = 0, plane 2x + y + z = 2 intersects z-axis at z = 2.
(0,0,2)
If x = z = 0, plane 2x + y + z = 2 intersects y-axis at y = 2.
(0,2,0)
If y = z = 0, plane 2x + y + z = 2 intersects x-axis at x = 1.
(1,0,0)
Solution

80. 84
We can generate this integral in 3 steps :
1. Line Integral from x = 0 to x = 1.
2. Surface Integral from line y = 0 to line y = 2(1-x).
3. Volume Integral from surface z = 0 to surface
2x + y + z = 2 that is z = 2 (1-x) - y
z
x
y
2
O
2
1
2x + y + z = 2
y = 2 (1 - x)

81. 85
Therefore,
   
=
-
=
-
-
=
=
V x
x
y
y
x
z
dzdydx
F
dV
F
1
0
)
1
(
2
0
)
1
(
2
0 ~
~
 

-
=
-
-
=
=
+
=
)
1
(
2
0
)
1
(
2
0 ~
~
1
0
)
2
(
x
y
y
x
z
x
dzdydx
k
y
i
z
~
~ 3
1
3
2
k
i+
=



82. 86
Example
Evaluate where
and V is region bounded by z = 0, z = 4 and
x2 + y2 = 9
V
dV
F
~ ~
~
~
~
2
2 k
y
j
z
i
F +
+
=
x
z

y

4 -
3
3

83. 87

 cos
=
x 
 sin
=
y z
z =
z
d
ρdρd
dV 
=
; ; ;
where
,
3
0 
  ,
2
0 
 
 4
0 
 z
Using polar coordinate of cylinder,

84. 88
  +
+
=
V V
dxdydz
k
y
j
z
i
dV
F )
2
2
(
~
~
~
~
Therefore,
  
= = =
+
+
=
4
0
2
0
3
0 ~
~
~
)
sin
2
2
(
z
k
j
z
i

 


 dz
d
d 

~
~
144
72 j
i 
 +
=



85. 89
Exercise

86. 90
Surface Integral
Scalar Field, V Integral
If scalar field V exists on surface S, surface
integral V of S is defined by
 
=
S S
dS
n
V
S
Vd
~
~
where
S
S
n


=
~

87. 91
Example
Scalar field V = x y z defeated on the surface
S : x2 + y2 = 4 between z = 0 and z = 3 in the
first octant.
Evaluate
S
S
Vd
~
Solution
Given S : x2 + y2 = 4 , so grad S is
~
~
~
~
~
2
2 j
y
i
x
k
z
S
j
y
S
i
x
S
S +
=


+


+


=


88. 92
Also,
4
4
2
2
)
2
(
)
2
( 2
2
2
2
=
=
+
=
+
=
 y
x
y
x
S
Therefore,
)
(
2
1
4
2
2
~
~
~
~
~
j
y
i
x
j
y
i
x
S
S
n +
=
+
=


=
Then,
  +






=
S S
dS
j
y
i
x
xyz
dS
n
V )
(
2
1
~
~
~
 +
= dS
j
z
xy
i
yz
x )
(
2
1
~
2
~
2

89. 93
Surface S : x2 + y2 = 4 is bounded by z = 0 and z = 3
that is a cylinder with z-axis as a cylinder axes and
radius,
So, we will use polar coordinate of cylinder to find
the surface integral.
.
2
4 =
=

x
z

y
2
2
3
O

90. 94
Polar Coordinate for Cylinder
cos 2cos
sin 2sin
ρ
x
y
z z
dS d dz
  
  

= =
= =
=
=
where
2
0

 
 3
0 
 z
(1st octant) and

91. 95
Using polar coordinate of cylinder,








cos
sin
8
)
(
)
sin
2
)(
cos
2
(
sin
cos
8
)
sin
2
(
)
cos
2
(
2
2
2
2
2
2
z
z
z
xy
z
z
yz
x
=
=
=
=
From


 =
+
=
S
S
S
S
Vd
dS
j
z
xy
i
yz
x
dS
n
V
~
~
2
~
2
~
)
(
2
1

92. 96
  
= =
+
=
S
z
dzd
j
z
i
z
S
Vd 2
0
3
0 ~
2
~
2
~
)
2
)(
cos
sin
8
sin
cos
8
(
2
1 






3
2 2 2 2
2
0 ~ ~ 0
2 2
2
0 ~ ~
1 1
8 cos sin sin cos
2 2
9 9
8 cos sin sin cos
2 2
z i z j d
i j d


    
    
 
= +
 
 
 
= +
 
 


2 2
2
0 ~ ~
3 3 2
~ ~
0
~ ~
9
8 cos sin sin cos
2
cos sin sin cos
36
3( sin ) 3(cos )
12( )
i j d
i j
i j


    
   
 
 
=  +
 
 
 
= +
 
-
 
= +

Therefore,

93. 97
2
2 2
~
,
9
0 2
S
If V is a scalar field whereV xyz evaluate
V d S for surface S that region bounded by x y
between z and z in the first octant.
=
+ =
= =

Exercise
~ ~
: 24( )
Answer i j
+

94. 98
Vector Field, Integral
If vector field defeated on surface S, surface
integral of S is defined as

 =
S
S
dS
n
F
S
d
F .
.
~
~
~
~
~
F
~
F
~
F
~
where
S
n
S

=


95. 99
Example
~ ~ ~
~
2 2 2
~ ~
Vector field 2 defeated on surface
: 9 and bounded by 0, 0, 0 in
the first octant.
Evaluate . .
S
F y i j k
S x y z x y z
F d S
= + +
+ + = = = =


96. 100
Solution
2 2 2
Given : 9 is bounded by 0, 0,
0 in the1st octant. This refer to sphere with center
at (0,0,0) and radius, 3, in the1st octant.
S x y z x y
z
r
+ + = = =
=
=
x
z
y
3
3
3
O

97. 101
~ ~
~
~ ~
~
2 2 2
2 2 2
So, grad is
2 2 2 ,
and
(2 ) (2 ) (2 )
2
2 9 6.
S
S S S
S i j k
x y z
x i y j z k
S x y z
x y z
  
 = + +
  
= + +
 = + +
= + +
= =

98. 102
~ ~
~ ~
~ ~ ~ ~
~ ~
Therefore,
. .
1
( 2 ) ( )
3
1
( 2 ) .
3
S S
S
S
F d S F ndS
y i j k x i y j z k dS
xy y z dS
=
 
= + + + +
 
 
= + +
 


).
(
3
1
6
2
2
2
~
~
~
~
~
~
~
k
z
j
y
i
x
k
z
j
y
i
x
S
S
n
+
+
=
+
+
=


=


99. 103
Using polar coordinate of sphere,
2
sin cos 3sin cos
sin sin 3sin sin
cos 3cos
sin 9sin
where 0 , .
2
x r
y r
z r
dS r d d d d
   
   
 
     

 
= =
= =
= =
= =
 

100. 104



















 
 
 
 
d
d
d
d
S
d
F
S
]
cos
sin
sin
sin
2
cos
sin
sin
3
[
9
]
sin
9
[
]
cos
3
)
sin
sin
3
(
2
)
sin
sin
3
)(
cos
sin
3
[(
3
1
.
2
0 0
3
0 0
~
~
2 2
2 2
+
+
=
+
+
=

 
  
= =
= =






+
=
4
3
1
9




101. 105
Exercise
octant.
1
in the
0
and
0
,
0
,
4
by
bounded
region
the
of
surface
a
is
and
2
where
,
on
Evaluate
st
2
2
2
~
~
~
~
~
~
=
=
=
=
+
+
+
+
=


z
y
x
z
y
x
S
k
y
j
z
i
x
F
S
S
d
F
S
:8 1
6
Answer

 
+
 
 

102. 106
Green’s Theorem
If c is a closed curve in counter-clockwise on
plane-xy, and given two functions P(x, y) and
Q(x, y),
where S is the area of c.

 +
=










-


c
S
dy
Q
dx
P
dy
dx
y
P
x
Q
)
(

103. 107
Example
2 2
2 2
Prove Green's Theorem for
[( ) ( 2 ) ]
which has been evaluated by boundary that defined as
0, 0 4 in the first quarter.
c
x y dx x y dy
x y and x y
+ + +
= = + =

y
2
x
2
C3
C2
C1
O
x2 + y2 = 22
Solution

104. 108
1 1
2 2
2 2
1 2 3
1
2 2
2
2
0
2
3
0
Given [( ) ( 2 ) ] where
and 2 . We defined curve
as , .
i) For : 0, 0 0 2
( ) ( ) ( 2 )
1 8
.
3 3
c
c c
x y dx x y dy
P x y Q x y c
c c and c
c y dy and x
Pdx Qdy x y dx x y dy
x dx
x
+ + +
= + = +
= =  
 
+ = + + +
 
=
 
= =
 
 

 


105. 109
2 2
2
ii) For : 4 ,in the first quarter from (2,0) to (0,2).
This curve actually a part of a circle.
Therefore, it's more easier if we integrate by using polar
coordinate of plane,
2cos , 2sin , 0
c x y
x y
 
+ =
= =
2
2sin , 2cos .
dx d dy d


   
 
 = - =

106. 110
 
 
.
4
4
8
sin
4
2
sin
2
cos
8
)
cos
sin
8
2
cos
2
2
sin
8
(
)
cos
sin
8
cos
4
sin
8
(
)]
cos
2
))(
sin
2
(
2
cos
2
((
)
sin
2
)(
)
sin
2
(
)
cos
2
((
[
)
2
(
)
(
)
(
2
2
2
2
2
2
0
2
0
0
2
2
2
0
2
2
-
=
+
+
-
=
+
+
+
=
+
+
+
-
=
+
+
-
=
+
+
-
+
=
+
+
+
=
+

































d
d
d
d
dy
y
x
dx
y
x
Qdy
Pdx
c
c

107. 111
3 3
3
2 2
0
2
0
2
2
iii) : 0, 0, 0 2
( ) ( ) ( 2 )
2
4.
8 16
( ) ( 4) 4 .
3 3
c c
c
For c x dx y
Pdx Qdy x y dx x y dy
y dy
y
Pdx Qdy  
= =  
 
+ = + + +
 
=
 
=  
= -
 + = + - - = -
 



108. 112
b) Now, we evaluate
where 1 2 .
Again,because this is a part of the circle,
we shall integrate by using polar coordinate of plane,
cos , sin
where
S
Q P
dxdy
x y
Q P
and y
x y
x r y r
 
 
 
-
 
 
 
 
= =
 
= =

0 r 2, 0 .
2
and dxdy dS r dr d

 
    = =

109. 113
.
3
16
cos
3
16
2
sin
3
16
2
sin
3
2
2
1
)
sin
2
1
(
)
2
1
(
2
2
2
2
0
0
2
0
0
3
2
0
2
0
-
=






+
=






-
=






-
=
-
=
-
=










-




 


=
=
= =
















d
d
r
r
d
dr
r
r
dy
dx
y
dy
dx
y
P
x
Q
r
S
S

110. 114
Therefore,
( )
16
.
3
Green's Theorem has been proved.
C S
Q P
Pdx Qdy dxdy
x y
LHS RHS

 
 
+ = -
 
 
 
= -
=

 

111. 115
Divergence Theorem (Gauss’ Theorem)
If S is a closed surface including region V in
vector field
.
.
~
~
~ 
 =
S
V
S
d
F
dV
F
div
~
F
~
y
x z
f
f f
div F
x y z

 
= + +
  

112. 116
Example
2
~ ~ ~
~
2 2
Prove Gauss' Theorem for vector field,
2 in the region bounded by
planes 0, 4, 0, 0 4
in the first octant.
F x i j z k
z z x y and x y
= + +
= = = = + =

113. 117
Solution
x
z
y
2
2
4
O
S3
S4
S2
S1
S5

114. 118
1
2
3
4
2 2
5
~
~ ~
For this problem, the region of integration is bounded
by 5 planes :
: 0
: 4
: 0
: 0
: 4
To prove Gauss' Theorem, we evaluate both
. ,
The answer should be the same.
V
S
S z
S z
S y
S x
S x y
div F dV
and F d S
=
=
=
=
+ =



115. 119
2
~ ~ ~ ~
~
2
~
~
1) We evaluate . Given 2 .
So,
( ) (2) ( )
1 2 .
Also, (1 2 ) .
The region is a part of the cylinder. So, we integrate by using
polar c
V
V V
div F dV F x i j z k
div F x z
x y z
z
div F dV z dV
= + +
  
= + +
  
= +
= +

 
oordinate of cylinder ,
; sin ;
where 0 2, 0 , 0 4.
2
x = cos y z z
dV d d dz
z
   
  

 
= =
=
     

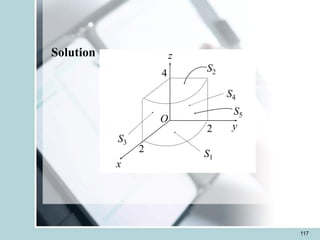
116. 120
 
2
2
2
2
2
2
2 4
0 0 0
2
2 4
0
0 0
2
0 0
2 2
0
0
0
0
~
Therefore,
(1 2 ) (1 2 )
[ ]
(20 )
[10 ]
(40)
40
20 .
20 .
V z
V
z dV z dzd d
z z d d
d d
d
d
div F dV






 
 
 


  
  
  
 




= = =
= =
= =
=
=
+ = +
= +
=
=
=
=
=
 =
   
 
 




117. 121
1
~ ~
~ ~
1
~ ~
~ ~ ~
~
~ ~ ~ ~
~
~ ~
2) Now, we evaluate . . .
i) : 0, ,
2 0
. ( 2 ).( ) 0
. 0.
S S
S
F d S F ndS
S z n k dS rdrd
F x i j k
F n x i j k
F ndS

=
= = - =
 = + +
 = + - =
 =
 


118. 122
2
2
2
~ ~
2
~ ~ ~ ~ ~
~ ~
~ ~ ~ ~ ~
~
2
2
0 0
~ ~
ii) : 4, ,
2 (4) 2 16
. ( 2 16 ).( ) 16.
Therefore for , 0 r 2, 0
2
. 16
16 .
S r
S z n k dS rdrd
F x i j k x i j k
F n x i j k k
S
F ndS rdrd







= =
= = =
 = + + = + +
 = + + =
   
 =
=
=
  

119. 123
3
3
~ ~
2
~ ~ ~
~
2
~ ~ ~ ~
~ ~
3
2 4
0 0
~ ~
iii) : 0, ,
2
. ( 2 ).( )
2.
Therefore for S , 0 2, 0 4
. ( 2)
16.
S x z
S y n j dS dxdz
F x i j z k
F n x i j z k j
x z
F ndS dzdx
= =
= = - =
 = + +
 = + + -
= -
   
 = -
=
= -
  

120. 124
4
4
~ ~
2 2
~ ~ ~ ~
~ ~
2
~ ~ ~ ~
~
~ ~
iv) : 0, ,
0 2 2
. (2 ).( ) 0.
. 0.
S
S x n i dS dydz
F i j z k j z k
F n j z k i
F ndS
= = - =
 = + + = +
 = + - =
 =


121. 125
2 2
5
5 5
~ ~
~
5 ~
~
5
~ ~
5
v) : 4,
2 2 4
2 2
4
1
( ).
2
By using polar coordinate of cylinder :
cos , sin ,
where for :
2, 0 , 0 4, 2
2
S x y dS d dz
S x i y j and S
x i y j
S
n
S
x i y j
x y z z
S
z dS d dz
 
   

  
+ = =
 = +  =
+

 = =

= +
= = =
=     =

122. 126
.
4
16
)
2
)(
sin
)(cos
2
(
.
).
sin
(cos
2
2.
kerana
;
sin
2
cos
2
)
sin
(
)
cos
(
2
1
2
1
2
1
2
1
).
2
(
.
5
2
0
4
0
2
~
~
2
2
2
2
~
~
~
2
~
~
~
~















+
=
=
+
=

+
=
=
+
=
+
=
+
=






+
+
+
=

  
= =

S z
dz
d
dS
n
F
y
x
j
y
i
x
k
z
j
i
x
n
F

123. 127
1 2 3 4 5
~ ~ ~ ~ ~ ~
~ ~ ~ ~ ~ ~
~ ~
Finally,
. . . . . .
0 16 16 0 16 4
20 .
. 20 .
Gauss' Theorem has been proved.
S S S S S S
S
F d S F d S F d S F d S F d S F d S
F d S
LHS RHS
 


= + + + +
= + - + + +
=
 =
=

     


124. 128
Stokes’ Theorem
If is a vector field on an open surface S and
boundary of surface S is a closed curve c,
therefore
  
=

S c
r
d
F
S
d
F
curl
~
~
~
~
~
F
~ ~
~
~ ~
x y z
i j k
curl F F
x y z
f f f
  
=   =
  

125. 129
Example
Surface S is the combination of
2 2
~ ~ ~
~
i) part of the cylinder 9 0
and 4 0.
ii) half of the circle with radius 3 at 4, and
iii) 0
, prove Stokes' Theorem
for this case.
a x y between z
z for y
a z
plane y
If F z i xy j xz k
+ = =
= 
=
=
= + +

126. 130
Solution
2 2
1
2
3
We can divide surface S as
S : x y 9 0 z 4 y 0
S : z 4, half of the circle with radius 3
S : y 0
for and
+ =   
=
=
z
y
x
3
4
O
S3
C2
S2
C1
S1
3

127. 131
We can also mark the pieces of curve C as
C1 : Perimeter of a half circle with radius 3.
C2 : Straight line from (-3,0,0) to (3,0,0).
Let say, we choose to evaluate first.
Given
~ ~
S
curl F d S


~
~
~
~
k
xz
j
xy
i
z
F +
+
=

128. 132
So,
~
~
~
~
~
~
~
~
~
)
1
(
)
(
)
(
)
(
)
(
)
(
)
(
k
y
j
z
k
z
y
xy
x
j
xz
x
z
z
i
xy
z
xz
y
xz
xy
z
z
y
x
k
j
i
F
curl
+
-
=










-


+








-


+










-


=






=

129. 133
By integrating each part of the surface,
2 2
1
1
~ ~
2 2
1
2 2
( ) : 9,
2 2
(2 ) (2 )
2 6
i For surface S x y
S x i y j
and S x y
x y
+ =
 = +
 = +
= + =

130. 134
)
(
3
1
6
2
2
~
~
~
~
1
1
~
j
y
i
x
j
y
i
x
S
S
n +
=
+
=


=
and
).
1
(
3
1
3
1
3
1
)
1
(
~
~
~
~
~
~
z
y
j
y
i
x
k
y
j
z
n
F
curl
-
=






+






 +
-
=

Then ,

131. 135
By using polar coordinate of cylinder ( because
is a part of the cylinder),
9
: 2
2
1 =
+ y
x
S
cos , sin ,
3, 0 0 4.
x y z z
dS d dz
where
dan z
   
 
  
= = =
=
=    

132. 136
Therefore,
  
~ ~
1
(1 )
3
1
sin 1
3
sin (1 ) ; 3
curl F n y z
z
z because
 
 
 = -
= -
= - =
Also, dz
d
dS 
3
=

133. 137
 
 
1 1
~ ~
~ ~
4
0 0
4
0
0
4
0
3 sin (1 )
3 (1 ) cos
3 (1 )(1 ( 1))
24
S S
z
curl F d S curl F n dS
z d dz
z dz
z dz



 

= =
  = 
= -
= - -
= - - -
= -
 
 



134. 138
(ii) For surface , normal vector unit to the
surface is
By using polar coordinate of plane ,
4
:
2 =
z
S
.
~
~
k
n =

 d
dr
r
dS
dan
z
r
y =
=
= 4
,
sin
0 r 3 and 0 .
where  
   

135. 139
 
2 2
~ ~ ~ ~
~
~ ~
~ ~
3
0 0
3
2
0 0
(1 )
sin
( sin )( )
sin
18
S S
r
r
curl F n z j y k k
y r
curl F d S curl F n dS
r rdrd
r d dr





 
 
= =
= =
 
  = - + 
 
 
= =
  = 
=
=
=
 
 
 

136. 140
(iii) For surface S3 : y = 0, normal vector unit
to the surface is
dS = dxdz
The integration limits :
.
~
~
j
n -
=
3 3 0 4
x and z
-    
So,
1
)
(
)
)
1
((
~
~
~
~
~
-
=
-

+
-
=

z
j
k
y
j
z
n
F
curl

137. 141
3 3
1 2 3
~ ~
~ ~
3 4
3 0
~ ~ ~ ~
~ ~ ~ ~
Then,
. .
( 1)
24.
. . . .
24 18 24
18.
S S
x z
S S S S
curl F d S curl F n dS
z dzdx
curl F d S curl F d S curl F d S curl F d S
=- =
=
= -
=
=
 = + +
= - + +
=
 
 
   

138. 142
~ ~
1
1
Now, we evaluate . for each pieces of the curve C.
i) is a half of the circle.
Therefore, integration for will be more easier if we use
polar coordinate for plane with radius
C
F d r
C
C

3, that is
3cos , 3sin dan z 0
where 0 .
r
x y
 
 
=
= = =
 

139. 143
~ ~ ~
~
~
~
~ ~
~
~ ~
(3cos )(3sin )
9sin cos
and
3sin 3cos .
F z i xy j xzk
j
j
dr dx i dy j dzk
d i d j
 
 
   
 = + +
=
=
= + +
= - +

140. 144
1
2
~ ~
2
0
~ ~
3
0
From here,
. 27sin cos .
. 27sin cos
9cos
18.
C
F d r d
F d r d


  
  

=
 =
 
= -
 
=
 

141. 145
2
2
~ ~ ~
~
~
~ ~
ii) Curve is a straight line defined as
, 0 z 0, where 3 3.
Therefore,
0.
. 0.
C
C
x t y and t
F z i xy j xz k
F d r
= = = -  
= + +
=
 =


142. 146
1 2
~ ~ ~ ~ ~ ~
~ ~ ~
~
. . .
18 0
18.
We already show that
. .
Stokes' Theorem has been proved.
C C C
S C
F d r F d r F d r
curl F d S F d r
 = +
= +
=
=

  
 