1. The document discusses using the Echelon method to solve systems of linear equations.
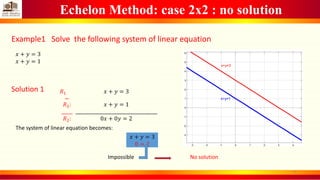
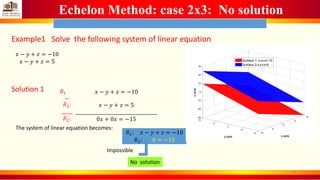
2. Examples are provided to demonstrate solving systems with 2x2 and 2x3 equations that have no solution, one solution, or an infinite number of solutions (represented by a line or surface).
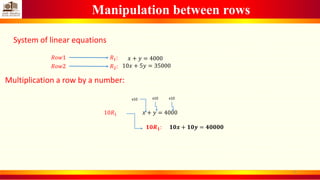
3. Manipulations between rows are explained, such as multiplying a row by a constant or adding rows together.