Документ представляет собой введение в машинное обучение, описывающее основные его понятия, задачи и методы. Рассматриваются типы обучения, включая обучении с учителем и без учителя, а также примеры практических задач, таких как распознавание символов и предсказание цен. Также обсуждаются различные виды признаков и описания объектов, используемых в моделях машинного обучения.







































![Литература
[1] Hastie T., Tibshirani R., Friedman J. The elements of statistical learning. Springer,
2001.
[2] Ripley B.D. Pattern recognition and neural networks. Cambridge University Press,
1996.
[3] Bishop C.M. Pattern recognition and machine learning. Springer, 2006.
[4] Duda R. O., Hart P. E., Stork D. G. Pattern classification. New York: JohnWiley
and Sons, 2001.
[5] Mitchell T. Machine learning. McGraw Hill,1997.
[6] Воронцов К.В. Математические методы обучения по прецедентам. Курс
лекций. Москва, ВЦ РАН, 2005. ØØÔ »»ÛÛÛº ׺ÖÙ»ÚÓÖÓÒ»Ø Ò º ØÑÐ](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-45-320.jpg)
![[7] Загоруйко Н.Г. Прикладные методы анализа данных и знаний. Новосибирск:
Изд-во Ин-та математики, 1999.
[8] Николенко С. Машинное обучение. Курс лекций. СПб.: ПОМИ РАН, 2006.
ØØÔ »»ÐÓ ºÔ Ñ ºÖ ׺ÖÙ» × Ö Ý»](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-46-320.jpg)
![[9] Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: основы
моделирования и первичная обработка данных. М.: Финансы и статистика,
1983.
[10] Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика:
исследование зависимостей. М.: Финансы и статистика, 1985.
[11] Айвазян С.А., Бухштабер В.М., Енюков И.С., Мешалкин Л.Д. Прикладная
статистика: классификация и снижение размерности. М.: Финансы и
статистика, 1989.
[12] Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. М.: Наука,
1974.
[13] Вапник В.Н. Восстановление зависимостей по эмпирическим данным. М.:
Наука, 1979.
[14] Vapnik V.N. The nature of statistical learning theory. New York: Springer, 1995.
[15] Vapnik V.N. Statistical learning theory. New York: John Wiley, 1998.
wiki-портал: ØØÔ »»ÛÛÛºÑ Ò Ð ÖÒ Ò ºÖÙ](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-47-320.jpg)













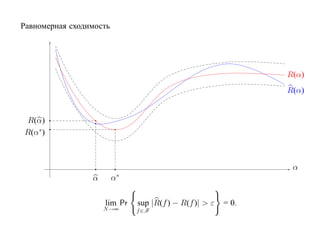
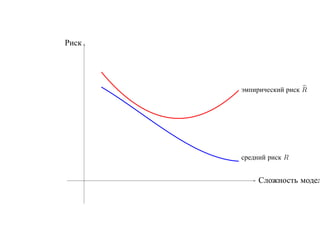
![Пусть F = {f : f (x, α), α ∈ [0, 1]} — класс решающих правил
R(α) — средний риск, R(α) — эмпирический риск на функции f (x, α)
R(α) R(α)
∗
R(α)
R(α )
α
α∗ α
R(α) далеко от минимального значения R(α∗ ).
lim Pr |R(f ) − R(f )| > ε = 0.
N →∞](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-61-320.jpg)




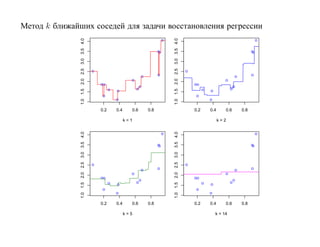






![1.8.5. Метод стохастической минимизации
[Robins, Monroe, 1951, Айзерман, Браверман, Розоноэр, 1965, Amari, 1967,
Цыпкин, 1971, 1973].
Пусть класс F решающих функций параметризован вектором α:
F = {f (x) = f (x, α) : α ∈ Rq } .
Требуется найти α∗, минимизирующее функционал
R(α) = L f (x, α)| y dP (x, y).
X×Y
Метод основан на итерациях
α(k+1) = α(k) − γk · ∇αL f (x(k), α(k))|y (k) (k = 1, 2, . . . , N ).
При некоторых необременительных ограничениях на γk и ∇α L f (x, α)| y процесс
сходится к α∗, минимизирующему R(α).
Для гарантированной корректной работы выборка должна быть очень большой.
Далее этот метод в курсе не рассматривается.](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-75-320.jpg)




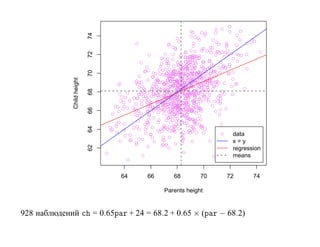
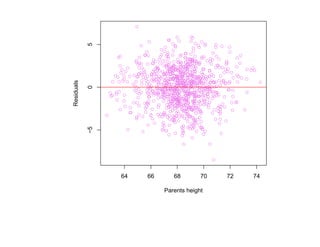
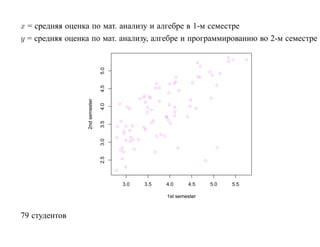
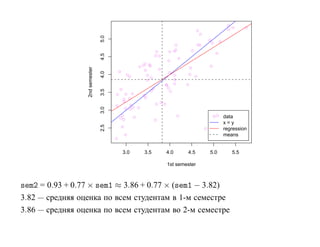
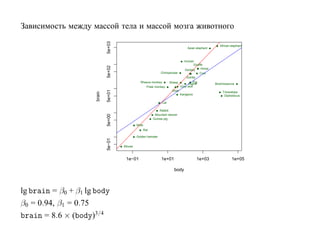








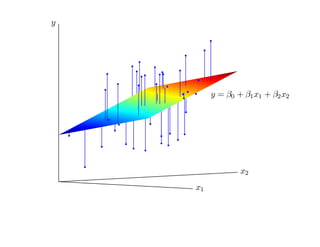
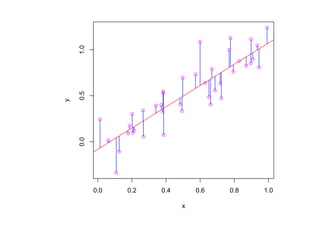
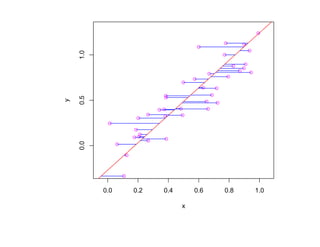
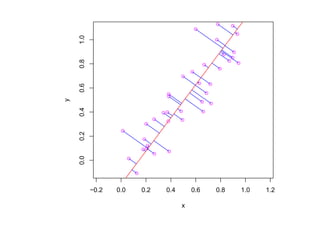
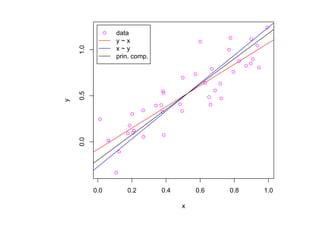



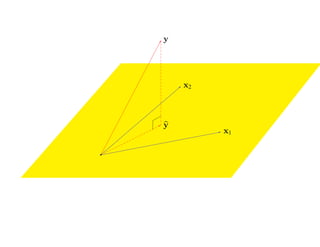















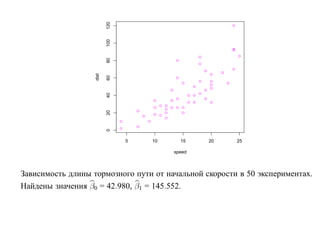
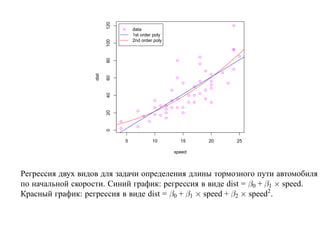




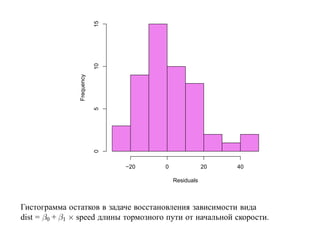

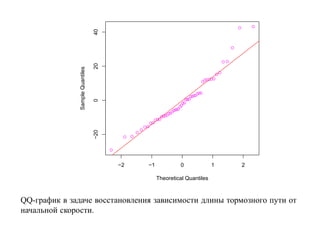

![корреляции остатков. Если D L(α) < D < D U(α) или 4 − D U(α) < D < 4 − D L(α),
то критерий не позволяет принять решение о наличии или отсутствии корреляции
остатков. Если D U(α) < D < 4 − D U(α), то гипотеза о наличии корреляции
остатков отклоняется. Таблицы критических значений D L(α) и D U(α) для
различных α, N , p приведены, например, в [Дрейпер, Смит Т. 1, С. 211].](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-127-320.jpg)


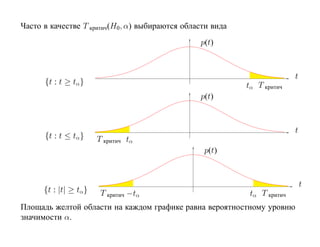
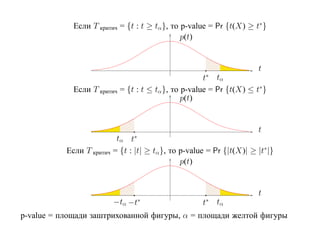
![2.1.2. p-value
p-value принадлежит интервалу [0, 1] и вычисляется по выборочному значению t∗
статистики t(X) (и зависит также от критерия и гипотезы H0, но не зависит от α).
p-value — это минимальное значение уровня значимости α, при котором данное
значение t∗ статистики t(X) принадлежит критической области T критич(H0, α):
p-value(t∗ , H0) = inf {α : t∗ ∈ T критич(H0, α)}
Из этого определение вытекает следующее основное свойство p-value.
Если p-value меньше α, то гипотеза H0 отвергается.
Иначе гипотезу H0 отвергнуть нельзя.](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-131-320.jpg)


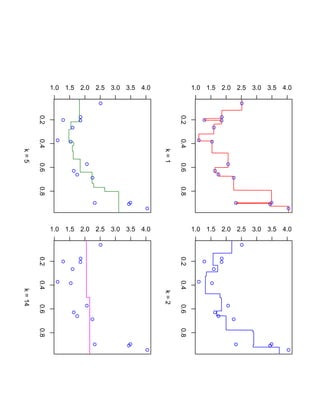
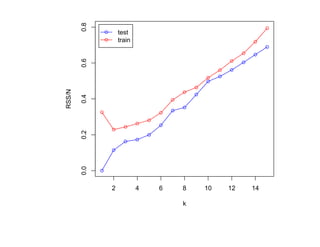
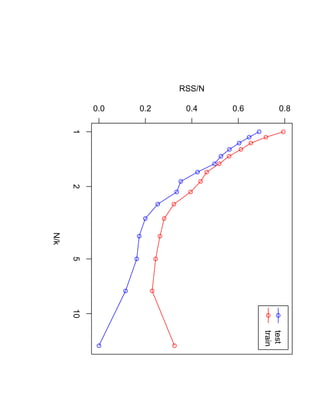





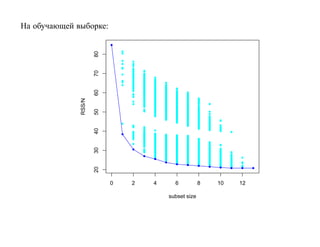
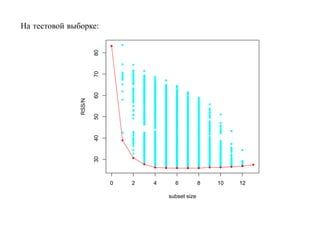
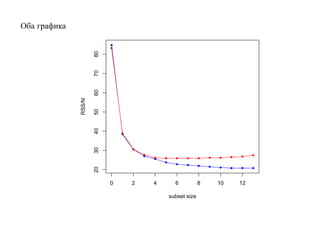


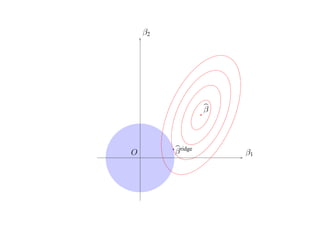








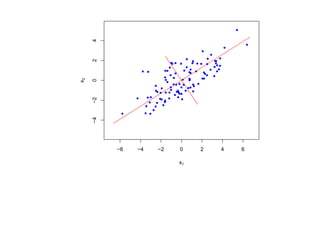

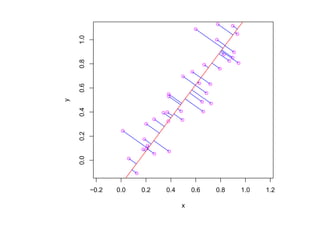

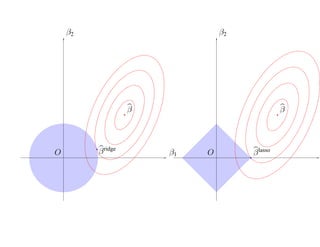
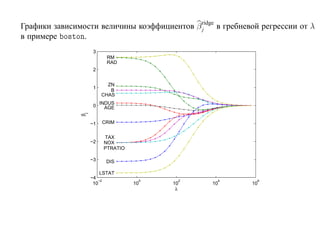

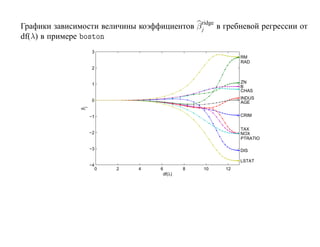

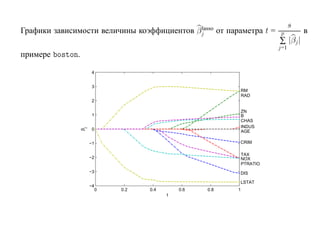


















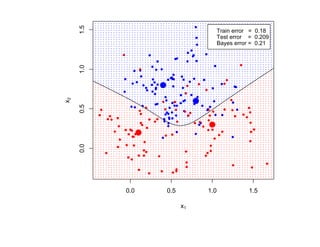



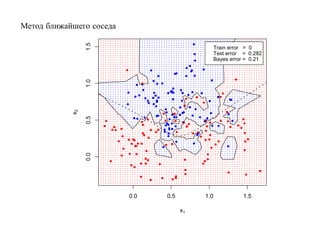
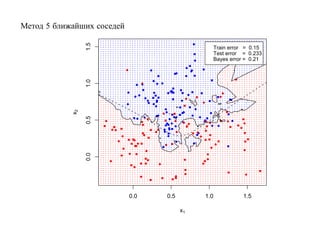
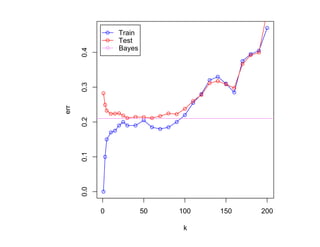










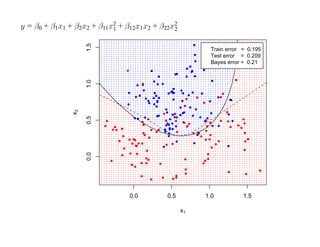

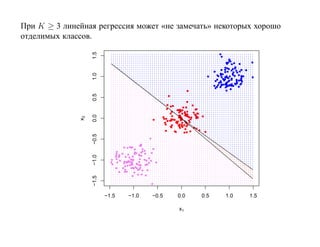



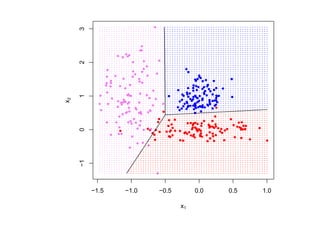



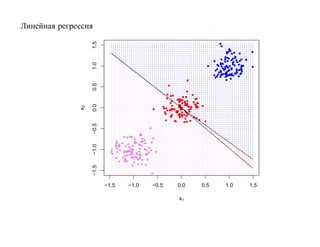
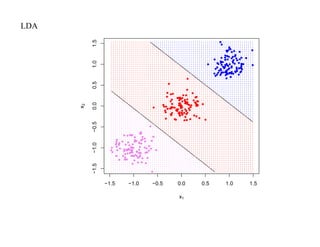
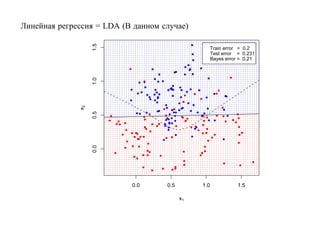

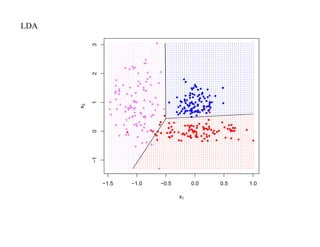
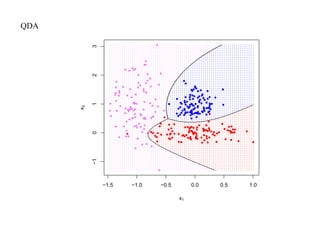
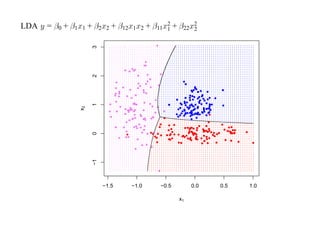





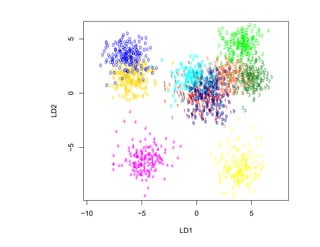









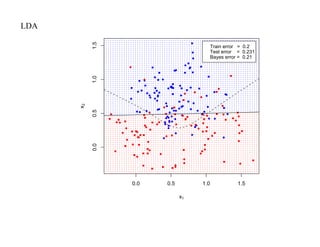
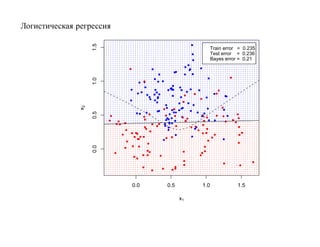
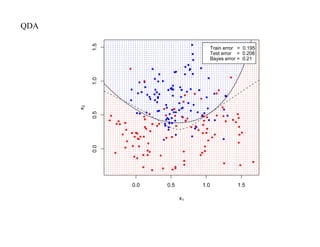










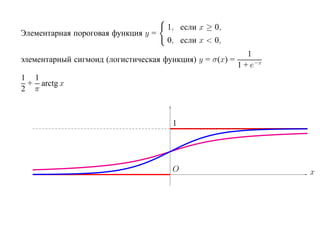

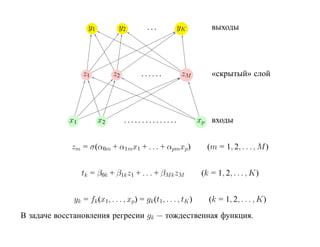




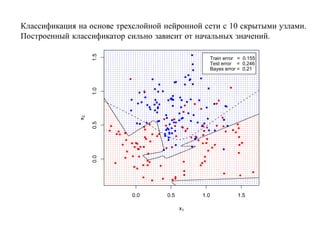

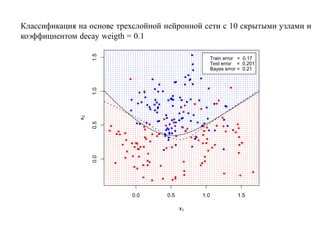
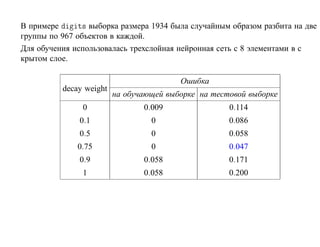


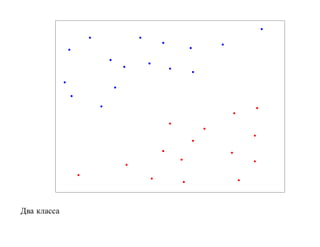
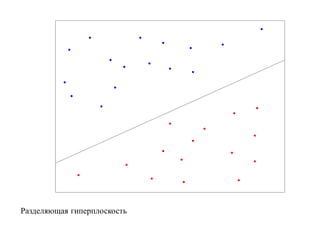
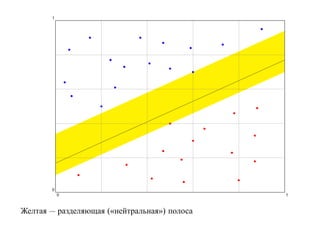

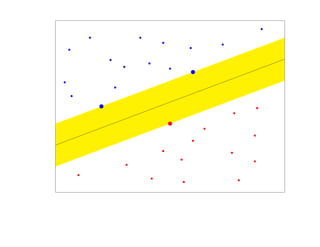



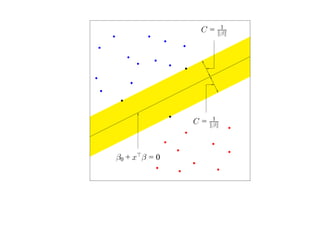



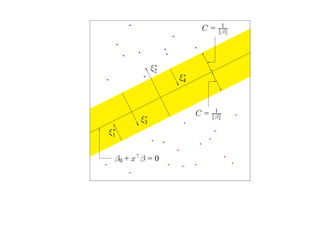




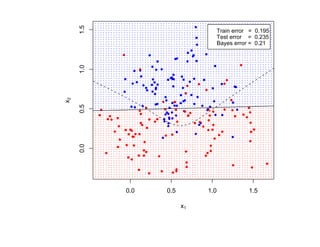







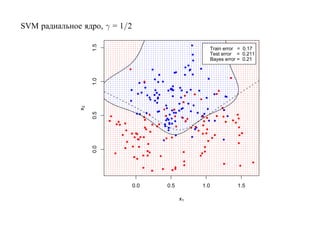
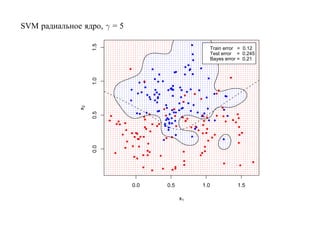
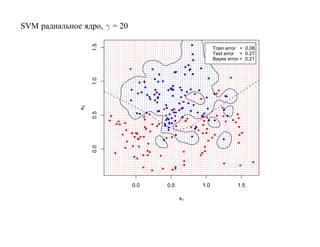
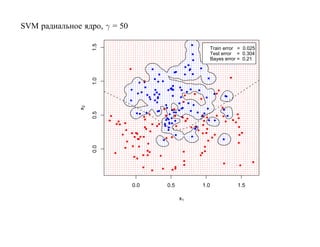
![SVM может быть рассмотрен как метод штрафов.
Можно показать, что наша задача сводится к задаче оптимизации
N
min ∑ 1 − yi h(xi) β + β0 + α β 2,
β, β0 +
i=1
где [·]+ означает положительную часть.
Целевая функция имеет вид «потери + штраф».](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-293-320.jpg)
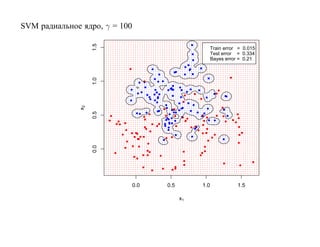
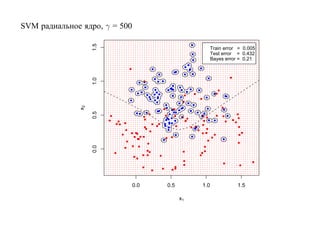
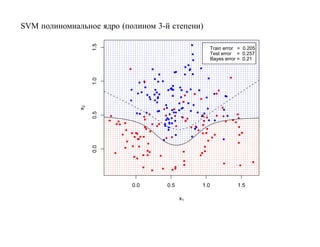


























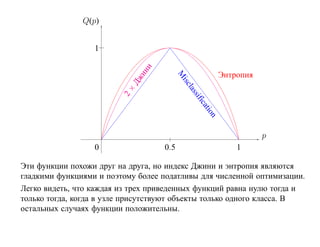































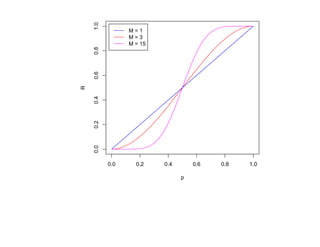

![6.2. Бустинг
[R.E. Schapire, 1990]
Идея: если уж так сложно добиться независимости экспертов, давайте попробуем
строить последовательность классификаторов, каждый из которых осведомлен об
ошибках предыдущих.
Пусть для простоты только два класса {−1, 1}.](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-369-320.jpg)

![6.2.2. AdaBoost
(от Adaptive Boosting) [Freund, Schapire, 1995]
Будем использовать веса w1, w2, . . . , wN .
На первой итерации wi = 1/N (i = 1, 2, . . . , N ) и алгоритм построения f1 работает
в обычном режиме.
На m-й итерации увеличиваются веса тех прецедентов, на которых на (m − 1)-й
итерации была допущена ошибка, и уменьшаются веса тех прецедентов, которые
на предыдущей итерации были классифицированы правильно.](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-371-320.jpg)





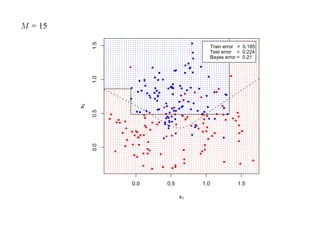
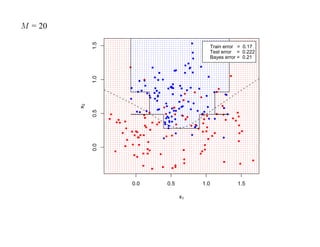
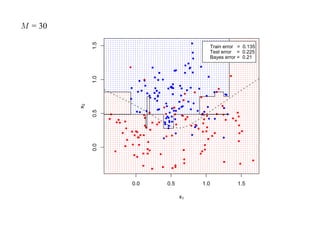
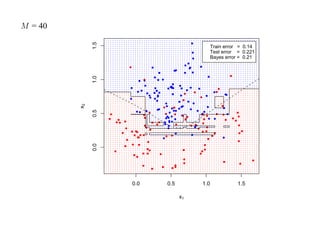
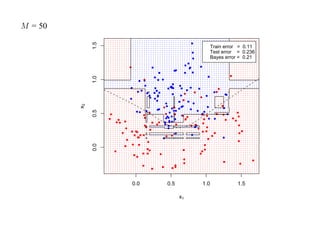
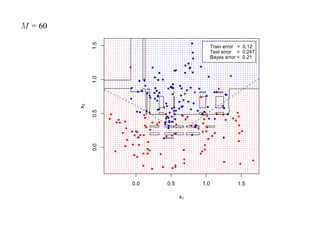
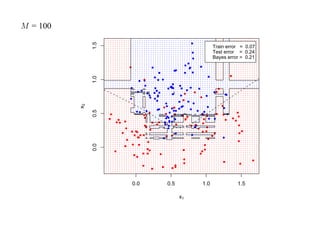
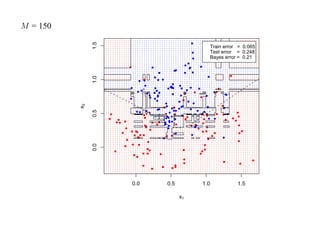
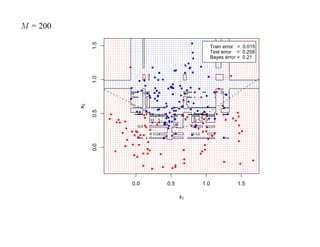
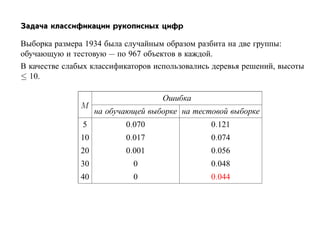


















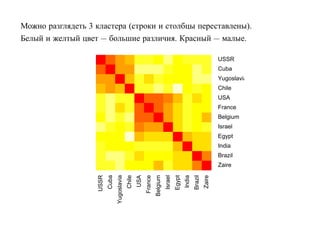




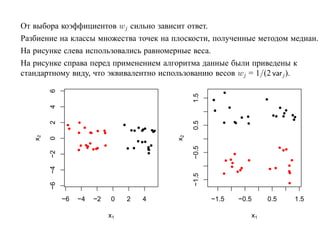











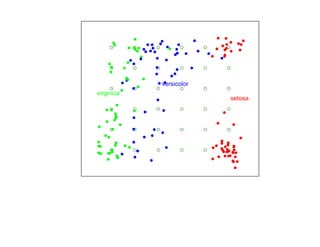
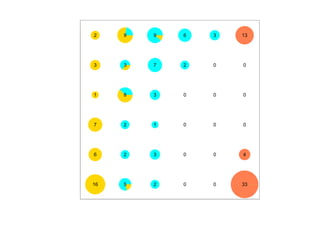






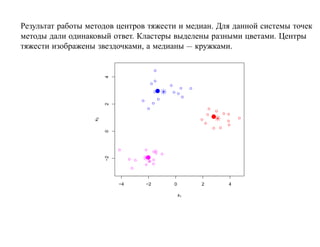
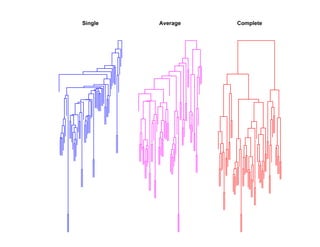
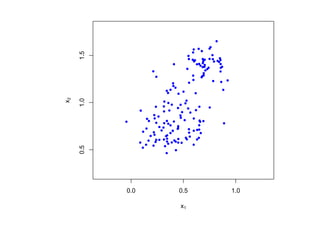
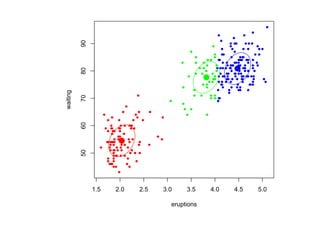
![7.3.4. Метод нечетких множеств
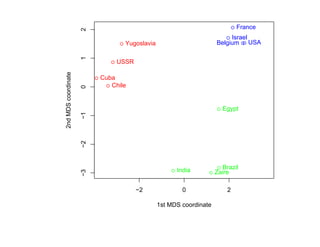
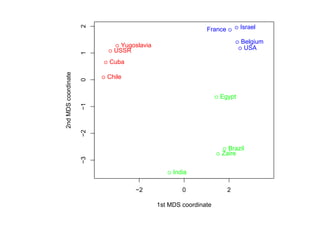
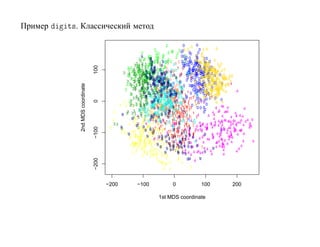
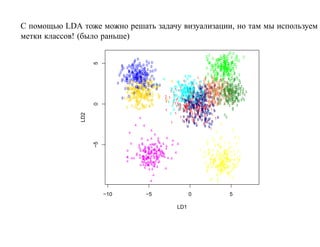
Рассмотрим подход к задаче кластеризации, навеянный нечеткой логикой.
Зафиксируем некоторое натуральное K и рассмотрим множество
U = {1, 2, . . . , K}, которое назовем универсом.
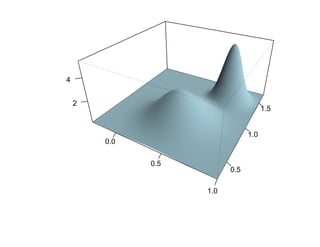
Нечетким множеством называется отображение V : U → [0, 1], для которого
0 ≤ V (i) ≤ 1, (i = 1, 2, . . . , N ).
Отображение V называется также функцией принадлежности, а значение V (i) —
степенью принадлежности элемента i нечеткому множеству V .
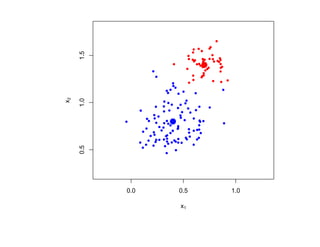
Предположим, что кластеры являются нечеткими множествами.
Пусть тогда uik есть степень принадлежности i-го объекта k-му кластеру.
Имеем
K
∑ uik = 1, 0 ≤ uik ≤ 1, (i = 1, 2, . . . , N, k = 1, 2, . . . , K).
k=1](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-438-320.jpg)





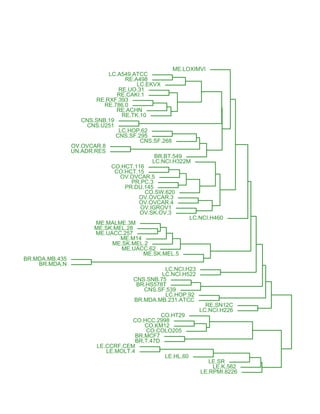










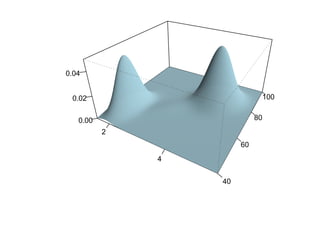
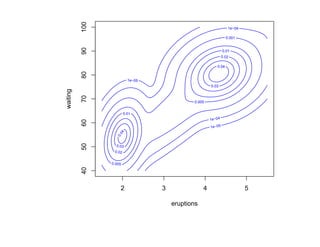


![Глава 8
Теория машинного обучения
Истоки: В.П. Вапник, А.Я. Червоненкис [1971]](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-475-320.jpg)







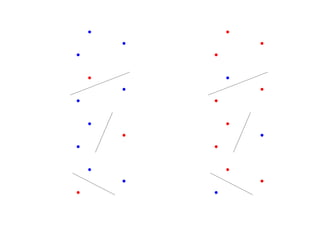



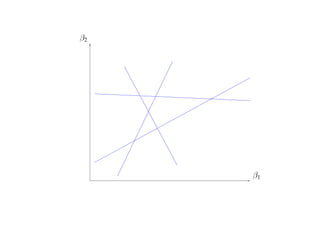





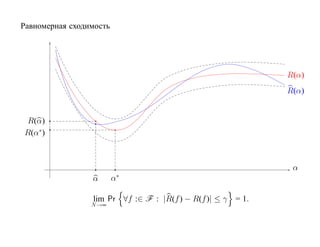
![Пусть F = {f : f (x, α), α ∈ [0, 1]} — класс решающих правил
R(α) — средний риск, R(α) — эмпирический риск на функции f (x, α)
R(α) R(α)
∗
R(α)
R(α )
α
α∗ α
R(α) далеко от минимального значения R(α∗ ).
lim Pr |R(f ) − R(f )| ≤ γ = 1.
N →∞](https://image.slidesharecdn.com/mlpres-100905115539-phpapp02/85/Machine-Learning-494-320.jpg)