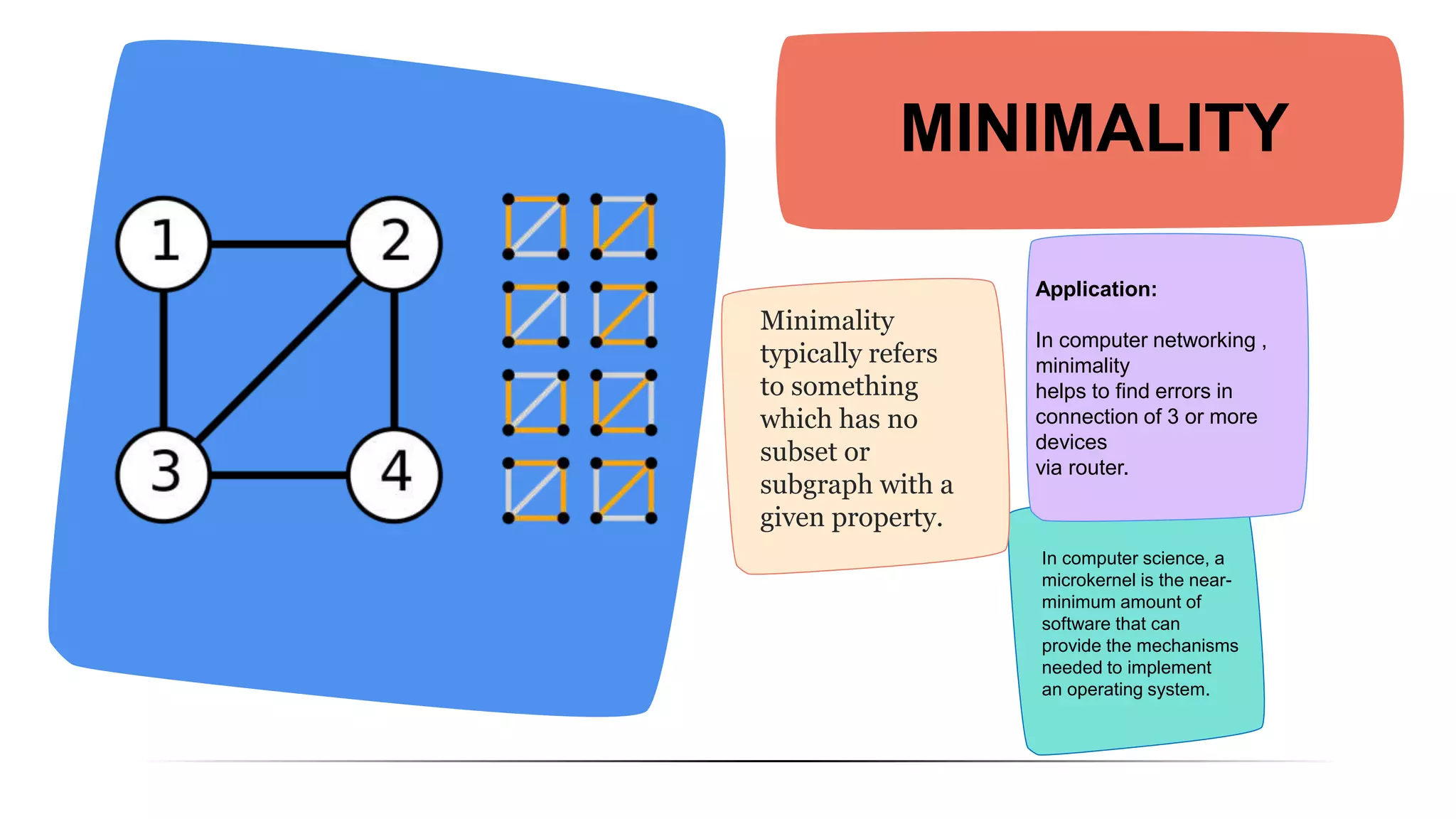
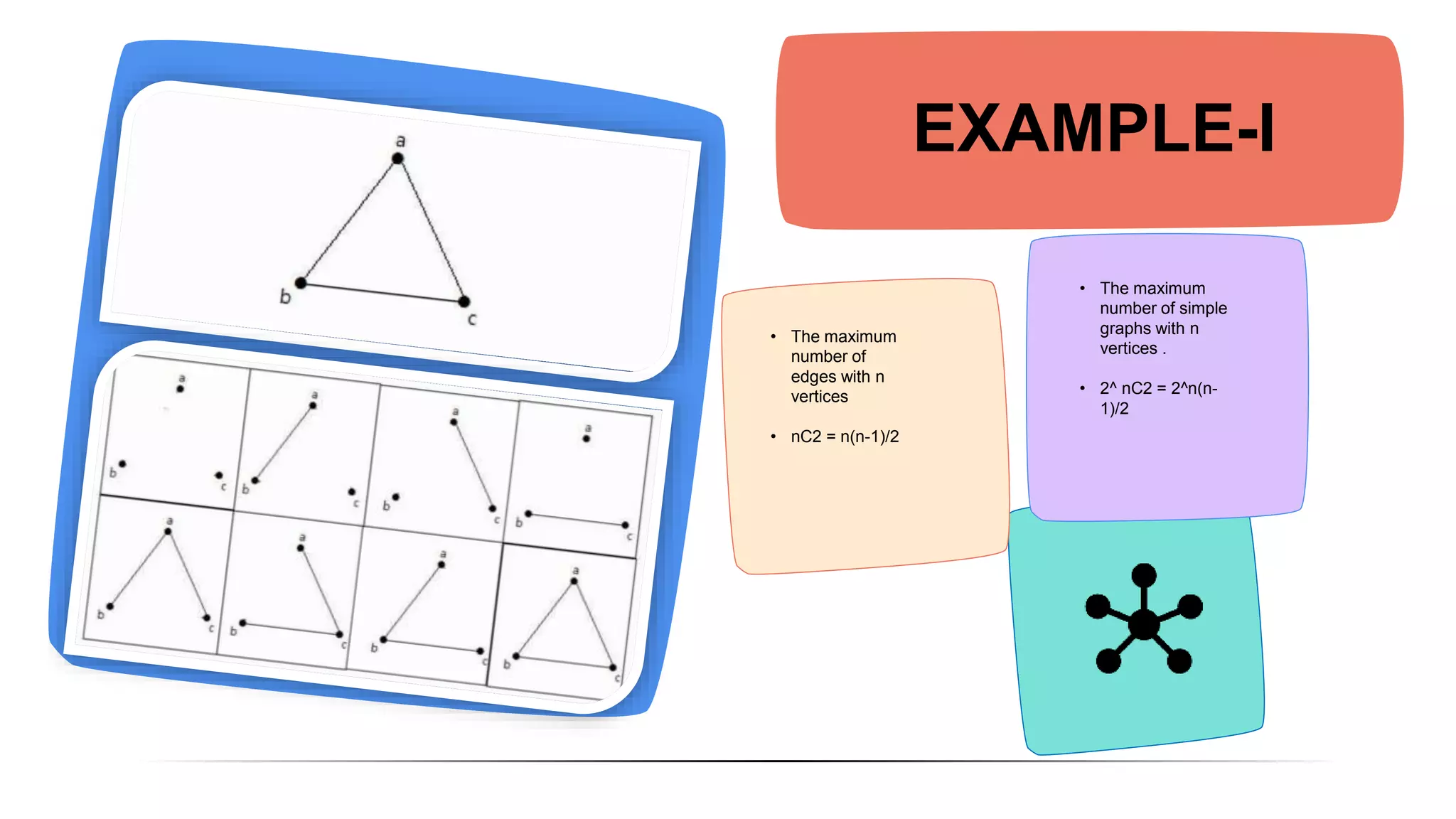
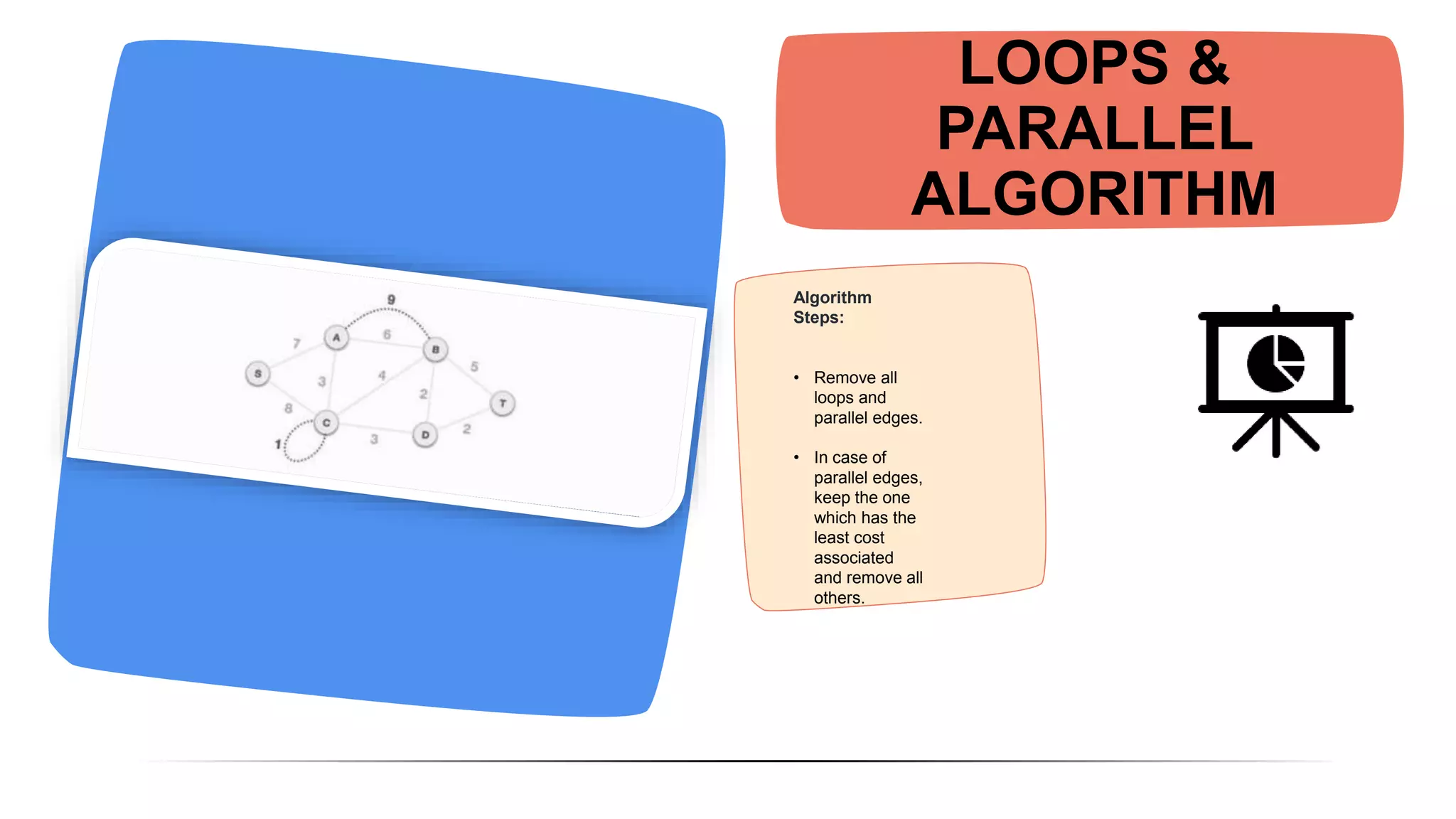
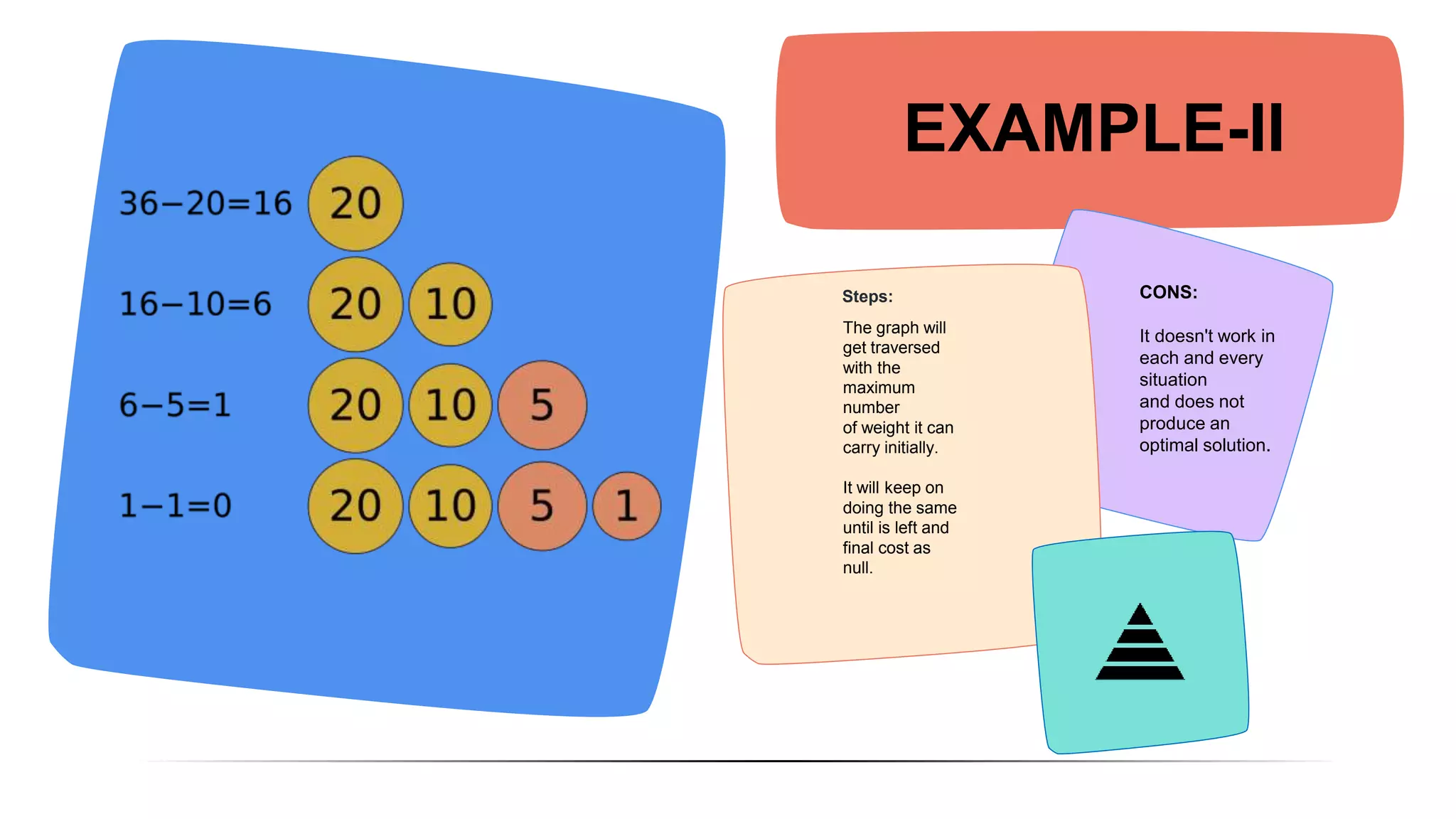
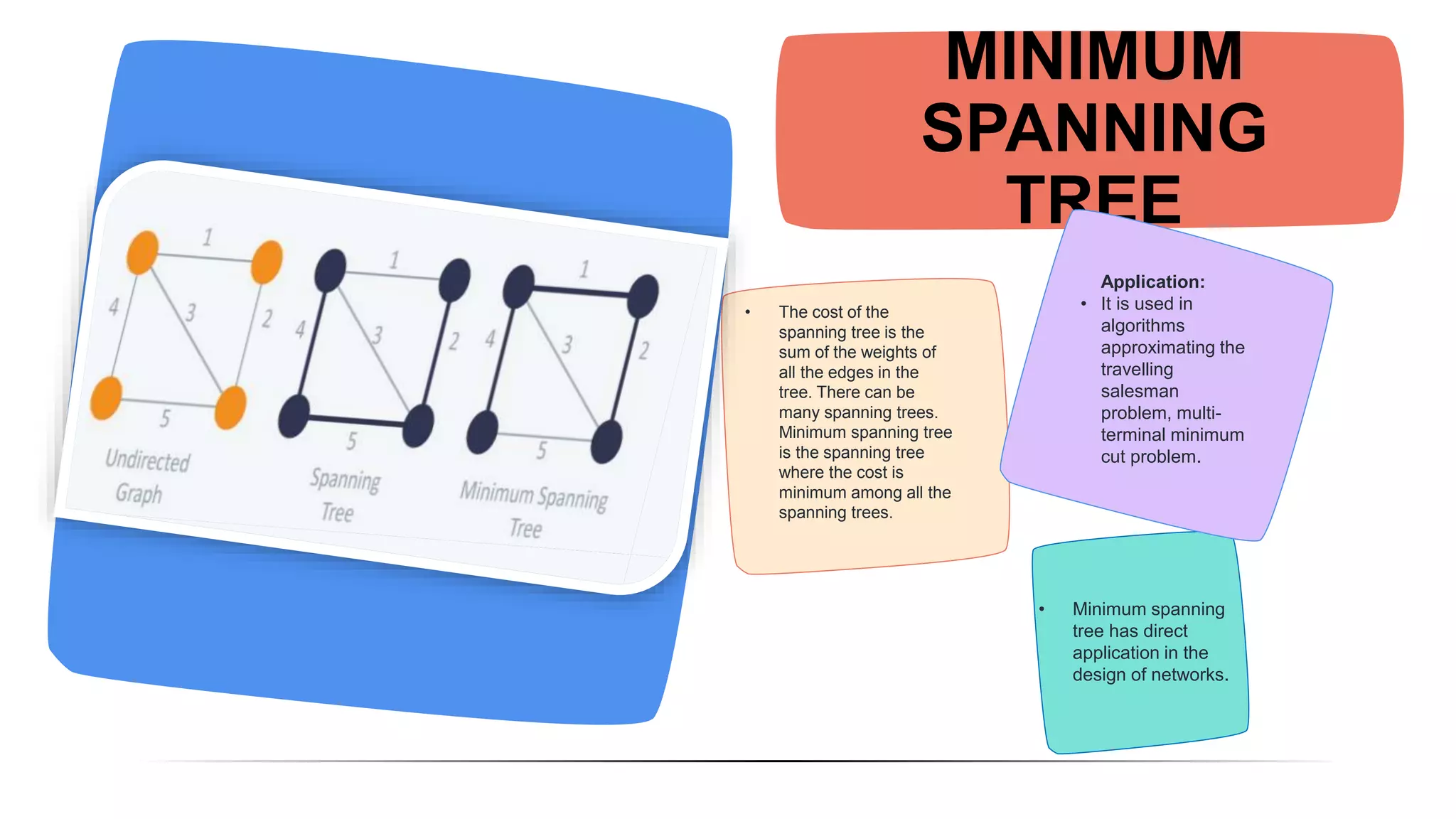
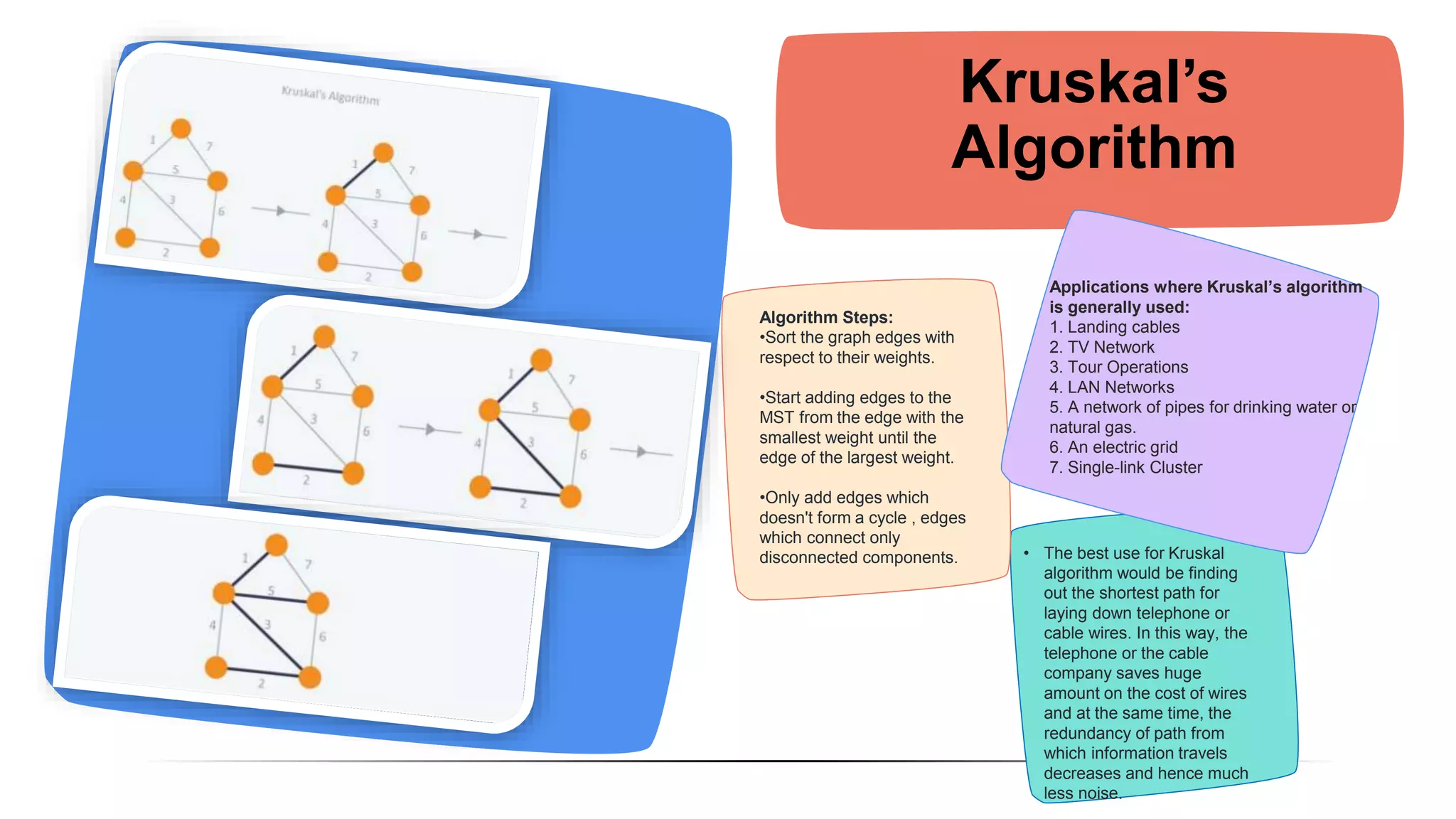
The document discusses and compares Kruskal's algorithm and Prim's algorithm for finding minimum spanning trees in graphs. Both algorithms build up a minimum spanning tree by adding edges to the tree one by one. Kruskal's algorithm sorts edges by weight and adds the smallest weight edge that does not create a cycle. Prim's algorithm maintains two vertex sets and adds the cheapest edge between them. The performance of the algorithms depends on factors like number of vertices, with Prim's running faster on large graphs and Kruskal's faster on small graphs.

1. EM-IV
PRESENTATION

2. APPLICATI
ON IN
REAL LIFE
:
Kruskal’s Algorithm
&
& &
Prim’s Algorithm
16/03/2021 EM-IV PRESENTATION 2

3. COST OF
GRAPH
MINIMALITY LOOPS &
PARALLEL
ALGORITHM
GREEDY
ALGORITHM
MINIMUM
SPANNING
TREE
KRUSKAL’S
& PRIM’S
ALGORITHM
AGENDA

4. MINIMALITY
Application:
In computer networking ,
minimality
helps to find errors in
connection of 3 or more
devices
via router.
Minimality
typically refers
to something
which has no
subset or
subgraph with a
given property.
In computer science, a
microkernel is the near-
minimum amount of
software that can
provide the mechanisms
needed to implement
an operating system.

5. EXAMPLE-I
• The maximum
number of
edges with n
vertices
• nC2 = n(n-1)/2
• The maximum
number of simple
graphs with n
vertices .
• 2^ nC2 = 2^n(n-
1)/2

6. LOOPS &
PARALLEL
ALGORITHM
Algorithm
Steps:
• Remove all
loops and
parallel edges.
• In case of
parallel edges,
keep the one
which has the
least cost
associated
and remove all
others.

7. GREEDY
ALGORITHM
Algorithm Steps: Application:
• Greedy algorithms
allow to find a
globally optimal
solution for a given
problem by making
successive locally
optimal choices.
• We can model different
communications networks
using vertices to represent
devices and edges to
represent the particular
type of communications
links of interest.
• A candidate set, from which a
solution is created
• A selection function, which chooses
the best candidate to be added to
the solution
• A feasibility function, that is used to
determine if a candidate can be
used to contribute to a solution
• An objective function, which assigns
a value to a solution, or a partial
solution, and
• A solution function, which will
indicate when we have discovered a
complete solution
• Greedy algorithms are
often used in ad hoc
mobile networking to
efficiently route
packets with the fewest
number of hops and
the shortest delay
possible.

8. EXAMPLE-II
• We can model different
communications networks
using vertices to represent
devices and edges to
represent the particular
type of communications
links of interest.
The graph will
get traversed
with the
maximum
number
of weight it can
carry initially.
It will keep on
doing the same
until is left and
final cost as
null.
Steps: CONS:
It doesn't work in
each and every
situation
and does not
produce an
optimal solution.

9. COST OF
GRAPH
• Given a directed graph,
which may contain cycles,
where every edge has
weight, the task is to find
the minimum cost of any
simple path from a given
source vertex ‘s’ to a given
destination vertex ‘t’.
:Depending upon the total
cost and number of
edges present , via multiple
routes ,
average cost describes the
complexity of
a graph/tree .

10. MINIMUM
SPANNING
TREE
• The cost of the
spanning tree is the
sum of the weights of
all the edges in the
tree. There can be
many spanning trees.
Minimum spanning tree
is the spanning tree
where the cost is
minimum among all the
spanning trees.
• Minimum spanning
tree has direct
application in the
design of networks.
Application:
• It is used in
algorithms
approximating the
travelling
salesman
problem, multi-
terminal minimum
cut problem.

11. Kruskal’s
Algorithm
Algorithm Steps:
•Sort the graph edges with
respect to their weights.
•Start adding edges to the
MST from the edge with the
smallest weight until the
edge of the largest weight.
•Only add edges which
doesn't form a cycle , edges
which connect only
disconnected components.
Applications where Kruskal’s algorithm
is generally used:
1. Landing cables
2. TV Network
3. Tour Operations
4. LAN Networks
5. A network of pipes for drinking water or
natural gas.
6. An electric grid
7. Single-link Cluster
• The best use for Kruskal
algorithm would be finding
out the shortest path for
laying down telephone or
cable wires. In this way, the
telephone or the cable
company saves huge
amount on the cost of wires
and at the same time, the
redundancy of path from
which information travels
decreases and hence much
less noise.

12. Prim’s Algorithm
Algorithm Steps:
•Maintain two disjoint sets of
vertices. One containing vertices
that are in the growing spanning
tree and other that are not in the
growing spanning tree.
•Select the cheapest vertex that
is connected to the growing
spanning tree and is not in the
growing spanning tree and add
it into the growing spanning tree.
This can be done using Priority
Queues. Insert the vertices, that
are connected to growing
spanning tree, into the Priority
Queue.
•Check for cycles. To do that,
mark the nodes which have
been already selected and insert
only those nodes in the Priority
Queue that are not marked.
Applications where Prim’s
algorithm is generally used:
1.All the applications stated in
the Kruskal’s algorithm’s
applications can be resolved
using Prim’s algorithm (use in
case of a dense graph).
2. Network for roads and Rail
tracks connecting all the
cities.
3. Irrigation channels and
placing microwave towers
4. Designing a fiber-optic grid
or ICs.
5. Travelling Salesman
Problem.
6. Cluster analysis.
7. Pathfinding algorithms
used in AI(Artificial
Intelligence).
8. Game Development

13. 16/03/2021 EM-IV PRESENTATION 13
The performance of the two algorithms could differ
depending upon the certain factors such as the number of
vertices. Prim’s algorithm runs in O(V2) time and works
well in the massive graphs while Kruskal’s algorithm
consumes O(log V) and perform suitably with small
graphs. Although, among both of the algorithm Kruskal’s
algorithm can generate better results.

14. 16/03/2021 EM-IV PRESENTATION 14
"Texas Birth Index, Nolan County, 1903-1997".
Obituary (February 22, 2009). "Alice (Hutter) Prim In Memoriam". Austin
American-Statesmen. Retrieved May 3, 2013.
Leland Johnson (1997). "A History of Exceptional Service in the National
Interest" (PDF). Retrieved July 20, 2016.
Cormen, Thomas; Charles E Leiserson, Ronald L Rivest, Clifford Stein
(2009). Introduction To Algorithms (Third ed.). MIT Press. pp. 631. ISBN 978-
0262258104.
Kruskal, J. B. (1956). "On the shortest spanning subtree of a graph and the traveling
salesman problem". Proceedings of the American Mathematical Society. 7 (1): 48–
50. doi:10.1090/S0002-9939-1956-0078686-7. JSTOR 2033241.
Quinn, Michael J.; Deo, Narsingh (1984). "Parallel graph algorithms". ACM Computing
Surveys. 16 (3): 319–348. doi:10.1145/2514.2515.
Grama, Ananth; Gupta, Anshul; Karypis, George; Kumar, Vipin (2003). Introduction to
Parallel Computing. pp. 412–413. ISBN 978-0201648652.
Jump up to:a b Osipov, Vitaly; Sanders, Peter; Singler, Johannes (2009). "The filter-
kruskal minimum spanning tree algorithm" (PDF). Proceedings of the Eleventh
Workshop on Algorithm Engineering and Experiments (ALENEX). Society for Industrial
and Applied Mathematics: 52–61.
Katsigiannis, Anastasios; Anastopoulos, Nikos; Konstantinos, Nikas; Koziris, Nectarios
(2012). "An approach to parallelize kruskal's algorithm using helper
threads" (PDF). Parallel and Distributed Processing Symposium Workshops & PHD
Forum (IPDPSW), 2012 IEEE 26th International: 1601–1610.

15. Thank you
16/03/2021 EM-IV PRESENTATION 15