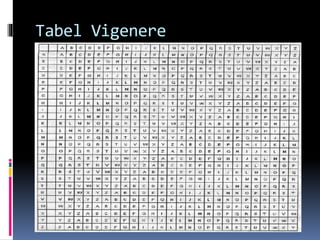
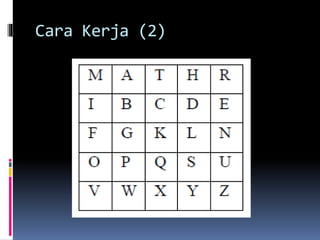
Dokumen tersebut membahas tentang kriptografi secara singkat dalam 3 kalimat. Pertama, kriptografi adalah ilmu dan teknik untuk menjaga kerahasiaan data digital dengan mengenkripsinya. Kedua, terdapat beberapa algoritma kriptografi seperti simetris dan asimetris. Ketiga, sejarah kriptografi dimulai sejak zaman Mesir Kuno hingga Perang Dunia II.

1. wilfridus.bambang@eng.maranatha.edu
KRIPTOGRAFI

2. Data Digital
 Gambar
 Audio
• teks
sekuritaskomputer
• Video

3. Konsep
 mekanisme untuk menjaga kerahasiaan data,
 melakukan perubahan kode (chiper) sehingga
menjadi tidak dapat terbaca secara langsung.
 Sistem pengkodean menggunakan kamus
data yang telah didefinisikan
 melakukan penggantian karakter dari suatu
informasi,

4. Tujuan
 melindungi informasi agar tidak terlihat oleh
pihak yang tidak diotorisasi,
 nomor kartu kredit,
 password suatu aplikasi,
 data-data yang terdapat di komputer, dll
 Mengurangi resiko kerugian besar terhadap
aspek kerahasiaan data
 pengguna yang tidak berhak dapat melakukan
pengaksesan informasi yang penting,

5. Skema

6. Terminologi
 Enkripsi (encryption): proses menyandikan
plainteks menjadi cipherteks.
 Dekripsi (decryption): Proses
mengembalikan cipherteks menjadi
plainteks semula.

7. Notasi Matematika
Misalkan:
C = chiperteks
P = plainteks
 Fungsi enkripsi E memetakan P ke C,
E(P) = C
 Fungsi dekripsi D memetakan C ke P,
D(C) = P
Fungsi enkripsi dan dekripsi harus memenuhi sifat:
D(E(P)) = P

8. Sejarah

9. Asal Kata
 Kriptografi (cryptography)
 Kata cryptography berasal dari bahasa
Yunani: krupto (hidden atau secret) dan
grafh (writing)
Artinya “secret writing”

10. Definisi
 Definisi lama:
ilmu dan seni untuk menjaga kerahasian pesan
dengan cara menyandikannya ke dalam bentuk
yang tidak dapat dimengerti lagi maknanya.
 Definisi baru:
ilmu dan seni untuk menjaga keamanan
pesan (message) [Schneier, 1996].
“art and science to keep message secure”

11. Kriptografi dalam Peradaban
 Tercatat Bangsa Mesir 4000 tahun yang
lalu menggunakan hieroglyph yang tidak
standard untuk menulis pesan

12. Kriptografi dalam Peradaban (2)
 Di Yunani, kriptografi sudah digunakan 400
BC
 Alat yang digunakan: scytale

13. Kriptografi dalam Peradaban (3)
 Tidak ditemukan catatan kriptografi di
Cina dan Jepang hingga abad 15.
 Pada Abad ke-17, sejarah
kriptografi pernah mencatat
korban di Inggris.
 Queen Mary of Scotland,
dipancung setelah pesan
rahasianya dari balik penjara
(pesan terenkripsi yang isinya
rencana membunuh Ratu
Elizabeth I) pada Abad
Pertengahan berhasil
dipecahkan oleh Thomas
Phelippes, seorang pemecah
kode

14. Cipher yang digunakan Queen Mary of
Scotland

15. Kriptografi dalam WW II
 Perang Dunia ke II,
Pemerintah Nazi Jerman
membuat mesin enkripsi
yang dinamakan Enigma.
 Enigma cipher berhasil
dipecahkan oleh pihak
Sekutu, dan dikatakan
sebagai faktor yang
memperpendek perang
dunia ke-2

16. Kriptografi dalam Peradaban (4)
 Sejarah lengkap kriptografi dapat ditemukan
di dalam buku David Kahn, “The
Codebreakers”
 Empat kelompok orang yang menggunakan
dan berkontribusi pada kriptografi:
1. Militer (termasuk intelijen dan mata-mata)
2. Korp diplomatik
3. Diarist
4. Lovers

17. Layanan Kriptografi

18. 1. Confidentiality
 Layanan yang digunakan untuk menjaga
isi pesan dari siapapun yang tidak berhak
untuk membacanya.

19. 2. Integrity
Layanan yang menjamin
bahwa pesan masih
asli/utuh atau belum
pernah dimanipulasi
selama pengiriman.
“Apakah pesan yang
diterima masih asli atau
tidak mengalami
perubahan
(modifikasi)?”.

20. 3. Authentication
Layanan yang untuk
mengidentifikasi kebenaran
pihak-pihak yang
berkomunikasi (user
authentication) dan untuk
mengidentifikasi kebenaran
sumber pesan (data origin
authentication).
“Apakah pesan yang diterima
benar-benar berasal dari
pengirim yang benar?”

21. 4. Non Repudiation
 Layanan untuk
mencegah entitas yang
berkomunikasi
melakukan
penyangkalan, yaitu
pengirim pesan
menyangkal melakukan
pengiriman atau
penerima pesan
menyangkal telah
menerima pesan.

22. Kriptanalisis

23. Arti
 Kriptanalisis (cryptanalysis): ilmu dan seni
untuk memecahkan chiperteks menjadi
plainteks tanpa mengetahui kunci yang
digunakan.
 Pelakunya disebut kriptanalis
 (Perancang algoritma kriptografi:
kriptografer)
 Kriptanalisis merupakan “lawan”
Kriptografi

24. Arti (2)
 Kriptologi (cryptology): studi mengenai
kriptografi dan kriptanalisis.
Kriptologi
Kriptografi
Ilmu dan seni untuk menjaga
keamanan pesan
Kriptanalisis
Ilmu dan seni untuk
menmecahkan cipherteks

25. Terminologi
Persamaan kriptografer dan kriptanalis:
 Keduanya sama-sama menerjemahkan
cipherteks menjadi plainteks
Perbedaan kriptografer dan kriptanalis:
 Kriptografer bekerja atas legitimasi
pengirim atau penerima pesan
 Kriptanalis bekerja tanpa legitimasi
pengirim atau penerima pesan

26. Sejarah
 Teknik kriptanalisis sudah ada sejak abad
ke-9. oleh Abu Yusuf Yaqub Ibnu Ishaq
Ibnu As-Sabbah Ibnu 'Omran Ibnu Ismail
Al-Kindi, atau yang lebih dikenal sebagai
Al-Kindi

27. Analisis Al-Kindi
 Al-Kindi menulis buku tentang seni
memecahkan kode, berjudul
 ‘Risalah fi Istikhraj al-Mu'amma (Manuscript for
the Deciphering Cryptographic Messages)
 Al-Kindi menemukan frekuensi perulangan
huruf di dalam Al-Quran.
 kelak dinamakan analisis frekuensi.
 memecahkan cipherteks berdasarkan
frekuensi kemunculan karakter di dalam pesan

28. Cara Kerja Kriptografi

29. Unsur Kriptografi
 Sistem kriptografi (cryptosystem) memiliki
unsur sebagai berikut:
- algoritma kriptografi,
- plainteks,
- cipherteks,
- kunci.

30. Kategori Enkripsi Data
1. Pengiriman data melalui saluran
komunikasi (data encryption on motion).
2. Penyimpanan data di dalam disk storage
(data encryption at rest)

31. Data Encryption On Motion
 Sinyal yang ditransmisikan dalam
percakapan menggunakan handphone.
 Nomor PIN kartu ATM yang ditransmisikan
dari mesinATM ke komputer bank.
 Data terkirim dalam komunikasi BB

32. Data Encryption at Rest

33. Data Encryption at Rest (2)

34. Data Encryption at Rest (3)

35. Kriptografi Kunci Simetri
 Symmetric-key cryptography
 Kunci enkripsi = kunci dekripsi
 Istilah lainnya: kunci simetri, kunci privat,
kunci rahasia (secret key)
 Algoritma kriptografinya disebut algoritma
simetri

36. Contoh Alg. Kunci Simetri
 DES (Data Encyption Standard)
 Playfair
 Blowfish
 IDEA
 GOST
 Serpent
 RC2, RC4, Rc5, dll

37. Skema Alg. Kunci Simetri

38. Algoritma Kunci Asimetri
 Asymmetric-key cryptography
 Kunci enkripsi  kunci dekripsi
 Nama lain: kriptografi kunci-publik
 karena kunci enkripsi bersifat publik (public
key) sedangkan kunci dekripsi bersifat rahasia
(secret key atau private key).

39. Cara Kerja Kunci Asimetri
 Kriptografi kunci-publik dapat dapat
dianalogikan seperti kotak surat yang
terkunci dan memiliki lubang untuk
memasukkan surat.
 Kotak surat digembok dengan kunci. Kunci
hanya dimiliki oleh pemilik kotak surat.
 Setiap orang dapat memasukkan surat ke
dalam kotak surat tersebut,
 tetapi hanya pemilik kotak yang dapat membuka
kotak dan membaca surat di dalamnya karena ia
yang memiliki kunci.

40. Skema Alg. Kunci Asimetri

41. Keunggulan
 Keuntungan sistem ini:
1. Tidak ada kebutuhan untukmendistribusikan
kunci privat sebagaimana pada sistem kriptografi
simetri.
2. Kunci publik dapat dikirim ke penerimamelalui
saluran yang sama dengan saluran yang digunakan
untuk mengirim pesan. Saluran untuk mengirim
pesan umumnya tidak aman
3. Kedua, jumlah kunci dapat ditekan.

42. Algoritma Simetris
Kritografi Klasik

43. Kategori Algoritma
1. Cipher Substitusi (Substitution Ciphers)
2.CipherTransposisi (Transposition Ciphers)

44. Algoritma
Substitution Cipher: Monoalphabetic cipher

45. Monoalphabetic Cipher
Satu huruf di plainteks diganti dengan satu
huruf yang bersesuaian.
Jumlah kemungkinan susunan huruf-huruf
cipherteks yang dapat dibuat adalah
sebanyak 26!
atau sama dengan:
403.291.461.126.605.635.584.000.000
Contoh: Caesar Cipher

46. Caesar Cipher
 Contoh kasus:
 Tiap huruf alfabet digeser 3 huruf ke kanan
pi : A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
ci : D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
 Contoh:
Plainteks: AWASI ASTERIX DAN TEMANNYA OBELIX
Cipherteks: DZDVL DVWHULA GDQ WHPDQQBA REHOLA

47. Caesar wheel

48. Notasi Matematika
 Misalkan A = 0, B = 1, …, Z = 25, maka secara
matematis caesar cipher dirumuskan sebagai
berikut:
Enkripsi: ci = E(pi) = (pi + k) mod 26
Dekripsi: pi = D(ci) = (ci – k) mod 26
k= kunci rahasia

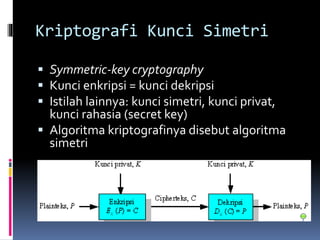
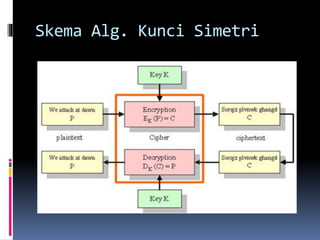
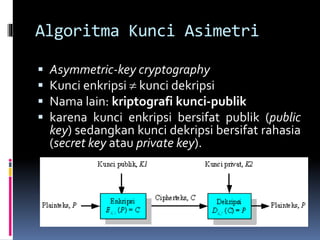
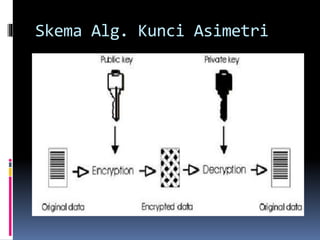
49. Contoh Source code dalam C
#include <stdio.h>
#include <conio.h>
#include <string.h>
#include <alloc.h>
struct Data {
int No; struct Data *Next;
};
void main() {
int a,b=0,c,d,e; char Word[100],Word1[100];
char Huruf[] = {'A','B','C','D','E','F','G','H','I','J','K','L‘,'M','N','O','P','Q','R','S','T','U','V','W','X‘,’Y','Z',’
‘};
struct Data *Head,*bantu,*THead,*bantu1;
printf("=== Caesar ChipherMethod ===n"); printf("Input Word :");
flushall(); gets(Word); flushall();
strcpy(Word1,strupr(Word));
Head = (struct Data*)malloc(sizeof(Data));
Head->Next = NULL; }

50. Kelemahan
 Caesar cipher mudah dipecahkan dengan
exhaustive key search karena jumlah kuncinya
sangat sedikit (hanya ada 26 kunci).

51. Monoalphabetic Cipher (2)
 Tabel substitusi dapat dibentuk secara acak:
 Atau dengan kata kunci
Atau menggunakan suatu kata kunci misalkan:
“we hope you enjoy this book”
Buang duplikasi huruf: wehopyunjtisbk
Sambung dengan huruf lain yang belum ada:
wehopyunjtisbkacdfglmqrvxz
 Tabel substitusi:
Contoh: Dapatkan ciphertext dari plaintext “Bandung”
51

52. Algoritma
Periodic Substition Cipher: Vigenere Cipher

53. Vigenere Cipher
 diciptakan oleh Blaise Vigenere pada abad ke-16
 Dalam proses enkripsi, ada kata kunci, sebutlah
k = k1 k2 k3 …km
 aturan dalam enkripsi adalah
Ek (p) = (p1+k1 p2+k2……pm+km) mod 26
 dekripsinya adalah :
Dk (c) =(c1-k1 c2-k2 ……cm-km)

54. Tabel Vigenere

55. Contoh
Contoh: (spasi dibuang)
P : KRIPTOGRAFIKLASIKDENGANCIPHERALFABETMAJEMUK
K : LAMPIONLAMPIONLAMPIONLAMPIONLAMPIONLAMPIONL
C : VR...
Perhitungan Enkripsi:
(K + L) mod 26 = (10 + 11) mod 26 = 21 = V
(R + A) mod 26 = (17 + 0) mod 26 = 17 = R
dst
Perhitungan Dekripsi:
(V – L) = (21 – 11) = 10 = K
Jika hasil pengurangan minus, baru dilakukan mod 26

56. Algoritma
Substitution Cipher: Polyalphabetic cipher

57. Penjelasan
 Monoalphabetic cipher: satu kunci untuk
semua huruf plaintext
 Polyalphabetic chiper dibuat dari sejumlah
monoalphabetic cipher, masing-masing
dengan kunci yang berbeda.
 Kebanyakan polyalphabetic cipher adalah
cipher substitusi periodik yang didasarkan
pada periodem.

58. Contoh
 Plaintext: merdekalah
 Kata kunci 1 (kk1): FIT
 Kata kunci 2 (kk2): UKM
 Kelompokkan plaintext dalam jumlah huruf yang
sama dan gunakan KK masing-masing yang
telah diekstrak (tidak mengandung huruf yang
sama)
merde kalah
kk1 kk2

59. Jawaban
 Untuk kelompok 1 (plaintext: merde)
Abcdef gh I j klmno pq r st uvwxyz
F I t abcdeghj kl mnopqr s uvwxyz
Diperoleh ciphertext: lbqab
 Untuk kelompok 2 (plaintext: kalah)
Abc def gh I j klmno pq r s t uvwxyz
ukmabcdef gh i j l no pq r s t vwxyz
Diperoleh ciphertext: huiue
Gabungan ciphertext: lbqab huiue

60. Algoritma
Transposition Cipher

61. Cara Kerja
 menggunakan huruf kunci yang diberi nama
dan nomor kolomsesuai dengan urutan huruf
pada huruf kunci tersebut.
 Nama lain untuk metode ini adalah
permutasi, karena transpose setiap
karakter di dalam teks sama dengan
mempermutasikan karakter-karakter
tersebut.

62. Contoh
 Enkripsi: baca secara vertikal
“FSORIAEAD ATGMVSNTU
KEIAEKMHN UKISRRAAG
LNNISIRB TOFUISAA
ALONTTNN”
 Dekripsi: baca secara vertikal
F SOR I A E A D
A TGMV S N T U
K E I A E K M H N
U K I SR R A A G
L N NI S I R B
T O FU I S A A
A LONT T N N

63. Contoh Kasus 2
 Sebagai contoh, huruf kunci adalah
MERDEKA,
 Diberikan penomoran untuk tiap huruf kata
kunci: 6253147
 digunakan untuk mengirimkan berita
“Fakultas Teknologi Informasi Universitas
Kristen Maranatha Bandung”.

64. Jawaban Kasus 2
 Enkripsi: salin dari urutan
kolomnomor kata kunci
mulai dari terkecil-terbesar
 LNNISIRB ATGMVSNTU
UKISRRAAG TOFUISAA
KEIAEKMHN FSORIAEAD
ALONTTNN
 Dekripsi: kata kunci dan
urutan nomor diketahui,
masukkan ciphertext secara
vertikal dari atas ke bawah

65. Algoritma
Playfair

66. Playfair
 Sandi Playfair digunakan olehTentara Inggris
pada saat Perang Boer II dan Perang Dunia I.
 Ditemukan oleh Sir Charles Wheatstone dan
Baron Lyon Playfair pada tanggal 26 Maret 1854.
 Playfair merupakan digraphs cipher,
 setiap proses enkripsi dilakukan pada setiap dua huruf.
 Misalkan plainteksnya “KRIPTOLOGI”, maka menjadi
“KR IP TO LO GI”.
 Playfair menggunakan tabel 5x5

67. Cara Kerja
 Semua alfabet kecuali J diletakkan ke dalam tabel.
Huruf J dianggap sama dengan huruf I, sebab huruf J
mempunyai frekuensi kemunculan yang paling kecil.
 Kunci yang digunakan berupa kata dan tidak ada
huruf sama yang berulang. Apabila kuncinya
“MATAHARI”, maka kunci yang digunakan adalah
“MATHRI”.
 Selanjutnya, kunci dimasukkan ke dalam tabel 5x5,
isian pertama adalah kunci, selanjutnya tulis huruf-huruf
berikutnya secara urut dari baris pertama
dahulu,
 bila huruf telah muncul, maka tidak dituliskan kembali.

68. Cara Kerja (2)

69. Proses Enkripsi
 Jika kedua huruf tidak terletak pada baris dan kolom yang sama, maka huruf pertama
menjadi huruf yang sebaris dengan huruf pertama dan sekolom dengan huruf kedua.
Huruf kedua menjadi huruf yang sebaris dengan huruf kedua dan sekolom dengan
huruf pertama. Contohnya, SA menjadi PH, BU menjadi EP.
 Jika kedua huruf terletak pada baris yang sama maka huruf pertama menjadi huruf
setelahnya dalam baris yang sama, demikian juga dengan huruf kedua. Jika terletak
pada baris kelima, maka menjadi baris pertama, dan sebaliknya. Arahnya tergantung
dari posisi huruf pertama dan kedua, pergeserannya ke arah huruf kedua. Contohnya,
AH menjadi TR, LK menjadi KG, BE menjadi CI.
 Jika kedua huruf terletak pada kolom yang sama maka huruf pertama menjadi huruf
setelahnya dalam kolom yang sama, demikian juga dengan huruf kedua. Jika terletak
pada kolom kelima, maka menjadi kolom pertama, dan sebaliknya. Arahnya
tergantung dari posisi huruf pertama dan kedua, pergeserannya ke arah huruf kedua.
Contohnya, DS menjadi LY, PA menjadi GW, DH menjadi HY.
 Jika kedua huruf sama, maka letakkan sebuah huruf di tengahnya (sesuai
kesepakatan).
 Jika jumlah huruf plainteks ganjil, maka tambahkan satu huruf pada akhirnya, seperti
pada aturan ke-4.

70. Proses Dekripsi
 Sedangkan proses dekripsinya adalah
kebalikan dari proses enkripsi.
 Contohnya,
 HR didekrip menjadi TH,
 BS didekrip menjadi DP,
 ZU didekrip menjadi RZ.

71. Contoh Soal
 Enkrip pesan “ATTACK TOMORROW”
menggunakan kunci dan tabel di atas.
 Jawab: Plainteksnya AT TA CK TO MO RR OW.
 Karena ada digraph RR, tambahkan sebuah
huruf, misalkan Q, maka plainteksnya
menjadi AT TA CK TO MO RQ RO WQ.
 Cipherteksnya : “TH AM KQ MQ IV TU MU
XP”

72. Latihan
 Enkripsi
 Plainteks: sekuritaskomputer
 Kunci: UKM
 Cipherteks:
 Dekripsi
 Cipherteks: PAQLFYKAFSQO
 Kunci: UKM
 Plainteks:

73. Algoritma
Affine

74. Algoritma Asimetris
RSA

75. Keterbatasan
 Tidak dapat mencegah aksi penyerangan
atau penghapusan data.
 dapat dikacaukan dengan memberikan
masukan berbeda atau modifikasi langsung
kepada file.
 Tersedianya secara luas teknik untuk men-dekode
sandi enkripsi.

76. Kesimpulan
Suatu algoritma kriptografi dikatakan aman
(computationally secure) bilamemenuhi tiga
kriteria berikut:
1. Persamaan matematis yang menggambarkan
operasi algoritma kriptografi sangat kompleks
sehingga algoritma tidak mungkin dipecahkan
secara analitik.
2. Biaya memecahkan cipherteks melampaui nilai
informasi yang terkandung di dalam cipherteks
3. Waktu untukmemecahkan cipherteks
melampaui lamanya waktu informasi tersebut
harus dijaga kerahasiaannya.

77. Referensi
 Bambang, Wilfridus. Materi Kuliah Sekuritas
Komputer, FIT - UK Maranatha, 2008.
 CEH v6.1 Module Course, 2009.
 Kelompok Studi Sandi –Yogyakarta, 2009.
 http://paulusharsono.wordpress.com, 2009.

79. Terima Kasih