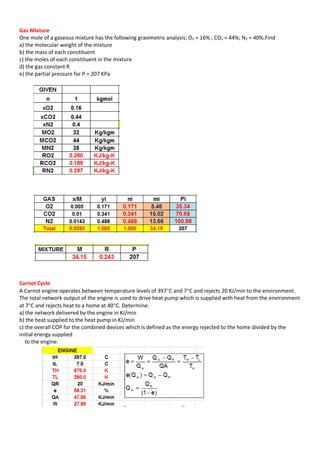
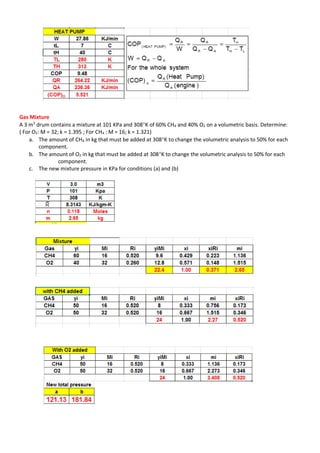
This document contains multiple problems involving ideal gas processes. The first problem describes a steady flow compressor handling nitrogen with known intake conditions and discharge pressure. It asks to determine the final temperature and work for two process types. The second problem involves air in a cylinder being compressed in a polytropic process with known initial and final pressures and temperatures. It asks to determine the work and heat transfer. The third problem describes a gas turbine expanding helium polytropically and asks to determine the final pressure, power produced, heat loss, and entropy change.

1. Processes (Ideal Gas)
A steady flow compressor handles 113.3 m3
/minof nitrogen ( M = 28; k = 1.399) measured at intake where P1= 97 KPa
and T1= 27
C. Discharge is at 311 KPa. The changes in KE and PE are negligible. For each of the following cases,
determine the final temperature and the work if the process is:
a) PVk
= C
b) PV = C
Given: V1 = 113.3/60 = 1.89 m3
sec ; P1 = 97 KPa ; T1 = 27 + 273 = 300 K
P2 = 311 KPa
a. K418










k
1k
1
2
12
P
P
TT
KW253-1
T
T
k1
VkP
W
1
211



















T1 = T2 = 300K
KW213.6-
P
P
lnVPW
2
1
11 
Processes (Ideal Gas)
Air is contained in a cylinder fitted with a frictionless piston. Initially the cylinder contains 500 L of air at 150 KPa and
20
C. The air is then compressed in a polytropic process ( PVn
= C) until the final pressure is 600 KPa, at which point
the temperature is 120
C. Determine the work W and the heat transfer Q. (R = 0.287 KJ/kg-K ; k = 1.4)
Given: V1 = 0.500 m3
; P1 = 150 KPa; T1 = 293K
P2 = 600 KPa; T2 = 393K
1.27n 


1
2
1
2
P
P
ln
T
T
ln
n
1n
kg892.0
RT
VP
m
1
11

KJ95

















 1
T
T
n1
VP
W
1
211
∆U = mCv(T2 – T1) = 64 KJ
Q = ∆U + W = 64 – 95 = - 31 KJ
Ideal Gas (Paddle Work)
A piston cylinder arrangement contains 0.02 m3
/min of air at 50
C and 400 KPa. Heat is added in the amount of 50 KJ
and work is done by a paddle wheel until the temperature reaches 700
C. If the pressure is held constant, how much
paddle wheel work must be added to the air. (R = 0.287 KJ/kg-K ; k = 1.4)
KJ1.8W
W-WUQ
KJ6.16)VV(PW
m06.0V
kg086.0m
mRTPV
Isobaric:Process
KJ50Q
KPa400P
K993T2K;32327350T
min
m
02.0V
P
P
12
3
2
1
3
1










Δ

2. KPa122.41P
3
6)(308)3.446(0.34
P
:bconditionFor
KPa80.28P
3
)(308)2.26(0.346
P
V
mRT
P
a;conditionforc)
kg3.4460.7962.65m
m
m2.65
m1.513
0.67
0.67x
0.33
24
0.50(16)
x
K-kg
KJ
0.346
24
8.3143
R
240.50(32)0.50(16)M
0.50y;0.50yb)
kg2.26.39-2.65m
negative.isitbecausemixturethefromremovedisCHsometherefore;kg0.39-m
m2.65
m1.137
0.33
m2.65
m1.137
x
0.67x
0.33
24
0.50(16)
x
K-kg
KJ
0.346
24
8.3143
R
240.50(32)0.50(16)M
0.50y;0.50yat
a)
kg1.5131.137-2.65m
kg1.137m
2.65
m
x
0.571
22.4
0.40(32)
x
0.429
22.4
0.60(16)
x
y
x
kg2.65m
0.371(308)
101(3)
m
mRTPV
K-kg
KJ
0.371
22.4
8.3143
R
22.40.40(32)0.60(16)M
40%y;60%y;K308T;KPa101P;m3V
:GIVEN
2
2
2
2
4
24
$
4
4
4
4
4
2
4
24
2
4
4
4
2
4
24
O
O
O
O
CH
OCH
4CH
CH
CH
CH
CH
CH
O
CH
OCH
O
CH
CH
CH
O
CH
i
i
OCH











































796.0
M
Mi
3
Ideal Gas Mixture
A 3 m3
drum contains a mixture at 101 KPa and 35C of 60% Methane (CH4) and 40% oxygen (O2) on a volumetric basis.
Determine the amount of oxygen that must be added at 35C to change the volumetric analysis to 50% of each
component. Determine also the new mixture pressure.
For CH 4: M = 16; k = 1.321
O2: R = 32 ; k = 1.395

3. Ideal Gas (Closed System)
Air from the discharge of a compressor enters a 1 m3
storage tank. The initial air pressure in the tank is 500 KPa and
the temperature is 600K. The tank cools, and the internal energy decreases 213 KJ/kg. Determine
a) the work done
b) the heat loss
c) the change of enthalpy
d) the final temperature
For Air
k = 1.4
R = 0.287
Kkg
KJ

K303T
)TT(mCh
KJ866)1.4(-618.5h
U
h
k
rejected)is(HeatKJ5.618-213)(9.2UmQ
kg9.2m
mRTPV
VolumettanCons0W
kg
KJ
-213U
K600T
KPa500P
m1V
2
12p
3












Δ
Δ
Δ
Δ
Δ
Δ
Entropy Change (Ideal Gas)
Calculate the change of entropy per kg of air when heated from 300
K to 600
K while the pressure drops from 400
Kpa to 300 KPa.
S = 0.78 KJ/kg-K)
Ideal Gas (Open System; Compressor)
An air compressor receives 20 m3
/min of air at 101.325 KPa and 20C and compresses it to 10 000 KPa in an isentropic
process. Calculate the power of the compressor.
Ideal Gas (Closed System)
A closed gaseous system undergoes a reversible process in which 40 KJ of heat are rejected and the volume changes
0.15 m3
to 0.60 m3
. The pressure is constant at 200 KPa. Determine the change of internal energy U in KJ.
Given:
Q = -40 KJ;
V1 = 0.15 m3
V2 = 0.60 m3
; P = 200 KPa
Solution:
Q = U + W ; W = P(V2 – V1)
W = 200(0.60 – 0.15) = 90 KJ
U = -40 – 90 = -130 KJ

4. Ideal Gas (Isentropic Process)
Air in a piston - cylinder occupies 0.12 m3
at 550 KPa. The air expands isentropically doing work on the piston until the
volume is 0.25 m3
. Determine the work W in KJ. For Air R = 0.287 KJ/kg-K and k = 1.4.
Given: V1 = 0.12 m3
; P1 = 550 KPa; V2 = 0.25 m3
KJ421
V
V
)k1(
VP
W
1k
2
11I


















Ideal Gas (Polytropic Process)
Air at 0.07 m3
and 4000 KPa is expanded in an engine cylinder and the pressure at the end of expansion is 320 KPa.
If the expansion is polytropic with PVn
= C where n = 1.35, find the final volume.
Given: V1 = 0.07 m3
; P1 = 4000 KPa ; P2 = 320 KPa ; PV1.35
= C
455.0
P
P
VV
VPVP
n
1
2
1
12
n
22
n
11










Ideal Gas
Gas at a pressure of 100 KPa, volume 0.20 m3
and temperature 300K, is compressed until the pressure is 320 KPa
and the volume is 0.09 cu.m.. Calculate the final temperature in K.
Given: P1 = 100 KPa; V1 = 0.20 m3
; T1 = 300K; P2 = 320 KPa; V2 = 0.09 m3
K4322T
T
VP
T
VP
2
22
1
11


Ideal Gas
Helium gas ( R=2.077 KJ/kg-K; k= 1.667) at 800 KPa and 300K occupies a volume of 0.30 m3
. Determine the mass of
helium in kg.
kg39.0m
mRTPV


Ideal Gas (Isometric Process)
A rigid container containing 25 kg of nitrogen gas at 298K receives heat and its temperature is increased to 370K.
Determine the amount of heat added in KJ.
For N2: R = 0.297 KJ/kgK; k = 1.399
Cv = 0.7444KJ/kg-K
Q = mCvT = 1334 KJ
Pure Substance (Isometric Process)
A 2 kg steam-water mixture at 1000 KPa and 90% quality (U = 2401.41 KJ/kg) is contained in a rigid tank. Heat is added
until the pressure rises to 3500 KPa and the temperature is 400C (U = 2926.4 KJ/kg). Determine the heat added in KJ.
Q = m(U2 – U1) = 1045 KJ
Ideal Gas
Calculate the pressure of 2 moles of air at 400K, with a total volume of 0.5 m3
.
MPa3.13P
TRnnMRTmRTPV


Ideal Gas
A 100 Liters oxygen tank use in a hospital has a pressure of 1 atmosphere and a temperature of 16C. For a molecular
weight of 32 kg/kgmol, determine the mass of oxygen in kilograms.
PV = mRT
T = 289K ; P = 101.325 KPa
m = 0.135 kg

5. Ideal Gas
An unknown gas has a mass of 1.5 kg and occupies 2.5 m3
while at a temperature of 300K and a pressure of 200 KPa.
Determine the gas constant for the gas in KJ/kg-K.
mT
PV
R  = 1.111 KJ/kg-K
Open System (Polytropic Process)
A gas turbine expands 50 kg/sec of helium (M = 4; k = 1.666) polytropically, PV1.8
= C, from 1000K and 500 KPa to
350K. Determine;
a. The final pressure in KPa
b. The power produced in KW
c. The heat loss in KW
d. The entropy change in KW/K
kw5-168,985.6)TT(mCh
0.523
n1
nk
CC
KW-16,989.85)TT(mCQ
KW151,995.80
n1
)TT(nmR
hQW
KPa627.14P
T
T
P
P
P
P
T
T
K350T
KPa500PK;1000T
(Open)TurbineGas:System
c)(PolytropiCPV:ocessPr
K-kg
KJ
08.2
M
8.3143
R
kg/sec50m
:Given
12p
vn
12n
12
2
1n
n
1
2
1
2
n
1n
1
2
1
2
2
11
1.8





































Δ
Δ
Open System
At one point in a pipeline the water speed is 3 m/sec and the gage pressure is 50 KPa. Find the gage pressure at a
second point in the line, 11 m lower than the first , if the pipe diameter at the second point is one half the first.

6. Ideal Gas (Open system; Nozzle)
Oxygen expands in a reversible adiabatic manner through a nozzle from an initial pressure and initial temperature and
with an initial velocity of 50 m/sec. There is a decrease of 38K in temperature across the nozzle. Determine
a. the exit velocity
b. for inlet conditions of 410 KPa and 320 K, find the exit pressure.
14.262P
K282T
38)T320(
38)TT(
T
T
PP;
T
T
P
P
P
P
T
T
sec
m
8.268v
395.1k;
K-kg
KJ
26.0
32
8.3143
R;
K-kg
KJ
918.0
1k
Rk
C
v)TT(C)1000(2v
)TT(C
)1000(2
vv
)TT(ChKE
0PE;0W;0Q
WPEKEhQ
2
2
2
21
1k
k
1
2
12
1k
k
1
2
1
2
k
1k
1
2
1
2
2
p
2
121p2
21p
2
1
2
2
12p










































ΔΔ
Δ
ΔΔΔ
Ideal Gas
A pressure in the cylinder in the figure varies in the following manner with volume, P = C/V2
. If the initial pressure is
500 KPa, initial volume is 0.05 m3
and the final pressure is 200 KPa, find the work done by the system.
3
1
2
1
2
1
2
2
22
2
11
2
2
3
11
m08.0V
P
P
V
CVPVP
CPV
KPa200P;m0.05VKPa;500P










Hydrostatic Pressure
A storage tank contains oil with a specific gravity of 0.88 and depth of 20 m. What is the hydrostatic pressure at the
bottom of the tank in kg/cm2
.
2
2
Bottom
cm
kg76.1
KPa325.101
cm
kg1.033
xKPa656.17220)81.9(88.00P 

7. Variation of Pressure
A hiker carrying a barometer that measures 101.3 KPa at the base of the mountain. The barometer reads 85 KPa at
the top of the mountain. The average air density is 1.21 kg/m3
. Determine the height of the mountain.
 
 
  m2.1373
g
PP1000
h
hhh
hh
1000
g
PP
1000
g
hP
21
12
1212







ρ
ρ
ρ
γ
ΔγΔ
Closed System
During the execution of a non-flow process by a system, the work per degree temperature increase is dW/dT = 170.9
J/K and the internal energy may be expressed as U = 27 + 0.68T Joules, a function of the temperature T in Kelvin.
Determine the heat in KJ if the temperature changes from 10C to 38C.
KJ48.0424Joules4804.24)1038(58.171)1T2T(58.171Q
dT58.171Q
dT58.171dQ
dT9.170dT68.0dQ
dWdUdQ
dT68.0dU
T68.027U
dT9.170dW
1
1








Pure Substance (Nozzle)
A nozzle receives 10 kg/sec of steam at 4 MPa and 260C (h = 2836.3 KJ/kg ;  = 51.74 x10-3 m3
/kg) and discharges it
at 1.4 MPa (h =2634.07 KJ/kg;  = 129.72 x 10-3 m3
/kg). If the velocity at inlet is negligible, find the diameter at exit
in cm.
cm5.10cm100x
v
m4
d
4
vd
4
vd
m
sec
kg
10
vA
m
sec
m
636v
-202.233.283607.2634h
)h)(1000(2v
0v
v)h)(1000(2v
h
)1000(2
vv
hKE
0PE;0W;0Q
WPEKEhQ
22
2
2
2
2
2
2
2
22
2
2
1
2
12
2
1
2
2













πρ
πρ
υ
π
υ
Δ
Δ
Δ
Δ
ΔΔ
Δ
ΔΔΔ

8. Properties of fluids
A 3 m diameter by 4.5 m height vertical tank is receiving water ( = 978 kg/m3) at the rate of 1.13 m3
/min and is
discharging through a 150 mm  with a constant velocity of 1.5 m/sec. At a given instant, the tank is half full. Find
the water level and the mass change in the tank 15 minutes later.
m27.1
)3(
4
0.9
waterofHeight
m0.9
978
8,799.9
tanktheinwaterofVolume
kg8,799.9mmmm
waterofmassinitialkg15,554.42
)2(4
)978)(5.4((3)
m
leavingkg23331.63
4
)978)(15)(60)(5.1()150.0(
m
enteringkg16,577.115)978(13.1m
2
3
2i1
2
i
2
2
1






π
Δ
π
π
Zeroth Law
An engineering student wants to cool 0.25 kg of Omni Cola (mostly water) initially at 20C by adding ice that is initially
at -20C. How much ice should be added so that the final temperature will be 0C with all the ice melted, if the heat
capacity of the container neglected.
 
kg06.0m
9.334)200(0935.2m)020)(187.4(25.0
QQ
ice
ice
iceCola



Zeroth Law
2.5 kg of brass of specific heat 0.39 KJ/kg-C at a temperature of 176C is dropped into a 1.2 liters of water at 14C.
Find the resulting temperature of the mixture. (At 14C density of water is 999 kg/m3
)
   
C35.40t
14t)187.4(999
1000
2.1
)t176)(39.0(5.2
QQ w aterBrass



Open system (Turbine)
Steam enters a turbine with a velocity of 1.5 m/sec and an enthalpy of 2093 KJ/kg and leaves with an enthalpy of 1977
KJ/kg and a velocity of 91.5 m/sec. Heat losses are 8 KCal/min and the steam flow rate is 27 kg/min. The inlet of the
turbine is 3.5 m higher than its outlet. What is the work output of the turbine if the mechanical losses is 15%.
(1 KCal = 4.187 KJ)
 
 
system)thebydone(workKW41.55.15)-(65.2)(1W
KW2.6515.451.9-52.256.0W
KW15.4505.3
60
27(9.81)
PE
KW1.9
)1000(2
(1.5)-(91.5)
60
27
KE
KW-52.220931977
60
27
h
RejectedKW56.0
60
)187.4(8
Q
WPEKEhQ
output
22


















Δ
Δ
Δ
ΔΔΔ

9. Open System (Compressor)
An air compressor handles 8.5 m3
/min of air with a density of 1.26 kg/m3
and a pressure of 101 KPaa and discharges
at 546 KPaa with a density of 4.86 kg/m3
. The changes in specific internal energy across the compressor is 82 KJ/kg
and the heat loss by cooling is 24 KJ/kg. Neglecting changes in kinetic and potential energies, find the work in KW.
 
kg
KJ
-138.2PEKEh-QW
loss)(heat
kg
KJ
24Q
kg
KJ
19.1148219.32h
kg
KJ
19.32
26.1
101
86.4
546P
)P(
0PE
kg
KJ
82U
U)P(h
WPEKEhQ
sec
kg
18.026.1
60
5.8
m
system)(0penCompressor:System















ΔΔΔ
Δ
ρ
ΔυΔ
Δ
Δ
ΔυΔΔ
ΔΔΔ
Closed system (Piston in cylinder)
Four kilograms of a certain gas is contained within a piston–cylinder assembly. The gas undergoes a process for
which the pressure - volume relationship is PV1.5
= C. The initial pressure is 300 KPa, the initial volume is 0.10 m3
, and
the final volume is 0.2 m3
. The change in specific internal energy of the gas in the process is U = - 4.6 kJ/kg. There
are no significant changes in kinetic or potential energy. Determine the net heat transfer for the process, in kJ.
KJ35.97Q
KJ4.184.6(4)U
KJ57.17W
KPa07.106P
VPVP
n1
VP-VP
PdVW
WUQ
kg
KJ
4.6U;m0.20V;m0.10VKPa;300P
(Closed)Cylinder-Piston:System
2
n
11
n
22
1122
3
2
3
11










Δ
Δ
Δ
Entropy Change
Calculate the change of entropy per kg of air (R = 0.287 KJ/kg-K; k = 1.4) when heated from 300K to 600K while the
pressure drops from 400 KPa to 300 KPa.
K-kg
KJ
78.0S
K-kg
KJ
0045.1
1k
Rk
CP




Δ

10. Law of Conservation of Mass
Steam at 1 MPa, 300°C flows through a 30 cm diameter pipe with an average velocity of 10 m/s. Determine mass flow
rate of this steam. (Density at 1 MPa and 300C = 3.875 kg/m3
)
   
sec
kg
74.21030.0
4
875.3m
Avm
2








π
ρ
Closed System (Piston in Cylinder)
Air is compressed in a piston-cylinder device. Using constant specific heats and treating the process as internally
reversible, determine the amount of work required to compress this air from 100 KPa, 27°C to 2000 KPa, 706°C.
kg
KJ
8.266W
652.1n
P
P
ln
T
T
ln
n
1n
V
V
ln
P
P
ln
n
logarithmofLawsgsinU
P
P
T
T
P
P
V
V
VPVP
n1
)TT(R
n1
VP-VP
PdVW
WUQ
CPV:Process
(closed)Cylinder-Piston:System
1
2
1
2
1
2
2
1
n
1n
1
2
1
2
2
1
n
1
2
n
22
n
11
121122
n





































Δ
Open System (Nozzle)
Air enters the after burner nozzle of a jet fighter at 427°C with a velocity of 100 m/s. It leaves this adiabatic nozzle at
377°C. Assuming that the air specific heats do not change with temperature, determine the velocity at the nozzle exit.
sec
m
3.332v
sec
m
100v
C377T
C427T
0045.1C
v)TT(C)1000(2v
)TT(C
)1000(2
vv
)TT(ChKE
0PE;0W;0Q
WPEKEhQ
2
1
2
1
p
2
121p2
21p
2
1
2
2
12p











ΔΔ
Δ
ΔΔΔ

11. Gas Mixture
One mole of a gaseous mixture has the following gravimetric analysis: O2 = 16% ; CO2 = 44% ; N2 = 40%. Find
a. the molecular weight of the mixture
b. the mass of each constituents
c. the moles of each constituent in the mixture
Formulas
n
ni
yi
M
3143.8
R
n
m
MyiMiM
m
mi
xi
Mi
xi
Mi
xi
yi




Σ
Σ
Open System (Nozzle)
Air enter the nozzle as shown at a pressure of 2700 KPa at a velocity of 30 m/sec and with an enthalpy of 923 KJ/kg,
and leaves with a pressure of 700 KPa and enthalpy of 660 KJ/kg. If the heat loss is 0.96 KJ/kg, find the exit velocity in
m/sec if the mass flow rate is 0.2 kg/sec.
 
sec
m
6.724v
sec
m
30v
kg
KJ
-263923)-(660h
vh-Q2000v
h-Q
2000
vv
h-QKE
0PE;0W
kg
KJ
-0.96Q
WPEKEhQ
(Open)Nozzle:System
2
1
2
12
2
1
2
2










Δ
Δ
Δ
ΔΔ
Δ
ΔΔΔ
Ideal Gas
A certain perfect gas of mass 0.1 kg occupies a volume of 0.03 m3
at a pressure of 700 KPa and a temperature of 131C.
The gas is allowed to expand until the pressure is 100 KPa and the final volume is 0.02 m3
. Calculate;
a) the molecular weight of the gas
b) the final temperature

12. K5.38T
T)52.0(1.0)02.0(100
kg
kg
16
52.0
3143.8
M
K-kg
KJ
52.0R
)273131(R1.0)03.0(700
mRTPV
mol






Force
10 liters of an incompressible liquid exert a force of 20 N at the earth’s surface. What force would 2.3 Liters of this
liquid exert on the surface of the moon? The gravitational acceleration on the surface of the moon is 1.67 m/sec2
.
N80.067.1)9.203(0023.0F
m
kg
9.203
)81.9(01.020
maF
01.0m
Vm;
V
m
m01.0V
Moon
3
3







ρ
ρ
ρ
ρρ
Manometers
A closed tank contains compressed air and oil (S = 0.90) as shown in the figure.a U – tube manometer using mercury
(S = 13.6) is connected to the tank as shown. For column heights h1 = 90 cm; h2 = 15 cm and h3 = 22 cm, determine
the pressure reading of the gage.
hP ΔγΔ 
KPa20.08P
P)90.0)(81.9(90.0)15.0)(81.9(90.0)22.0)(81.9(6.130
gage
gage



13. Manometer
In the figure pipe A contains carbon tetrachloride (S = 1.60) and the closed storage tank B contains a salt brine
(S =1.15). Determine the air pressure in tank B in KPa if the gage pressure in pipe A is 1.75 kg/cm2
.
gageKPa08.154P
P9.81)1.2(1.15)(-15)(9.81)(0.914)(1.6)(9.81)(0.914)(1.-171.65
m914.0ft3
KPa65.171
033.1
)325.101(
75.1P
B
B
A




Ideal Gas (Isothermal Process)
Air which is initially at 120 KPa and 320K occupies 0.11 m3
. It is compressed isothermally until the volume is halved
and then compressed it at constant pressure until the volume decreases to ¼ of the initial volume. Sketch the process
on the PV and TS diagrams. Then determine the pressure, the volume and temperature in each state.
K160T
V
V
T
T
m0275.0
4
0.11
V
KPa240PP
(Isobaric)3to2At
K320TKPa;240
V
VP
P
m055.0
2
0.11
V
l)(Isorherma2to1At
kg144.0
)320(287.0
)11.0(120
m
mRTPV
m0.11VK;320TKPa;120P
1.4kK)-KJ/kg0.287(RAir:Fluid
VPVP:IsothermalocessPr
3
2
3
2
3
3
3
3
2
2
11
2
3
2
3
111
2211
2












14. Gas MIxture
One mole of a gaseous mixture has the following gravimetric analysis; O2 = 16% ; CO2 = 44%; N2 = 40%.Find
a) the molecular weight of the mixture
b) the mass of each constituent
c) the moles of each constituent in the mixture
d) the gas constant R
e) the partial pressure for P = 207 KPa
Carnot Cycle
A Carnot engine operates between temperature levels of 397C and 7C and rejects 20 KJ/min to the environment.
The total network output of the engine is used to drive heat pump which is supplied with heat from the environment
at 7C and rejects heat to a home at 40C. Determine:
a) the network delivered by the engine in KJ/min
b) the heat supplied to the heat pump in KJ/min
c) the overall COP for the combined devices which is defined as the energy rejected to the home divided by the
initial energy supplied
to the engine.

15. Gas Mixture
A 3 m3
drum contains a mixture at 101 KPa and 308K of 60% CH4 and 40% O2 on a volumetric basis. Determine:
( For O2: M = 32; k = 1.395 ; For CH4 : M = 16; k = 1.321)
a. The amount of CH4 in kg that must be added at 308K to change the volumetric analysis to 50% for each
component.
b. The amount of O2 in kg that must be added at 308K to change the volumetric analysis to 50% for each
component.
c. The new mixture pressure in KPa for conditions (a) and (b)

16. kg408.30.7582.65m
kg758.0
667.01
515.1)65.2(667.0
my
667.0
my65.2
my515.1
x
addedO2With
kg27.238.65.2m
756.038.0136.1mCH4
mixturethefromremovedisCH4therfore
kg38.0
333.1
136.1)65.2)(333.0(
mx
mx136.1)65.2)(333.0(mx333.0
mx65.2
mx136.1
333.
mx65.2
mx136.1
x
removedoraddedCH4With
O2
4CH






















Diesel Cycle
An air standard diesel cycle has a compression ratio of 18 and the heat transferred is 1800 KJ/kg. At the beginning of
the compression process the pressure is 100 KPa and the temperature is 15C. For 1kg of air, determine
The entropy change during isobaric heat addition
The temperature at the start of heat rejection
The work in KJ
The thermal efficiency
The mean effective pressure in KPa
 
   
KPa2.1362P
m781.0V
P
mRT
V;
P
mRT
V
VVV
V
W
Pm
KJ4.1063Q-QW
%1.59
Q
Q-Q
e
KJ6.736)TT(mCQ
K61.1314T
T
T
lnmC)SS(SS
K
KJ
0894.1
T
T
lnmCSS
K1.2707T
mC
Q
T
)T-(TmCQ
KPa8.571918100rPP
K915rTT
m
3
D
2
2
2
1
1
1
21D
D
RA
A
RA
14vR
4
4
1
v2341
2
3
p23
2
p
A
3
23pA
4.1k
12
1k
12
















For Air
k = 1.4
R = 0.287 KJ/kg-K

17.  
%71.57100%x
Q
W
e
KJ/kg34.477Q-QW
KJ/kg76.349Q
TTCQ
A
RA
R
14VR




Diesel Cycle
In the air standard diesel cycle, the air is compressed isentropically from 26C and 105 KPa to 3700 KPa. The entropy
change during heat rejection is -0.6939 KJ/kg-K. Determine
a) the heat added per kg
b) the thermal efficiency
c) the maximum temperature
d) the temperature at the start of heat rejection
P
V
1
2 3
4
S = C
S = C
T
S
1
2
3
4
V = C
P = C
QR
QA
Given:
T1 = 26 + 273 = 299 K
P1 = 105 KPa
P2 = P3 = 3700 KPa
S1 – S4 = -0.6939 KJ/kg-K
S3 – S2 = 0.6939 KJ/kg-K
 
 
K47.786T
299
T
e
T
T
lnCS-S
KJ/kg1.827T-TCQ
K71.1650T
3.827
T
e
827.3
T
ln0045.16939.0
T
T
lnmCSSS
K3.827T
P
P
T
T
4
40.7175
0.6939
1
4
v14
23pA
3
31.0045
0.6939
3
2
3
p23
2
k
1-k
1
2
1
2

















18.  
 
 
KPa9.480P
T0026.0
T25.1
V
W
P
11.eqT25.1W
T315.254.0W
10.eqT315.2Q
163.239.51T7175.0Q
T163.2T39.57175.0Q
)TT(CQ
9.eqeQW
Q
W
e
m
1
1
D
m
1
1
1A
A
11A
23vA
A
A










 
 
 
 
 
 
 
8.eqT0026.0V
188.6T00045.0V
7.eqT00045.0
91.1383
T163.2287.0
P
RT
6.eq1rV
rV
5.eqr
r
4.eqV
3.eqT49.2rT
r
T
T
2.eqT39.5
P
P
TT
1.eqT163.2rTT
%5454.0
r
1
1e
KPa91.138388.693P
r
P
P
V
V
V
V
r
88.6r
17.
17.1
c
c1
r
1D
1D
1
1
2
2
2
2D
22D
21
2
1
21D
1
k1
31k
3
4
1
2
3
23
1
1k
12
1k
4.1
2
k
1
2
3
4
2
1



































Otto Cycle
For an ideal Otto engine with 17% clearance and an initial pressure of 93 Kpa, determine the pressure at the end of
compression. If the pressure at the end of constant volume heating is 3448 KPa, what is the mean effective pressure.
P
V
T
S
1
1
2
2
3
3
4 4
S = C
S = C
V = C
V = C
QA
QR
Given:
c= 0.17
P1 = 93 KPa
P3 = 3448 KPa

19. 488.0y
341.0y
171.0y
0293.0
28
40.
44
44.
32
16.0
Mi
xi
Mi
xi
Mi
xi
yi
2
2
2
N
CO
O






Carnot Heat Pump
A Carnot engine operates between temperature levels of 397C and 7C and rejects 20 KJ/min to the environment. The
total network output of the engine is used to drive heat pump which is supplied with heat from the environment at 7C
and rejects heat to a home at 40C. Determine:
a) the network delivered by the engine in KJ/min
b) the heat supplied to the heat pump in KJ/min
c) the overall COP for the combined devices which is defined as the energy rejected to the home divided
by the initial energy supplied to the engine.
Carnot Reverse Cycle
A reversed Carnot cycle is used for refrigeration and rejects 1000 KW of heat at 340 K while receiving heat at 250 K.
Determine:
a) the COP
b) the power required in KW
c) the refrigerating capacity in Tons
Gas Mixture
One mole of a gaseous mixture has the following gravimetric analysis; O2 = 16% ; CO2 = 44%; N2 = 40%.Find a)
the molecular weight of the mixture b) the mass of each constituent c) the moles of each constituent in the mixture
d) the gas constant R e) the partial pressure for P = 207 KPa
Isentropic Process
A blower compresses 0.02 m3
/sec of gaseous mixture that has the following volumetric analysis: CO2 = 11% ; O2 =
8% ; CO = 1% ; N2 = 80% ; from 101 Kpa and 27 C to 180 KPa. Assuming the compression to be isentropic, find the
work in KW.
For CO : For O : For CO: For N :
M =44 M = 32 M = 28 M = 28
K = 1.288 K = 1.295 K = 1.399 K = 1.399
Gas Mixture
A 0.23 m3 drum contains a gaseous mixture of CO2 and CH4 each 50% by mass at P = 689 KPa, 38C; 1 kg of O2
are added to the drum with the mixture temperature remaining at 38C. For the final mixture, find;
a) the gravimetric analysis
b) the volumetric analysis
c) the Cp (For CO2: k = 1.288; CH4: k = 1.321; O2: k = 1.395)

20. d) the total pressure
Gas Mixture
A gaseous mixture composed of 25 kg of N2, 3.6 kg of H2, and 60 kg of CO2 is at 200 KPa, 50C. Find the respective
partial pressures and compute the volume of each component at its own partial pressure and 50C.
Given:
mN2 = 25 kg ; mH2 = 3.6 kg ; mCO2 = 60 kg
m = 25 + 3.6 + 60 = 88.6 kg
xN2 = 0.282 ; xH2 = 0.041 ; xCO2 = 0.678
P = 200 KPa ; T = 323 K
PN2 = .219(200) = 43.8 KPa
PH2 = .446(200) = 89.2 KPa
PCO2 = 0.335(200) = 67 KPa
Gas Mixture
Assume 2 kg of O2 are mixed with 3 kg of an unknown gas. The resulting mixture occupies a volume of 1.2 m3
at 276
KPa and 65C. Determine
a) R and M of the unknown gas constituent
b) the volumetric analysis
c) the partial pressures
Given;
mO2 = 2 kg; mx = 3 kg
V = 1.2 m3
; P = 276 KPa; T = 338 K
a)
m = 5 kg
xO2 = 0.40 ; xx = 0.60
R = 0.1361 KJ/kg-K
R = .40(0.26) + 0.60(Rx)
Rx = 0.535 KJ/kg-K
Mx = 15.54 kg/kgm
b)
yO2 = 0.245 ; yx = 0.755
c) PO2 = .245(276) = 67.62 KPa ; Px = 0.755(276) = 208.38 KPa
335.0y
446.0y
219.0y
046.0
44
678.
2
041.
28
282.0
Mi
xi
Mi
xi
Mi
xi
yi
2
2
2
CO
H
N






P
Pi
yi 
3
CO
3
H
3
N
iiiii
m67.54
67
)323)(189.0(60
V
m23.54
2.89
)323)(16.4(6.3
V
m76.54
8.43
)323(297.0(25
V
TRmVP
2
2
2




mRTPV 
0511.0
54.15
60.
32
40.
M
x
i
i


21. KPa122.41P
3
6)(308)3.446(0.34
P
:bconditionFor
KPa80.28P
3
)(308)2.26(0.346
P
V
mRT
P
a;conditionforc)
kg3.4460.7962.65m
m
m2.65
m1.513
0.67
0.67x
0.33
24
0.50(16)
x
K-kg
KJ
0.346
24
8.3143
R
240.50(32)0.50(16)M
0.50y;0.50yb)
kg2.26.39-2.65m
negative.isitbecausemixturethefromremovedisCHsometherefore;kg0.39-m
m2.65
m1.137
0.33
m2.65
m1.137
x
0.67x
0.33
24
0.50(16)
x
K-kg
KJ
0.346
24
8.3143
R
240.50(32)0.50(16)M
0.50y;0.50yat
a)
kg1.5131.137-2.65m
kg1.137m
2.65
m
x
0.571
22.4
0.40(32)
x
0.429
22.4
0.60(16)
x
y
x
kg2.65m
0.371(308)
101(3)
m
mRTPV
K-kg
KJ
0.371
22.4
8.3143
R
22.40.40(32)0.60(16)M
40%y;60%y;K308T;KPa101P;m3V
:GIVEN
2
2
2
2
4
24
$
4
4
4
4
4
2
4
24
2
4
4
4
2
4
24
O
O
O
O
CH
OCH
4CH
CH
CH
CH
CH
CH
O
CH
OCH
O
CH
CH
CH
O
CH
i
i
OCH











































796.0
M
Mi
3
Gas Mixture
A 3 m3
drum contains a mixture at 101 KPa and 308K of 60% CH4 and 40% O2 on a volumetric basis.
Determine: ( For O2: M = 32; k = 1.395 ; For CH4 : M = 16; k = 1.321)
a) The amount of CH4 in kg that must be added at 308K to change the volumetric analysis to
50% for each component.
b) The amount of O2 in kg that must be added at 308K to change the volumetric analysis to
50% for each component.
c) The new mixture pressure in KPa for conditions (a) and (b)
By: ENGR. YURI G. MELLIZA