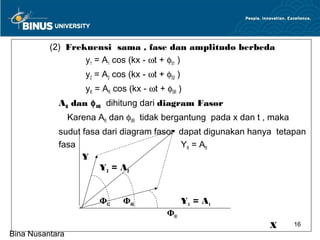
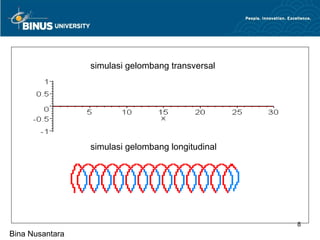
Pertemuan ini membahas pengertian gelombang secara umum, persamaan gelombang, kecepatan rambatan gelombang dalam medium, dan energi gelombang. Topik utama mencakup macam-macam gelombang, parameter gelombang, kecepatan gelombang, energi dan intensitas gelombang, serta superposisi gelombang."

2. Matakuliah : K0252 / Fisika
Dasar II
Tahun : 2007
GELOMBANG
PERTEMUAN 01

3. Gelombang
Pertemuan 01
Pertemuan ini membahas beberapa masalah seperti pengertian
gelombang secara umum , persamaan diferensial /persamaan
gelombang , kecepatan rambatan gelombang dalam suatu medium .
beserta energi gelombang . Persyaratan untuk dapat mengikuti
pembahasan dalam bab ini adalah : Mahasiswa sudah fasih
dalam kalkulus ( khususnya persamaan diferensial
parsial , diferensial / integral ) dan ilmu ukur sudut.
DEFINISI GELOMBANG : Gelombang merupakan rambatan
gang - .
guan dalam suatu medium
1. Macam-macam gelombang
▪ Berdasarkan medium tempat gelombang merambat .
3
Bina Nusantara

4. • Gelombang mekanik
- Gelombang mekanik hanya merambat dalam medium elastis .
Contoh : Gelombang bunyi , gelombang pada tali , gelombang pada
permukaan air dan lain-lain .
­ Gelombang elektromagnetik
Gelombang ini berhubungan dengan medan listrik dan medan magnet .
Dalam rambatannya tidak memerlukan medium .
Contoh : Gelombang radio , cahaya , dan lain-lain.
• Berdasarkan arah getaran medium
- Gelombang transversal
Gelombang yang arah getarannya tegak lurus pada arah rambatan .
- Gelombang longitudinal .
Gelombang yang arah getarannya searah dengan arah rambatan
gelombang.
4
Bina Nusantara

5. 2. Bentuk gelombang
- Gelombang denyut (Pulsa)
Gangguan tunggal yang merambat dalam suatu medium
- Gelombang harmonik (gelombang selaras)
Gangguan dalam bentuk yang sama berulang secara periodik .
3. Komponen gelombang
Gelombang terdiri dari
- Rambatan gangguan / rambatan gelombang
- Getaran medium / getaran gelombang
4. Parameter gelombang
• Amplitudo = Y(=A) = ym = simpangan maksimum
• Satuan : satuan panjang ( m , cm , mm , .. )
5
Bina Nusantara

6. • Panjang gelombang = λ ; jarak antara dua titik yang berbeda fase 2π
Satuan : satuan panjang ( m , cm , mm , )
• Periode = T = Waktu Getar ; Satuan : sekon
• Frekuensi = f = 1/T : banyak getaran per sekon ; Satuan : Hz , atau
cps
• Kecepatan rambatan gelombang = V (C) = λ f ; Satuan : m / s.
• Bilangan gelombang = k = banyaknya gelombang per satuan panjang
• Frekuensi sudut = ω = 2πf ; Satuan : radian per sekon
▪ Konstanta fase : Φ 0 = fase awal ; Satuan : radian
∂2y 1 ∂2y
5. Rumusan Gelombang
= 2 ; y = simpangan , x = arah
1. Persamaan2 diferensial gelombang ramba tan (01)
∂x2
C ∂t
6
Bina Nusantara

7. 2. Persamaan gelombang
Jawaban umum dari persamaan diferensial gelombang adalah ;
Y (x , t) = f ( x ± C t )
y (x , t) = f ( x + V t ) ; gelombang merambat ke kiri.
y (x , t) = f ( x - C t ) ; gelombang merambat ke kanan
Untuk gelombang harmonik jawaban dari persamaan di atas dapat
dinyatakan sebagai fungsi cosinus (cos) ataupun fungsi sinus (sin)
sebagai berikut :
y(x.t) = Y sin [k (x - Vt) atau
y(x.t) = Y cos [k(x - Vt) ; k = konstanta rambatan
gelombang
Penyelesaian dari (01) menghasilkan :
Y(x,t) = Ym sin (kx - ωt + Φ 0) …………………………….
(02)
7
Ym dan Φ 0 dari syarat awal ( t = 0 dan Y = 0)
Bina Nusantara

8. simulasi gelombang transversal
simulasi gelombang longitudinal
8
Bina Nusantara

9. 6. Kecepatan gelombang
(A). Kecepatan gelombang pada dawai
Gelombang merambat sepanjang tali
Y
FY ‘ S = gaya tarik [N]
ds
α
S FY
X dX X + dX
X
Tinjau bagian tali antara x dan x + dx , yaitu elemen busur d s .
Dalam keadaan setimbang massanya = μ dX , μ = massa/panjang
Gaya yang bekerja padanya : ∂ F
y
Fy ' - Fy = dx
∂x
9
Bina Nusantara

10. Menurut hukum Newtom II : F = massa x percepatan →
∂Fy ∂2 y
dx = µ dx g 2
∂x ∂t
Untuk α << maka sin α ≈ tg α → Fy sin α ≈ S tg α ≈ S ∂y/∂x
maka : 2
∂ y
2
∂y
S =µ 2 ⇒
∂x 2 ∂t
∂ 2 y 1 ∂y 2
= 2 2 Persamaan diferensial gelombang
∂x 2
C ∂t
S
C= , kecepa tan gelombang pada dawai ...................(03)
µ
http://www.physics.louisville.edu/public/courses/phys111/dav
10
Bina Nusantara

11. (B). Kecepatan gelombang dalam benda
B
C=
(04) ρ
B = modulus benda [N/m2] , ρ = kerapatan benda
[kg/m3] m
Y
(C). Kecepatan gelombang dalam benda tegar
V=
ρ
(05)
Y = modulus Young [N/m2]
(D). Kecepatan gelombang dalam gas/udara
V sempurna= γ RT
= γ P :
Untuk gas ρ M
11
Bina Nusantara

12. .M = berat molekul , T = suhu gas/udara 0K
P = tekanan dalam [N/m2= Pascal]
R = konstanta gas universal [8315 J/(kmol. k)]
γ = konstanta Laplace = CP /CV
7. Energi dan Intensitas Gelombang
Gelombang dalam rambatannya mengangkut energi
Y
F Ftrans = - F(∂y / ∂x )
FX dawai
X
12
Bina Nusantara
Ftrans = F(∂y/∂x)

13. • Tenaga yang dipindahkan persatuan waktu :
∂y ∂y
.P = D (Daya) = Ftrans • U = - g
F
∂x ∂t
U = Kecepatan partikel dawai menyimpang ke arah
transversal
• Untuk gelombang berbentuk :
Y (x.t) = Ym sin ( kx - ωt )
maka : P = ym 2 k ω F cos2( kx - ωt )
Tenaga rata-rata yang dipindahkan dalam T detik
adalah : P = 2 π 2 y2 f2 µ V , µ = massa/satuan
1
panjang cos 2 ( k x − ω t ) =
2
dimana cos ( kx - ωt )
2
13
Bina Nusantara

14. Untuk benda berdimensi tiga maka μ diganti dengan ρ
A , .
sehingga P = 2π 2 y 2 f 2 ρ A V
m
(07)
8. Intensitas Gelombang
Jumlah energi yang dipindahkan persatuan luas persatuan
P
=
waktu (daya Iper satuan luas) disebut intersitas
gelombang A
(08)
Untuk gelombang sferis ( muka gelombang berbentuk
14
bola )
Bina Nusantara

15. I1  R 2 
2
=
(09) I2  R 2 ÷
 ÷
 1 
9. SUPERPOSISI GELOMBANG
Dua atau lebih gelombang yang sejenis menjalar dalam suatu
medium pada tempat dan waktu yang sama, maka gangguan total
pada medium adalah jumlah dari masing-masing gelombang
yR (x,t) = y1 (x,t) + y2 (x,t) + y3 (x,t)
(10)
Untuk 2 gelombang sinus menjalar dalam arah dan kecepatan
yang
sama :
(1). Frekuensi dan amplitudo sama, fase berbeda
y1 = A1 sin (kx- ωt + φ 01 )
y2 = A2 sin (kx- ωt + φ 02 ) , A1 = A2 = A → 15
Bina NusantaraR = y1 + y2 →
y

16. (2) Frekuensi sama , fase dan amplitudo berbeda
y1 = A1 cos (kx - ωt + φ01 )
y2 = A2 cos (kx - ωt + φ02 )
yR = AR cos (kx - ωt + φ0R )
AR dan φ 0R dihitung dari diagram Fasor
Karena AR dan φ0R tidak bergantung pada x dan t , maka
sudut fasa dari diagram fasor dapat digunakan hanya tetapan
fasa YR = AR
Y
Y2 = A 2
Φ02 Φ0R Y 1 = A1
Φ01
X 16
Bina Nusantara

17. AR = A1 + A 2 + 2 A1 A 2 Cos( φ01 -φ02 )
2 2
2
A1Sinφ + A 2Sinφ2
tan φ0 R = 1
A1Cosφ1 + A 2Cosφ2
Contoh : y1 = ym sin (kx – ωt – Φ )
y2 = ym sin (kx – ωt)
→ yR = y1 + y 2
= ym { 2 sin (kx – ωt – Φ/2).cos Φ/2}
= 2ymcos Φ/2 sin (kx – ωt – Φ/2)
Amplitudo gelombang resultan AR = 2ymcos Φ/2
17
Bina Nusantara

18. Contoh soal :
Salah satu ujung sebuah pipa karet tergantung melalui
suatu digantunkan benda bermassa 2 kg . Panjang pipa
karet ini 8 m dan massanya 0.6 kg . Berapakah kecepatan
gelombang transversal dalam pipa ini.
Jawaban :
- Berat benda ,W, yang tergantung pada pipa karet :
W = m g = 2 kg x 9.8 m/s2 = 19.6 N
- Massa pipa karet per satuan panjang , μ :
μ = 0.6 kg/ 8m = 0.075 kgm
- Kecepatan gelombang , V , dalam pipa karet :
V = √(S/m) = √(19.6 N/(0.076 kg/m)) = 16 m/s
Jadi kecepatan gelombang dalam pipa karet V = 16 m/s
18
Bina Nusantara

19. simulasi gelombang pada permukaan air
19
Bina Nusantara

20. 20
Bina Nusantara

21. 21
Bina Nusantara