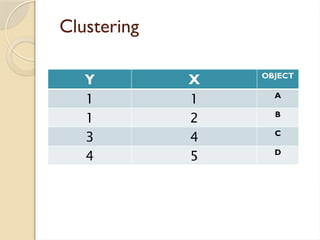
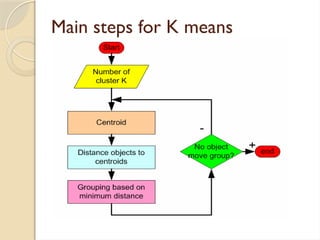
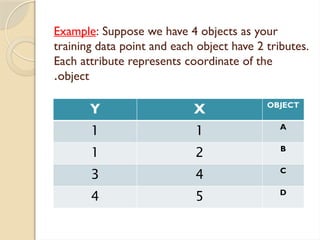
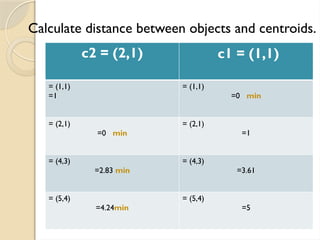
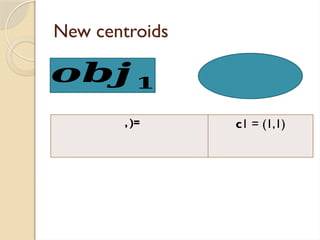
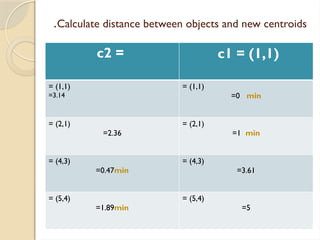
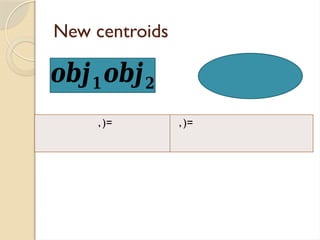
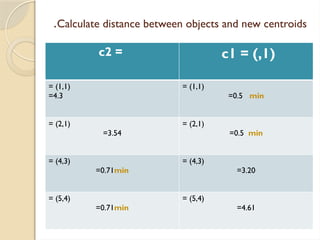
Clustering is an unsupervised learning process that partitions data into similar subsets, with methods including partitioning and hierarchical approaches. K-means clustering is a centroid-based algorithm that groups data points into k clusters by minimizing the distance within clusters, using distance metrics like Euclidean and Manhattan distances. Key steps in this process involve selecting initial centroids, assigning data points to clusters based on distance, and recalculating centroids until convergence.

1. Clustering
 Clustering: the process of portioning a set of
data objects into subsets (clusters) where
objects in a cluster are similar to one , yet
dissimilar to objects in other clusters.
 Considered as unsupervised learning: no
predefined classes (learning by observation
vs learning by examples)
 Descriptive data mining

2. Clustering
Y X OBJECT
1 1 A
1 2 B
3 4 C
4 5 D

3. Types of Clustering
:
 Partitioning approach: construct
various portions and then evaluate
them by some criterion (i.e.
minimize the sum of square errors).
 Hierarchical approach: create a
hierarchal decomposition of the set
of data using some criterion.

4. Partitioning approach
 Partitioning methods:: Partioning a
dataset D of n objects into a set of k
clusters.
 A centroid-based partitioning
technique uses the centroid of a
cluster, Ci , to represent that cluster.
 The centroid can be defined in
various ways such as by the mean
or medoid of the objects (or points)

5. What is K-Means Clustering
?
 It is an algorithm to group your objects
based on attributes/features into K
number of group.
 K is positive integer number.
 Cluster representative can be:
 mean / centroid (average of data
point)
 median / medoid (a point closer to the
mean)

6. Distance Function
 Euclidean Distance
 Manhatten Distance

7. Ex
:
 Find centroid and medoid of cluster containing three
two dimensional points (1,1) ,(2,3) and (6,2)
Centroid (mean)=
To find Kmedoid find the closest point
to mean
- For (1,1) = |3-1|+|2-1| = 3
- For (2,3)=|3-2|+|2-3| = 2
- - For (6,2)=|3-6|+|2-2|=3
K medoid = (2,3)
Closest point

8. Partitioning approach
 The grouping is done by minimizing
the sum of squares of distances
between data and the
corresponding cluster centroid.
 The quality of cluster Ci can be
measured by the within cluster
variation, which is the sum of
squared error between all objects in
Ci and the centroid ci, defined as

9. Main steps for K means

10. Example: Suppose we have 4 objects as your
training data point and each object have 2 tributes.
Each attribute represents coordinate of the
object
.
Y X OBJECT
1 1 A
1 2 B
3 4 C
4 5 D

11.  First step is to determine number of K.
K=2
 Initial centroids.
c1 = (1,1) and c2 = (2,1)

12. c2 = (2,1) c1 = (1,1)
= (1,1)
=1
= (1,1)
=0 min
= (2,1)
=0 min
= (2,1)
=1
= (4,3)
=2.83 min
= (4,3)
=3.61
= (5,4)
=4.24min
= (5,4)
=5
Calculate distance between objects and centroids.

13. New centroids
, )= c1 = (1,1)
𝒐𝒃𝒋 𝟏

14. Calculate distance between objects and new centroids
.
c2 = c1 = (1,1)
= (1,1)
=3.14
= (1,1)
=0 min
= (2,1)
=2.36
= (2,1)
=1 min
= (4,3)
=0.47min
= (4,3)
=3.61
= (5,4)
=1.89min
= (5,4)
=5

15. New centroids
𝒐𝒃𝒋𝟏𝒐𝒃𝒋𝟐
, )= , )=

16. Calculate distance between objects and new centroids
.
c2 = c1 = (,1)
= (1,1)
=4.3
= (1,1)
=0.5 min
= (2,1)
=3.54
= (2,1)
=0.5 min
= (4,3)
=0.71min
= (4,3)
=3.20
= (5,4)
=0.71min
= (5,4)
=4.61

17. New centroids
𝒐𝒃𝒋𝟏𝒐𝒃𝒋𝟐
, )= , )=
Centroids not changed then Stop

18. EX
:
 The following is a set of one-dimensional
points: {6; 12; 18; 24; 30; 42; 48}.
For each of the following set of initial centroids,
create two clusters by assigning each point to
the nearest centroid, and then calculate the
total squared error for each set of two clusters.
Show both the clusters and the total squared
error for each set of
centroid.
 {18; 45}.
 {15; 40}.

19. Sol
:
 First round of k means
- Cluster assign
42,48)
- Recompute mean
New centroid is the same as the previous
centroid
The final clusters are {6,12,18,24,30}
{42,48}

20. = ( + + + +) = 360
= ( + )= 18
Total square error is 360+18= 378

21. True or false
 K means is a hierarchical clustering
method.
 In k means clustering the number
of clusters produced is not known.
 A partition clustering is a division of
data objects into overlapping
clusters.
 K means results in optimal data
clustering.
 A centroid must be an actual data