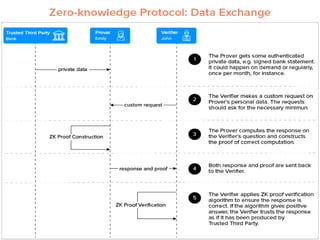
Zero-knowledge proof is an encryption method that allows one party to prove knowledge of a statement without revealing the information itself, introduced by MIT researchers in the 1980s. It requires interactive input from a verifier and has properties of completeness, soundness, and zero-knowledge. Current real-life applications of zero-knowledge proofs include platforms like Zcash and innovations by banks like ING, but adoption in blockchain is still slow due to various challenges.

1. BLOCKCHAIN TECHNOLOGY
Dr.P.Vishvapathi
Professor, CSE Department

2. I UNIT
ZERO KNOWLEDGE PROOF

3. • What is Zero Knowledge Proof?
• Zero-knowledge Proof is an encryption
scheme proposed by MIT researchers
Silvio Micali, Shafi Goldwasser, and Charles
Rackoff in the 1980s.
• In this method, one party (Prover) can prove
that a specific statement is true to the other
party (Verifier) without disclosing any
additional information.

4. • In cryptography, a zero-knowledge proof or zero-
knowledge protocol is a method by which one
party (the prover) can prove to another party (the
verifier) that they know a value x, without
conveying any information apart from the fact that
they know the value x.
• The essence of zero-knowledge proofs is that it is
trivial to prove that one possesses knowledge of
certain information by simply revealing it; the
challenge is to prove such possession without
revealing the information itself or any additional
information.

5. • If proving a statement requires that the prover possesses some
secret information, then the verifier will not be able to prove
the statement to anyone else without possessing the secret
information.
• The statement being proved must include the assertion that
the prover has such knowledge, but not the knowledge itself.
Otherwise, the statement would not be proved in zero-
knowledge because it provides the verifier with additional
information about the statement by the end of the protocol.
• A zero-knowledge proof of knowledge is a special case when
the statement consists only of the fact that the prover
possesses the secret information.Interactive zero-knowledge
proofs require interaction between the individual (or computer
system) proving their knowledge and the individual validating
the proof.

6. A protocol implementing zero-knowledge proofs of
knowledge must necessarily require interactive input
from the verifier.
This interactive input is usually in the form of one or
more challenges such that the responses from the
prover will convince the verifier if and only if the
statement is true, i.e., if the prover does possess the
claimed knowledge. If this were not the case, the
verifier could record the execution of the protocol and
replay it to convince someone else that they possess
the secret information.
The new party's acceptance is either justified since the
replayer does possess the information (which implies
that the protocol leaked information, and thus, is not
proved in zero-knowledge), or the acceptance is
spurious, i.e., was accepted from someone who does
not actually possess the information.

7. The Ali Baba cave
There is a well-known story presenting the fundamental
ideas of zero-knowledge proofs, first published by
Jean-Jacques Quisquater and others in their paper "How to
Explain Zero-Knowledge Protocols to Your Children".It is
common practice to label the two parties in a zero-
knowledge proof as Peggy (the prover of the statement)
and Victor (the verifier of the statement).
In this story, Peggy has uncovered the secret word used to
open a magic door in a cave. The cave is shaped like a
ring, with the entrance on one side and the magic door
blocking the opposite side. Victor wants to know whether
Peggy knows the secret word; but Peggy, being a very
private person, does not want to reveal her knowledge (the
secret word) to Victor or to reveal the fact of her knowledge
to the world in general.

11. ALI BABA CAVE

12. • They label the left and right paths from the entrance A and B. First, Victor
waits outside the cave as Peggy goes in. Peggy takes either path A or B;
Victor is not allowed to see which path she takes. Then, Victor enters the
cave and shouts the name of the path he wants her to use to return,
either A or B, chosen at random. Providing she really does know the magic
word, this is easy: she opens the door, if necessary, and returns along the
desired path.
• However, suppose she did not know the word. Then, she would only be
able to return by the named path if Victor were to give the name of the
same path by which she had entered. Since Victor would choose A or B at
random, she would have a 50% chance of guessing correctly. If they were
to repeat this trick many times, say 20 times in a row, her chance of
successfully anticipating all of Victor's requests would become vanishingly
small (about one in a million).
• Thus, if Peggy repeatedly appears at the exit Victor names, he can
conclude that it is extremely probable that Peggy does, in fact, know the
secret word.

13. • One side note with respect to third-party observers: even if Victor is
wearing a hidden camera that records the whole transaction, the only
thing the camera will record is in one case Victor shouting "A!" and
Peggy appearing at A or in the other case Victor shouting "B!" and
Peggy appearing at B.
• A recording of this type would be trivial for any two people to fake
(requiring only that Peggy and Victor agree beforehand on the
sequence of A's and B's that Victor will shout). Such a recording will
certainly never be convincing to anyone but the original participants.
• In fact, even a person who was present as an observer at the original
experiment would be unconvinced, since Victor and Peggy might have
orchestrated the whole "experiment" from start to finish.

14. • Notice that Peggy could prove to Victor that she knows the magic word, without revealing it to him, in a single trial. If both Victor and Peggy go
together to the mouth of the cave, Victor can watch Peggy go in through A and come out through B.
• This would prove with certainty that Peggy knows the magic word, without revealing the magic word to Victor. However, such a proof could be
observed by a third party, or recorded by Victor and such a proof would be convincing to anybody.
• In other words, Peggy could not refute such proof by claiming she colluded with Victor, and she is therefore no longer in control of who is aware
of her knowledge.

15. • A zero-knowledge proof must satisfy three properties:
• Completeness: if the statement is true, the honest verifier (that is,
one following the protocol properly) will be convinced of this fact by
an honest prover.
• Soundness: if the statement is false, no cheating prover can convince
the honest verifier that it is true, except with some small probability.
• Zero-knowledge: if the statement is true, no verifier learns anything
other than the fact that the statement is true. In other words, just
knowing the statement (not the secret) is sufficient to imagine a
scenario showing that the prover knows the secret. This is formalized
by showing that every verifier has some simulator that, given only
the statement to be proved (and no access to the prover), can
produce a transcript that "looks like" an interaction between the
honest prover and the verifier in question.
• The first two of these are properties of more general
interactive proof systems. The third is what makes the proof zero-
knowledge.

16. Zero-knowledge proofs are not proofs in the mathematical sense of
the term because there is some small probability, the soundness
error, that a cheating prover will be able to convince the verifier of a
false statement.
In other words, zero-knowledge proofs are probabilistic "proofs"
rather than deterministic proofs. However, there are techniques to
decrease the soundness error to negligibly small values.

18. • Real-Life Examples of Convergence of Zero Knowledge Proofs and
Blockchain
• 1. Zcash: ZCash is an open-source and permissionless blockchain
platform that offers the functionality to keep transactions
‘transparent’ and ‘shielded’ as per the requirement.
• In the former case, the transactions are governed by a t-addr, just
like bitcoin transactions. While in the latter case, a zero-knowledge
proof called zk-SNARKs is used and the transactions are controlled
by a z-addr.
• 2. ING : ING is a Netherlands based bank that has introduced its
own zero-knowledge blockchain. However, they have modified
their zero-knowledge system to make it a zero-knowledge
knowledge range proof to lower down the need for computational
power.
• This way, they have prepared their zero-knowledge system to
elevate the impact of blockchain in fintech.

19. • 3. ZCoin
• The company uses Zerocoin protocol, which is based
on zero-knowledge proof, to enhance security and
anonymity in the transaction process. However, what
makes it distinct from other projects working on this
concept is that it offers scalability too.
• Though various international actors have started
showing an interest in implementing the concept of
zero-knowledge proof into the blockchain, the
adoption pace is too slow. And the prime reason
behind is the following set of challenges associated
with the addition of ZKP into the blockchain
environment.