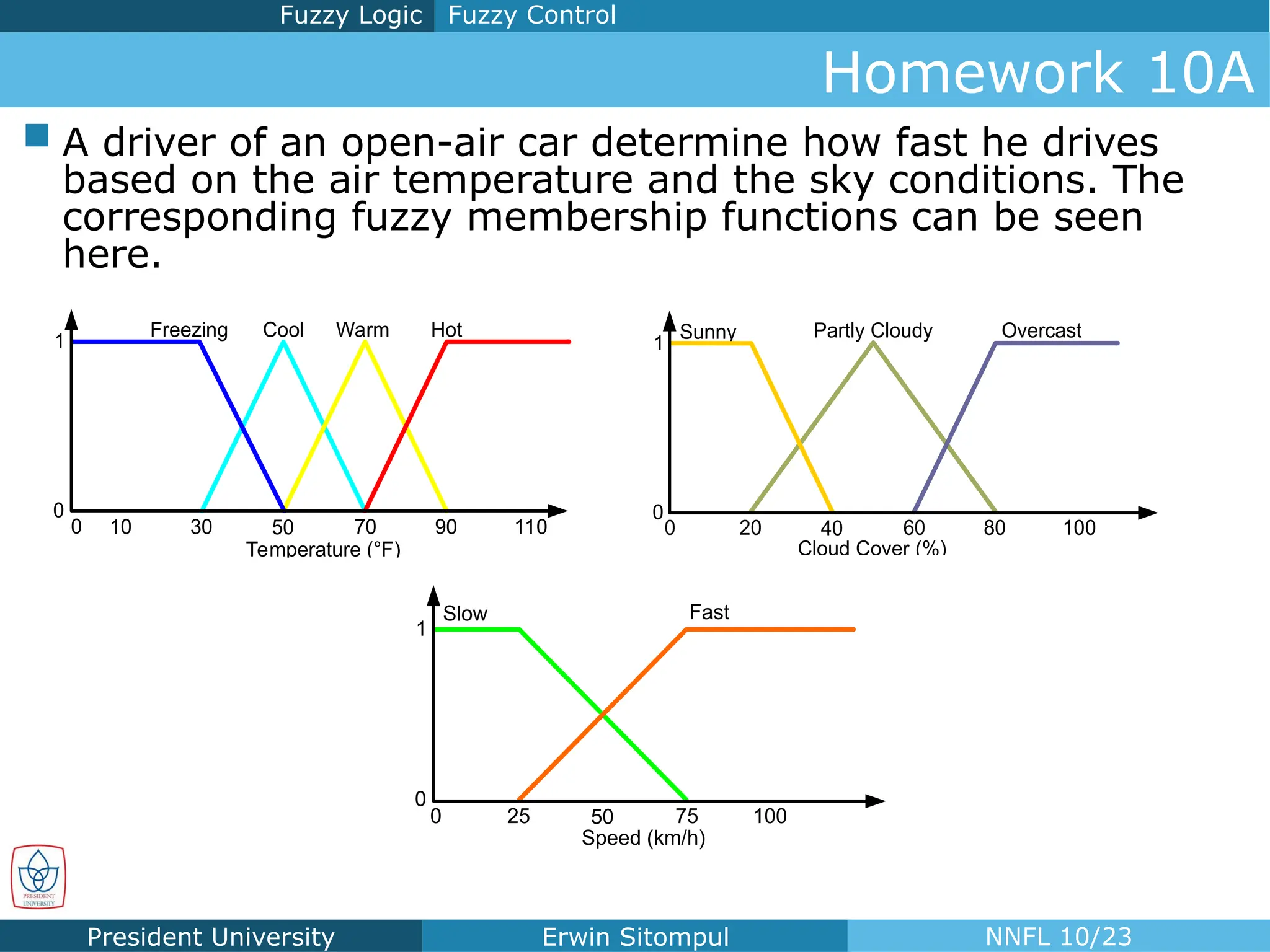
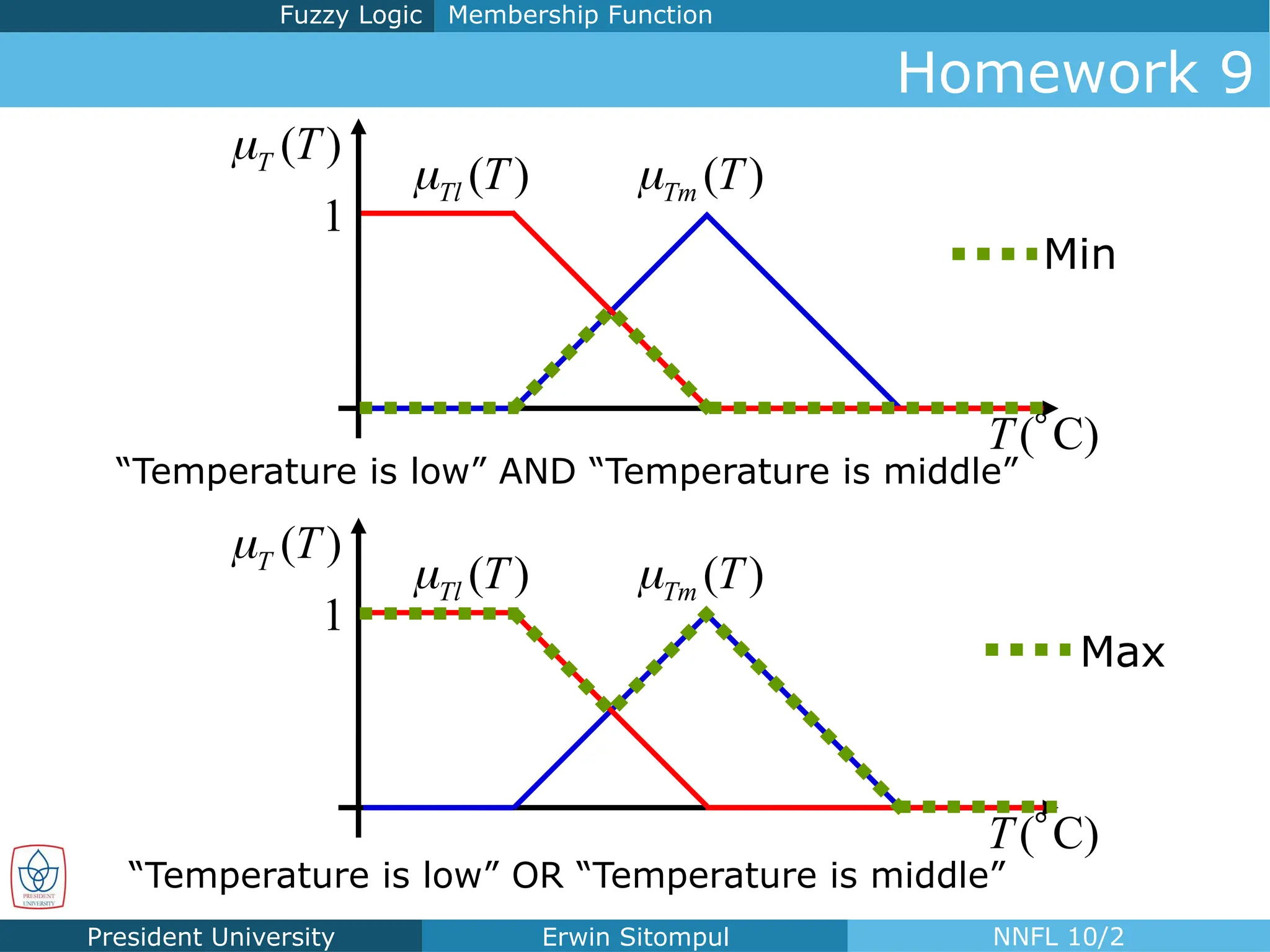
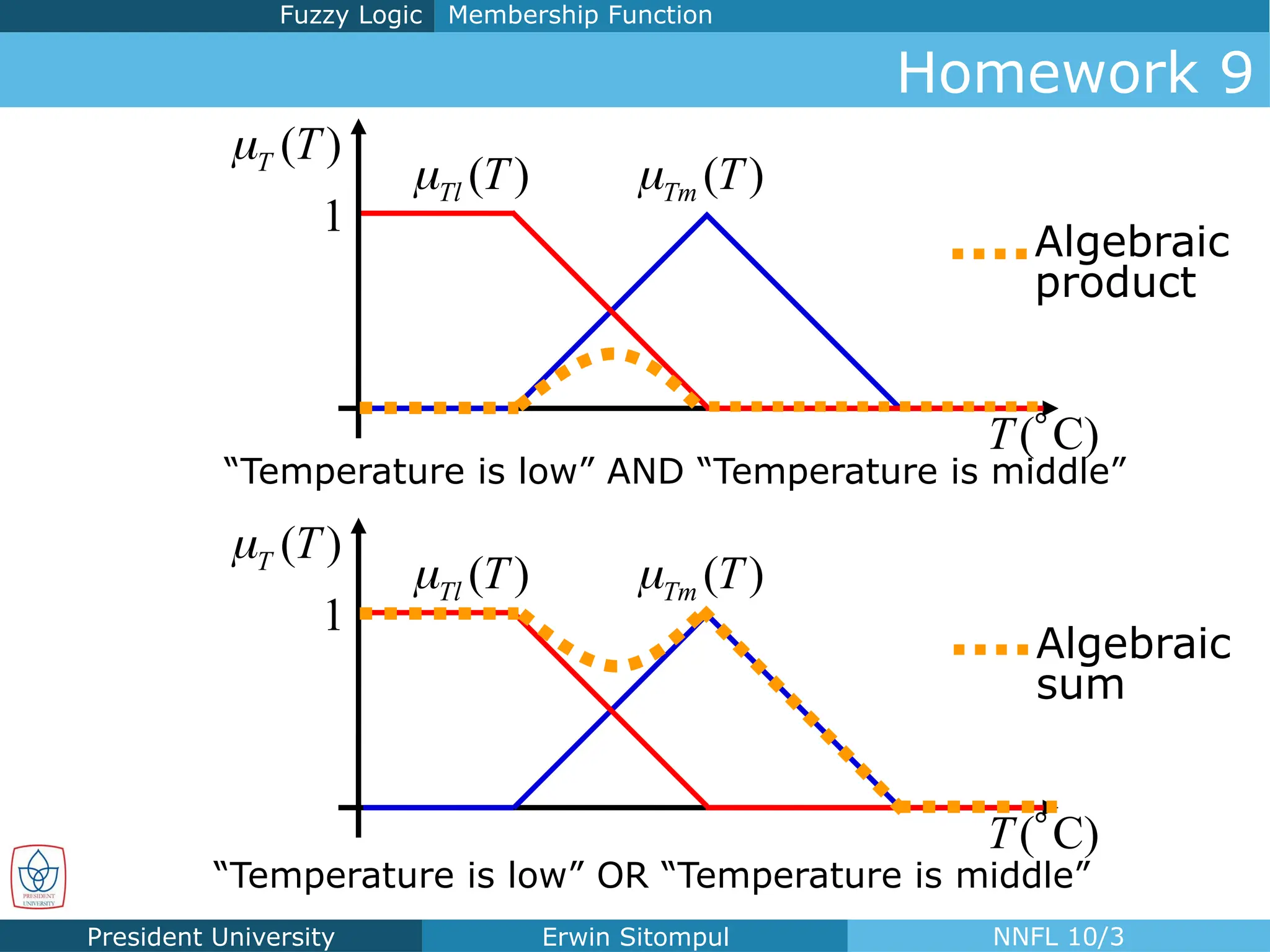
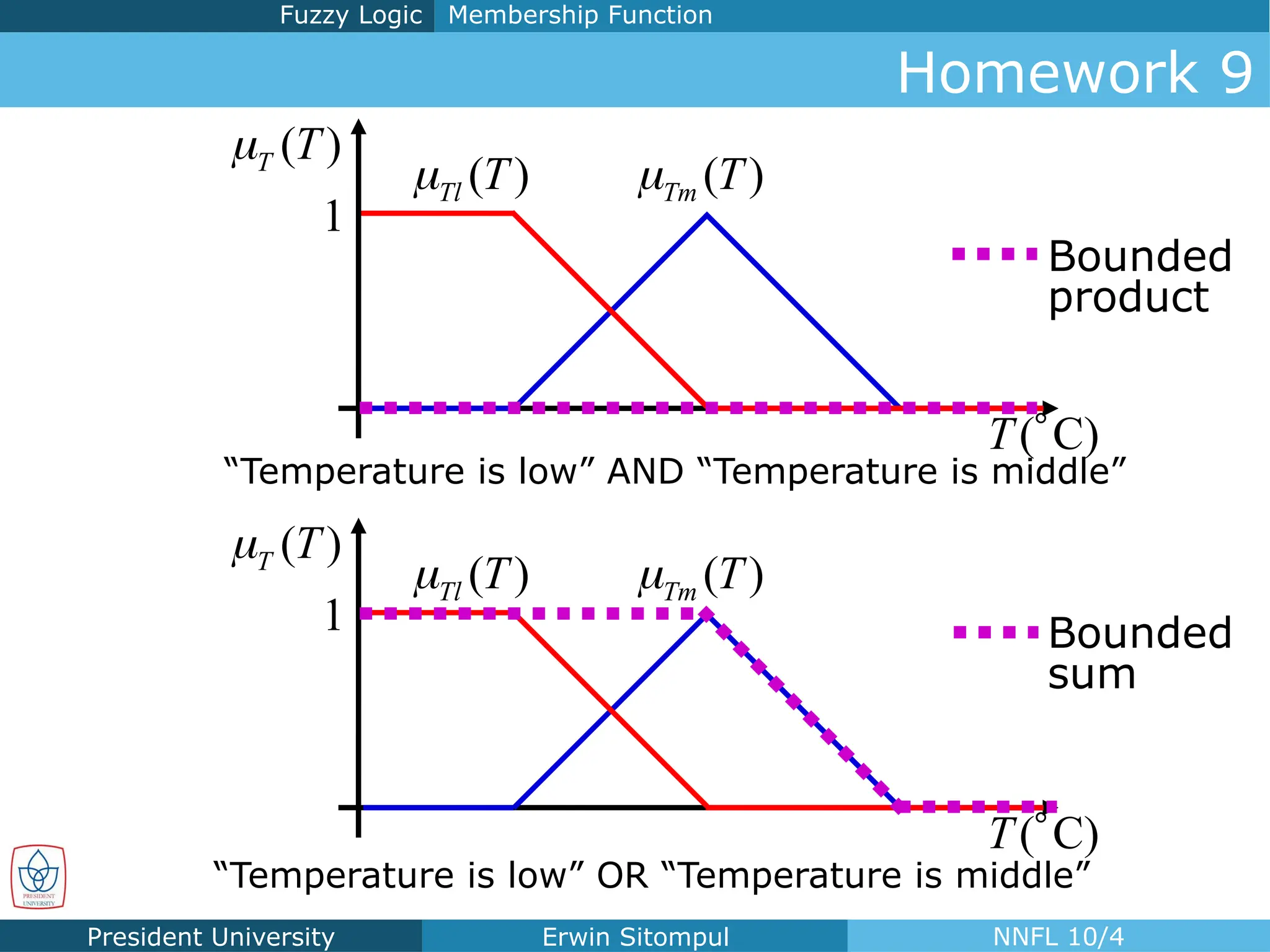
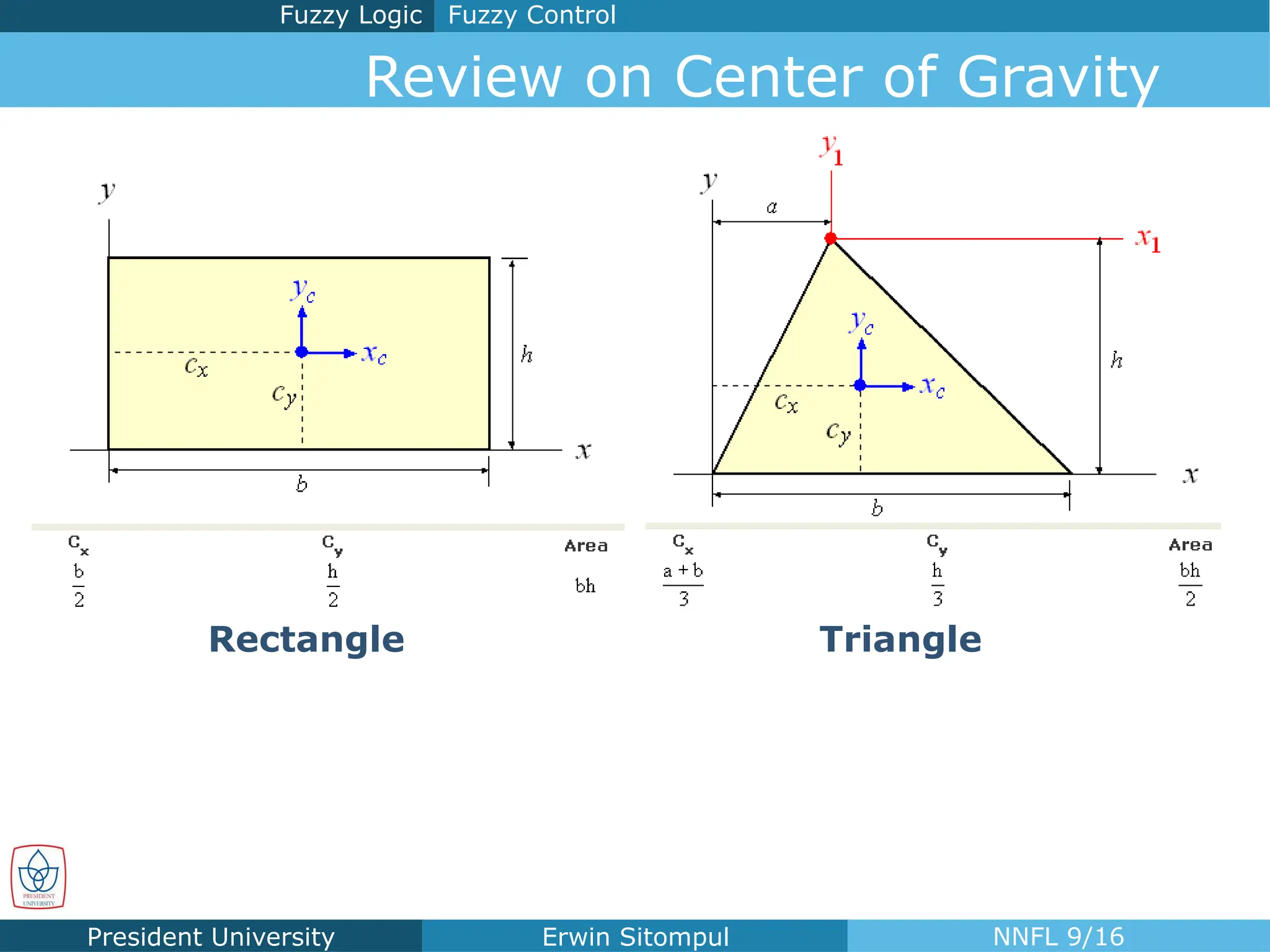
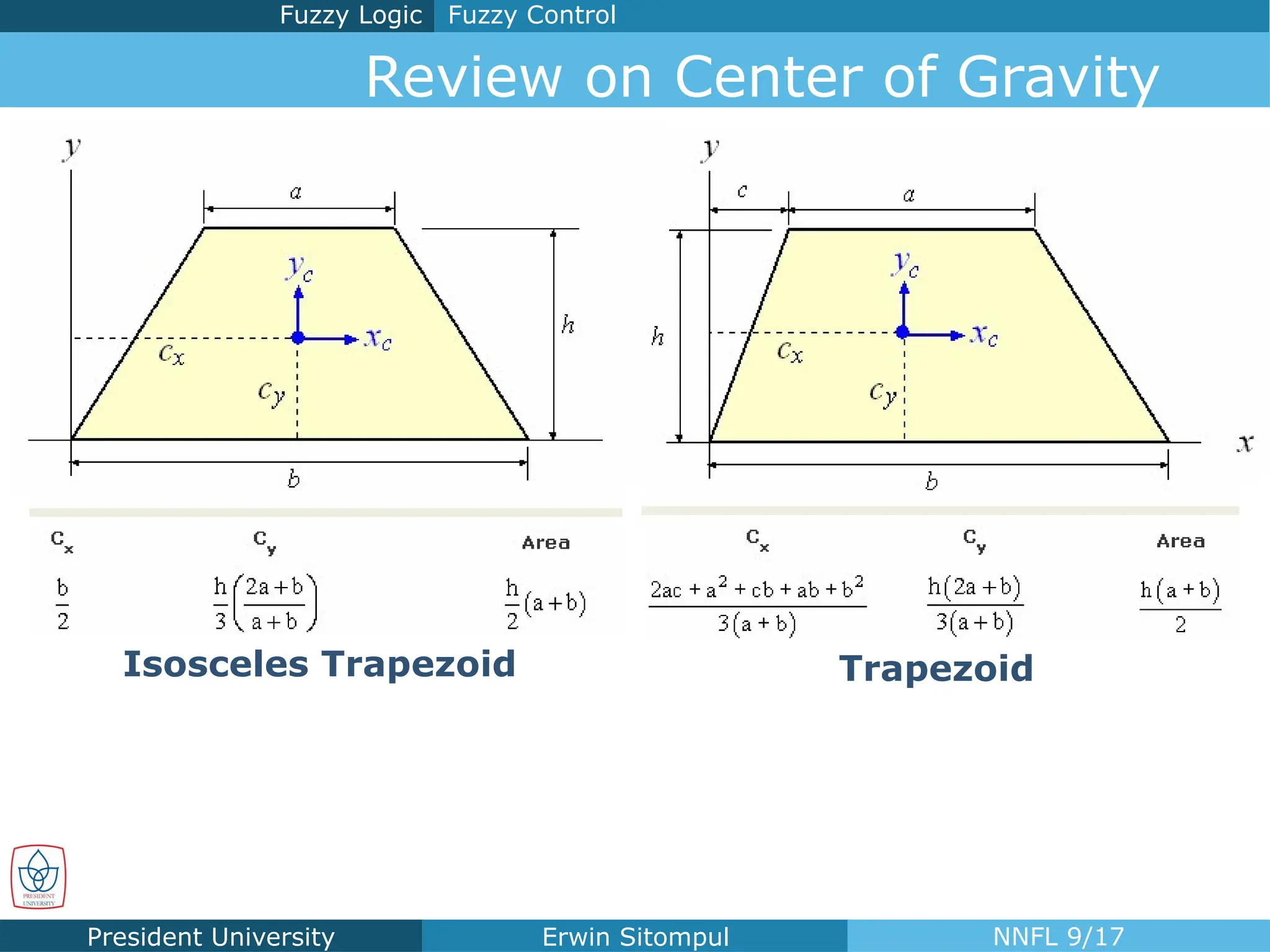
The document discusses the introduction to neural networks and fuzzy logic, focusing on fuzzy control and its operations, such as fuzzification, inference, and defuzzification. It outlines the definitions and applications of fuzzy membership functions, fuzzy rules, and various operators for creating a fuzzy control system. Additionally, it includes examples and homework assignments related to driving scenarios that utilize fuzzy logic principles.

1. Lecture 10
Introduction to Neural Networks
and Fuzzy Logic
President University Erwin Sitompul NNFL 10/1
Dr.-Ing. Erwin Sitompul
President University
http://zitompul.wordpress.com
2 0 1 8

2. President University Erwin Sitompul NNFL 10/2
( )
T T

( )
Tl T
 ( )
Tm T

( C)
T 
1
“Temperature is low” AND “Temperature is middle”
( )
T T

( )
Tl T
 ( )
Tm T

( C)
T 
1
“Temperature is low” OR “Temperature is middle”
Min
Max
Membership Function
Fuzzy Logic
Homework 9

3. President University Erwin Sitompul NNFL 10/3
( )
T T

( )
Tl T
 ( )
Tm T

( C)
T 
1
“Temperature is low” AND “Temperature is middle”
( )
T T

( )
Tl T
 ( )
Tm T

( C)
T 
1
“Temperature is low” OR “Temperature is middle”
Algebraic
product
Algebraic
sum
Homework 9
Membership Function
Fuzzy Logic

4. President University Erwin Sitompul NNFL 10/4
( )
T T

( )
Tl T
 ( )
Tm T

( C)
T 
1
“Temperature is low” AND “Temperature is middle”
( )
T T

( )
Tl T
 ( )
Tm T

( C)
T 
1
“Temperature is low” OR “Temperature is middle”
Bounded
product
Bounded
sum
Homework 9
Membership Function
Fuzzy Logic

5. President University Erwin Sitompul NNFL 10/5
Further Fuzzy Set Operations
2
1/ 2
3
( ) ( )
( ) ( )
( ) ( )
very A A
morl A A
extremely A A
x x
x x
x x
 
 
 



1/3
( ) 1 ( )
( ) ( )
not A A
slightly A A
x x
x x
 
 
 

Fuzzy Control
Fuzzy Logic
Dilation
Concentration

6. President University Erwin Sitompul NNFL 10/6
Fuzzy Control Loop
Fuzzy Control
Fuzzy Logic

7. President University Erwin Sitompul NNFL 9/7
 Prior to fuzzy control, the followings must be defined:
 Fuzzy membership functions
 Fuzzy logic operators
 Fuzzy rules, including fuzzy linguistic value and
linguistic variable
 The processing steps in a fuzzy control include:
 Fuzzification
 Implication / Inference Core
 Accumulation
 Defuzzification
Fuzzy Control
Fuzzy Logic
Fuzzy Inference

8. President University Erwin Sitompul NNFL 10/8
Fuzzy Control
Fuzzy Logic
Fuzzy Rules
 Example of a fuzzy rule while “Driving a Car”:
“IF the distance to the car in front is small, AND
the distance is decreasing slowly, THEN
decelerate quite big”
 The question that arises:
Given a certain distance and a certain change of
distance, what (crisp) value of acceleration should
we select?

9. President University Erwin Sitompul NNFL 10/9
Definition of Fuzzy Membership Functions
v. small
Distance
small perfect big v. big moderate
Distance decrease
slow fast very fast
v. slow
Acceleration
–small zero+small +big
–big
Fuzzy Control
Fuzzy Logic

10. President University Erwin Sitompul NNFL 10/10
Fuzzification
Observation/
measurement
Observation/
measurement
• Distance between
small and perfect
• Distance decrease can
be moderate or fast
• What acceleration
should be applied?
Fuzzy Control
Fuzzy Logic
v. small
Distance
small perfect big v. big moderate
Distance decrease
slow fast very fast
v. slow
Acceleration
–small zero+small +big
–big
10 m 4m s

11. President University Erwin Sitompul NNFL 9/11
RULE 1:
IF distance is small
THEN decelerate small
0.55
Inference core: Clipping
Clip the fuzzy membership
function of “–small” at the height
given by the premises (0.55).
Later, the clipped area will be
considered in the final decision
Implication of Rules
Fuzzy Control
Fuzzy Logic
v. small
Distance
small perfect big v. big
Observation/
measurement
Acceleration
–small zero +small +big
–big
10 m

12. President University Erwin Sitompul NNFL 9/12
RULE 2:
IF distance decrease is
moderate THEN keep
the speed
Inference core: Clipping
Clip the fuzzy membership
function of “zero” at the height
given by the premises (0.7).
Later, the clipped area will be
considered in the final decision
Implication of Rules
Fuzzy Control
Fuzzy Logic
Observation/
measurement
Acceleration
–small zero+small +big
–big
moderate
Distance decrease
slow fast very fast
v. slow
0.7
4m s

13. President University Erwin Sitompul NNFL 10/13
 From each rule, a clipped area is obtained. But, in the
end only one single output is wanted. How do we make
a final decision?
–small zero+small +big
–big
Acceleration
Accumulation
Rule 1
Rule 2
Fuzzy Control
Fuzzy Logic
 In the accumulation (aggregation) step, all clipped
areas are merged into one merged area (taking the
union).
 Rules with high premises will contribute large clipped
area to the merged area. These rules will “pull” that
merged area towards their own central value.

14. President University Erwin Sitompul NNFL 9/14
–small zero+small +big
–big
Acceleration
 In this last step, the returned value is the wanted
acceleration.
 Out of many possible ways, the center of gravity is the
commonly used method in defuzzification.
Crisp value
2
. . 2.3m s
i e 
Center of gravity
Fuzzy Control
Fuzzy Logic
Defuzzification

15. President University Erwin Sitompul NNFL 10/15
0.55
acceleration
1. Clipping approach:
0.55
acceleration
2. Scaling approach:
   
Impl , ( ) min , ( )
A B A B
y y
   

A

( )
B y

Fuzzification value Membership function
 
Impl , ( ) ( )
A B A B
y y
   
 
A

( )
B y

Min-Operator
Algebraic Product
Fuzzy Control
Fuzzy Logic
Inference Core
 There are two approaches that can be used for
inference core:

16. President University Erwin Sitompul NNFL 9/16
Rectangle Triangle
Fuzzy Control
Fuzzy Logic
Review on Center of Gravity

17. President University Erwin Sitompul NNFL 9/17
Isosceles Trapezoid Trapezoid
Fuzzy Control
Fuzzy Logic
Review on Center of Gravity

18. President University Erwin Sitompul NNFL 10/18
Summary of Fuzzy Control
Fuzzy Control
Fuzzy Logic
1. Fuzzify inputs, determine the degree of membership
for all terms in the premise.
2. Apply fuzzy logic operators, if there are multiple
terms in the premise (min-max, algebraic, bounded).
3. Apply inference core (clipping, scaling, etc.)
4. Accumulate all outputs (union operation i.e. max,
sum, etc.)
5. Defuzzify (center of gravity of the merged outputs,
max-method, modified center of gravity, height
method, etc)

19. President University Erwin Sitompul NNFL 10/19
Limitations of Fuzzy Control
Fuzzy Control
Fuzzy Logic
 Definition and fine-tuning of membership functions
need experience (covered range, number of MFs,
shape).
 Defuzzification may produce undesired results (needs
redefinition of membership functions).

20. President University Erwin Sitompul NNFL 10/20
Homework 10
v. small
Distance to next car [m]
small perfect big v. big
0 5 10 15 20 25
1
Speed change [m/s2
]
constant growing
declining
–small zero +small +big
–big
Acceleration adj. [m/s2
]
–2 –1 0 1 2
1
–10 –5 0 5 10
1
Fuzzy Control
Fuzzy Logic
 A fuzzy controller is to be used in driving a car. The
fuzzy membership functions for the two inputs and one
output are defined as below.

21. President University Erwin Sitompul NNFL 10/21
Homework 10 (Cont.)
Fuzzy Control
Fuzzy Logic
 A fuzzy controller is to be used in driving a car. The
fuzzy rules are given as follows.
Rule 1: IF distance is small AND speed is declining,
THEN maintain acceleration.
Rule 2: IF distance is small AND speed is constant,
THEN acceleration adjustment negative small.
Rule 3: IF distance is perfect AND speed is declining,
THEN acceleration adjustment positive
small.
Rule 4: IF distance is perfect AND speed is constant,
THEN maintain acceleration.

22. President University Erwin Sitompul NNFL 10/22
Homework 10 (Cont.)
Fuzzy Control
Fuzzy Logic
 Using Min-Max as fuzzy operators, clipping as
inference core, union operator as accumulator, and
center of gravity method as defuzzifier, find the
output of the controller if the measurements confirms
that distance to next car is 13 m and the speed is
increasing by 2.5 m/s2
.

23. President University Erwin Sitompul NNFL 10/23
Homework 10A
Fuzzy Control
Fuzzy Logic
 A driver of an open-air car determine how fast he drives
based on the air temperature and the sky conditions. The
corresponding fuzzy membership functions can be seen
here.
50 70 90 110
30
10
Temperature (°F)
Freezing Cool Warm Hot
0
1
0 40 60 80 100
20
0
Cloud Cover (%)
Overcast
Partly Cloudy
Sunny
0
1
50 75 100
25
0
Speed (km/h)
Slow Fast
0
1

24. President University Erwin Sitompul NNFL 10/24
Homework 10A (Cont.)
Fuzzy Control
Fuzzy Logic
 After years of experience, he summarizes his personal
driving rules as follows:
Rule 1: IF it is sunny AND warm, THEN drive fast.
Rule 2: IF it is partly cloudy AND hot, THEN drive slow.
Rule 3: IF it is partly cloudy, THEN drive fast.
 You are now assigned to design a fuzzy control with the
following requirements:
 Fuzzy logic operators: algebraic sum / product
 Inference core: scaling
 Accumulator: union operator
 Defuzzification: center of gravity method
 The speed limit is 120 km/h. How fast will the driver go if in
one day the temperature is 65 °F and the cloud cover is
25 %?
 Deadline: Sunday, 25 March 2018.