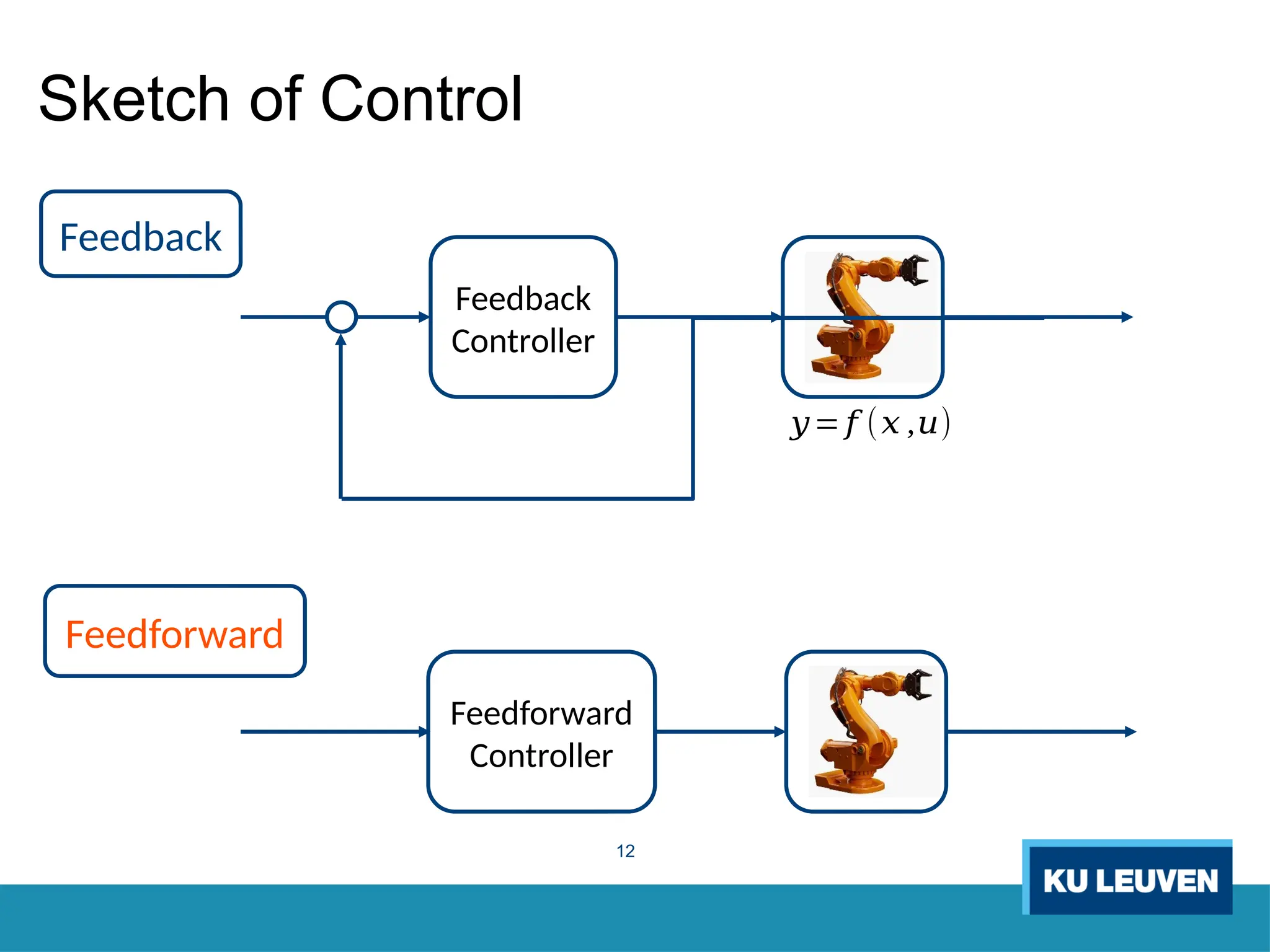
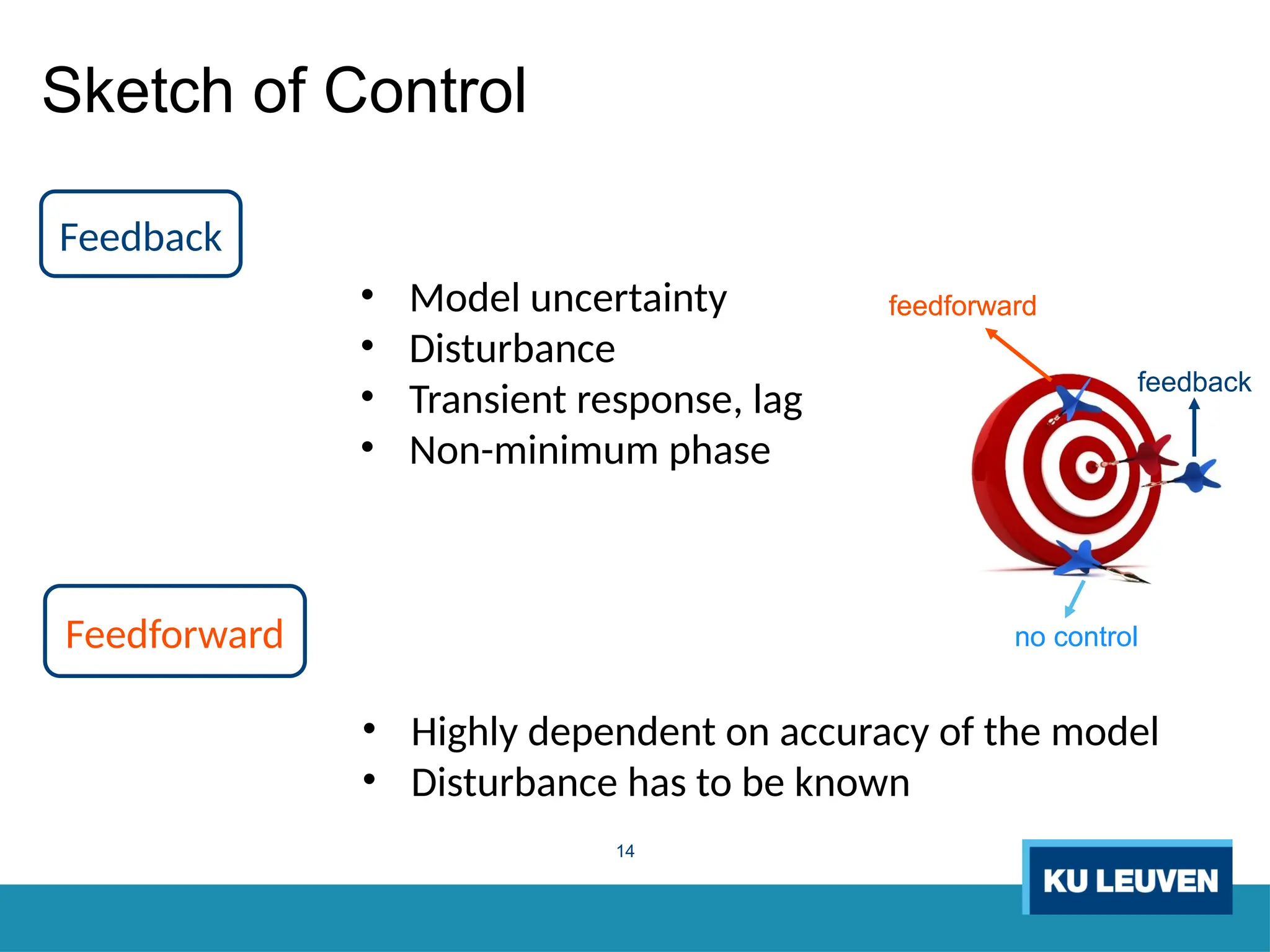
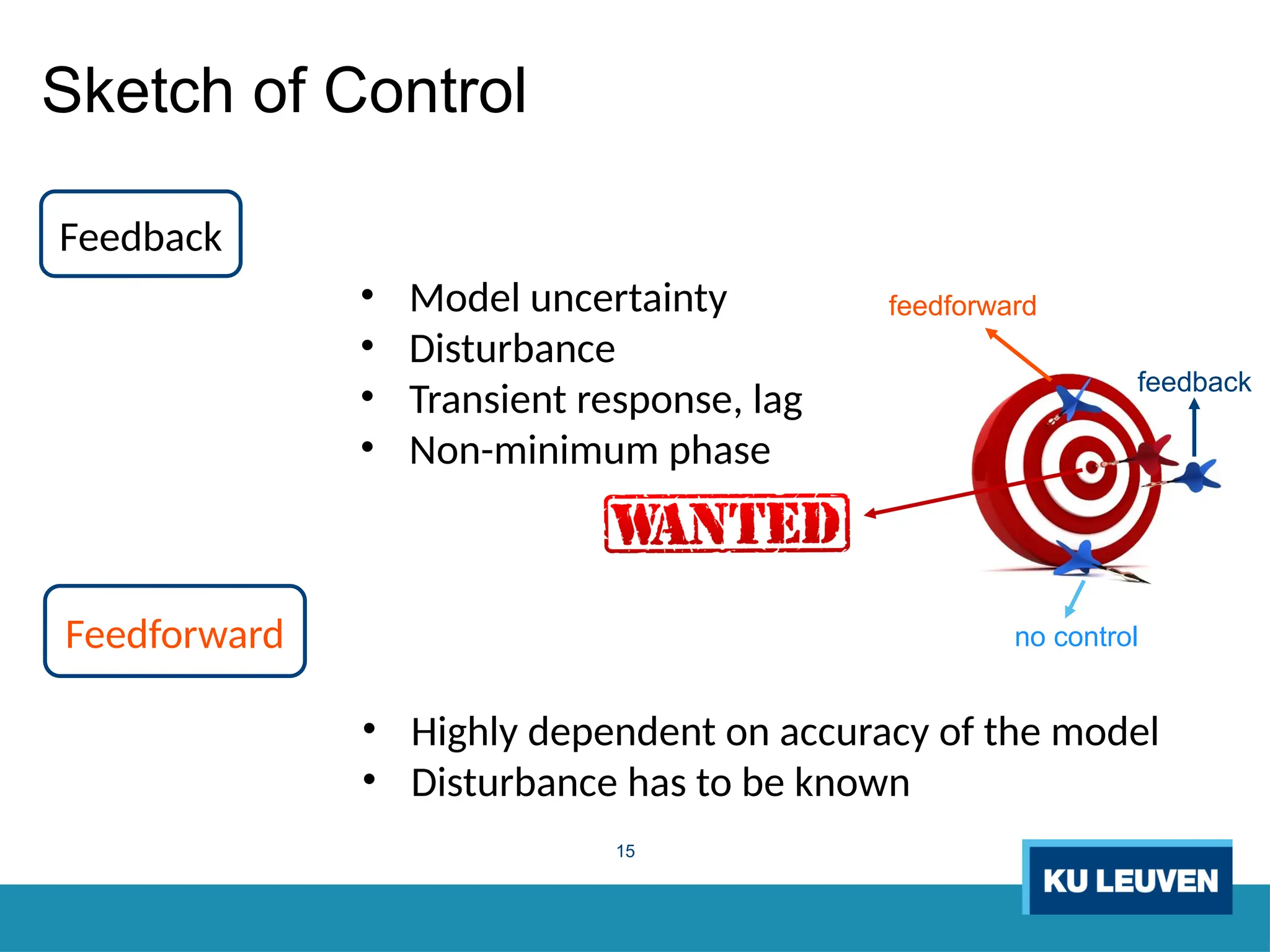
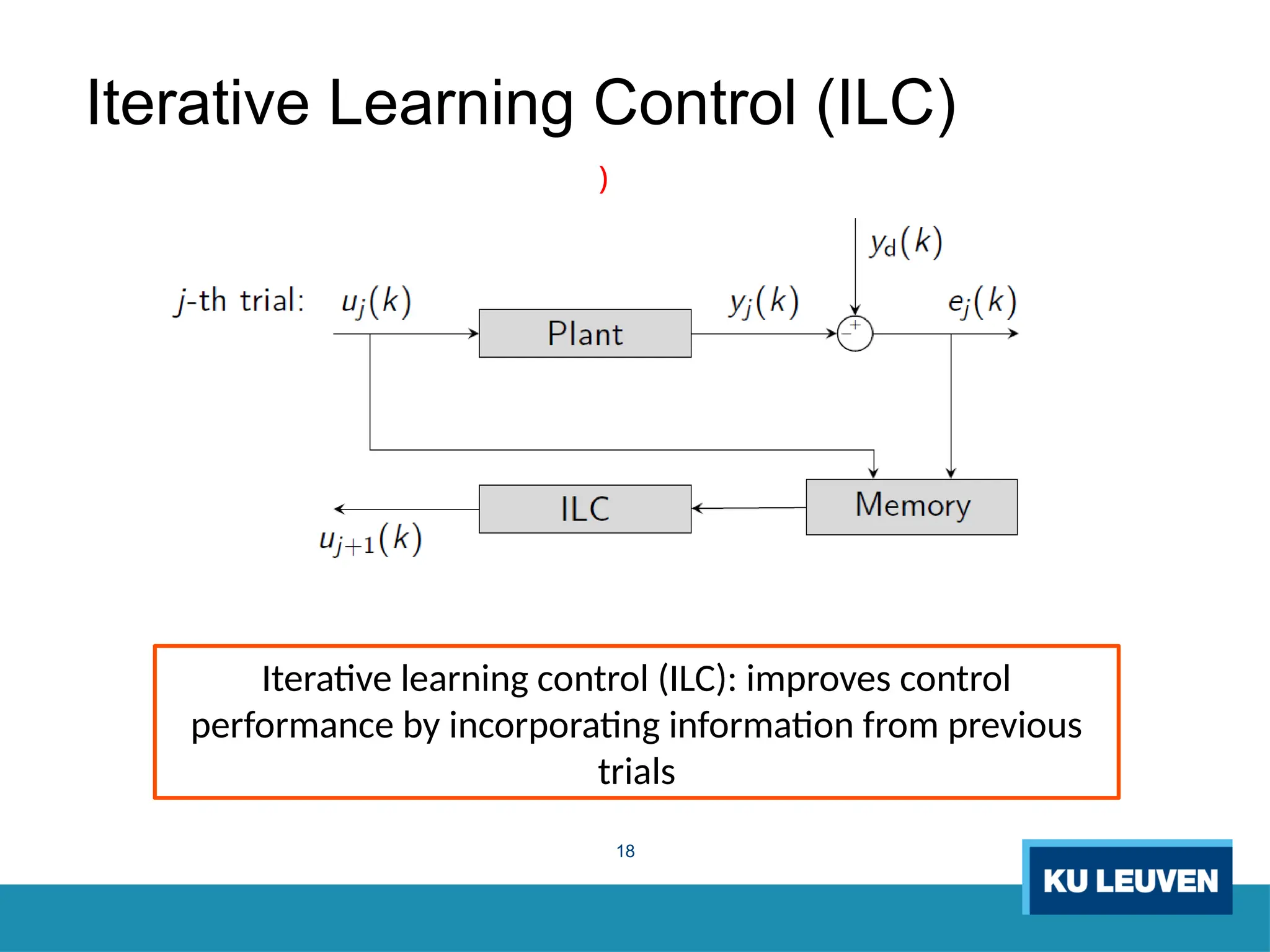
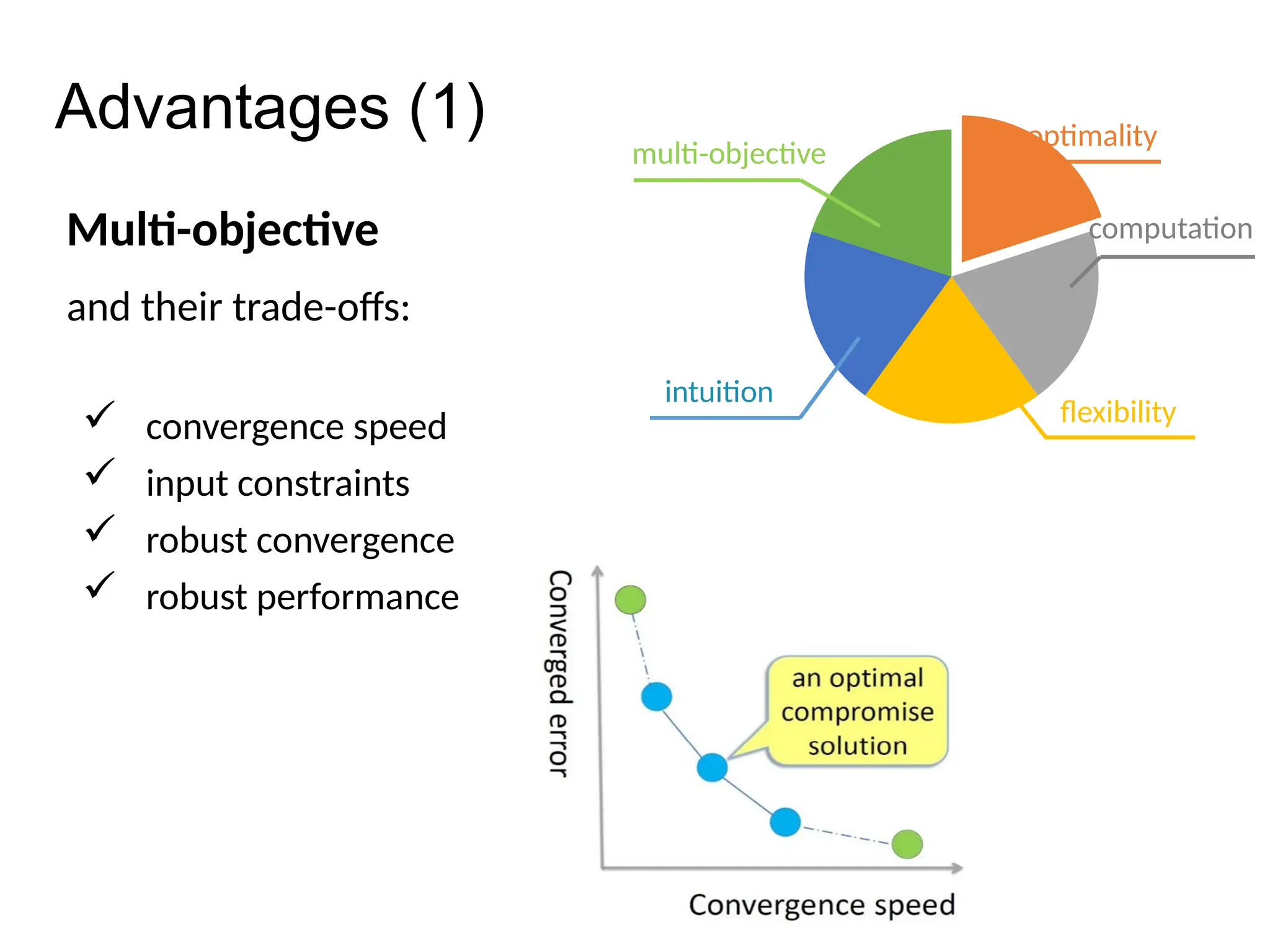
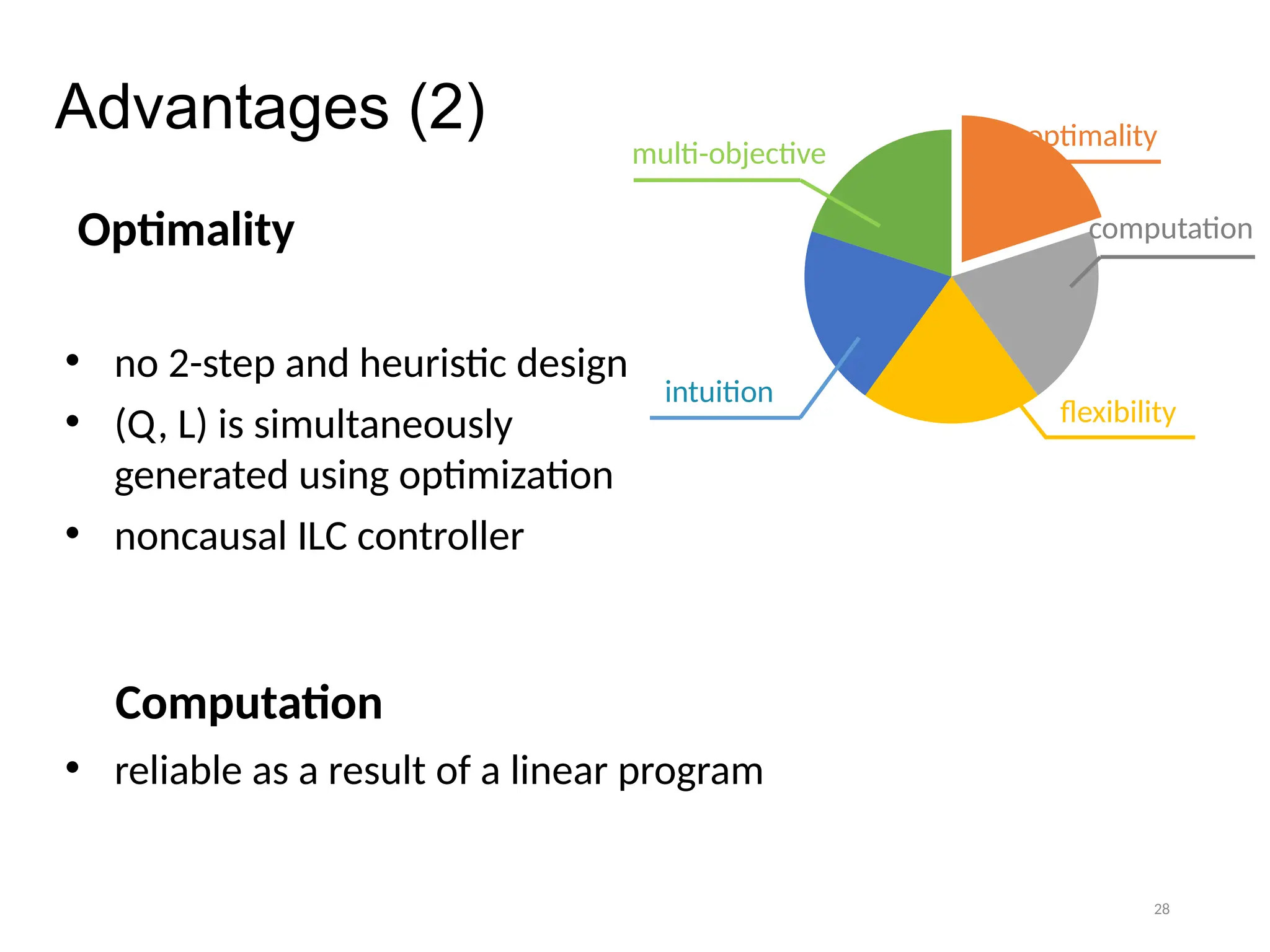
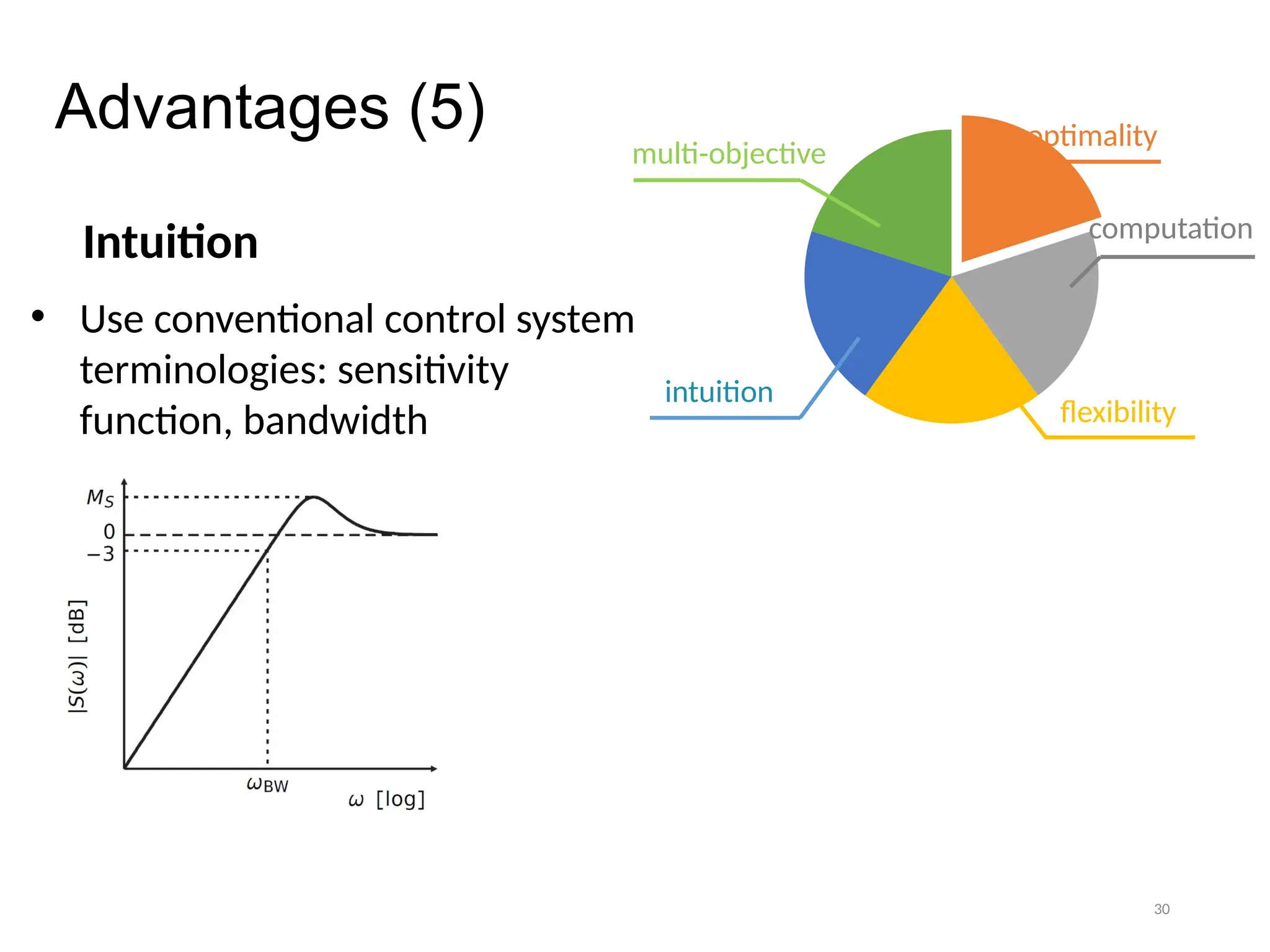
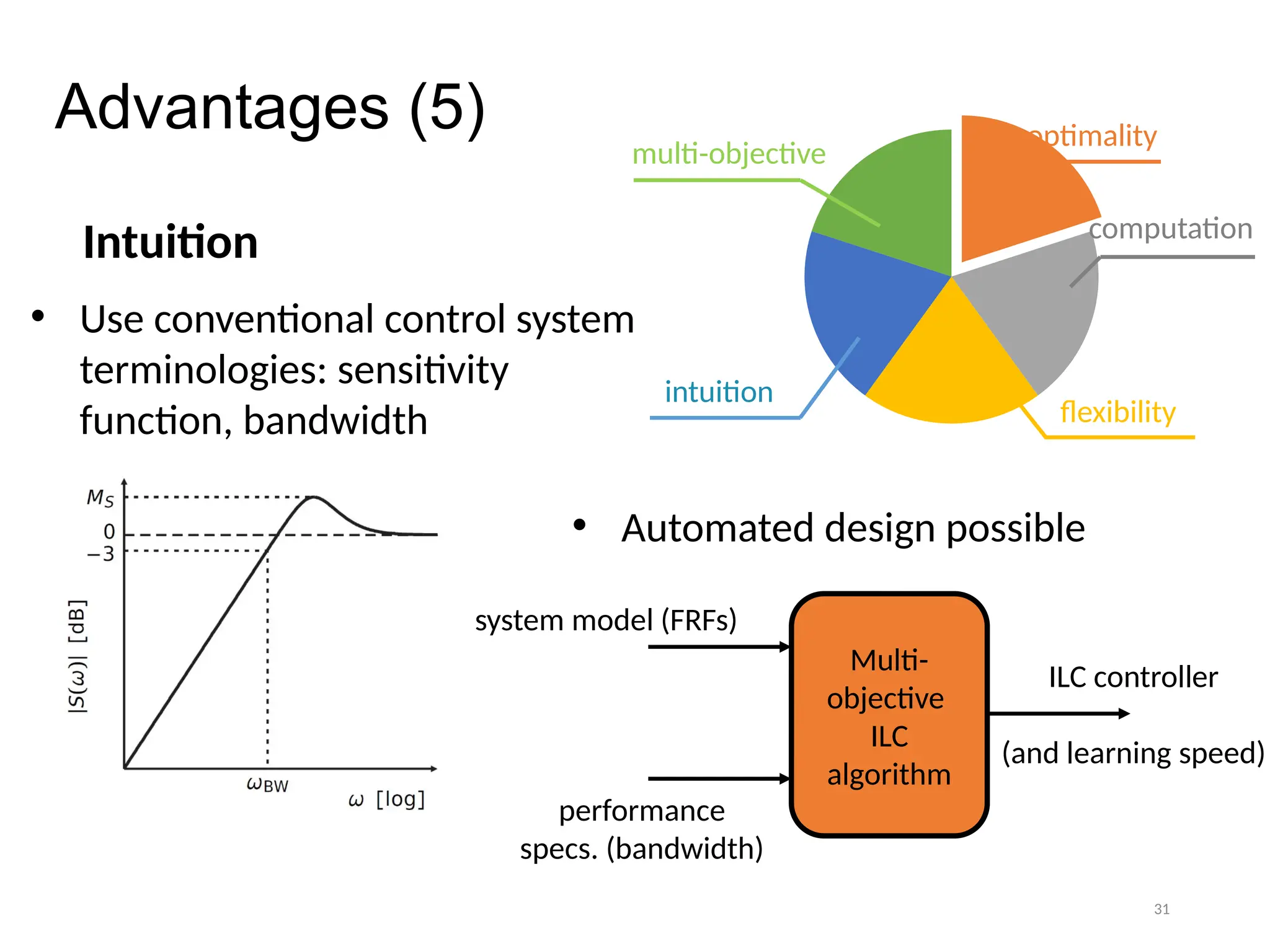
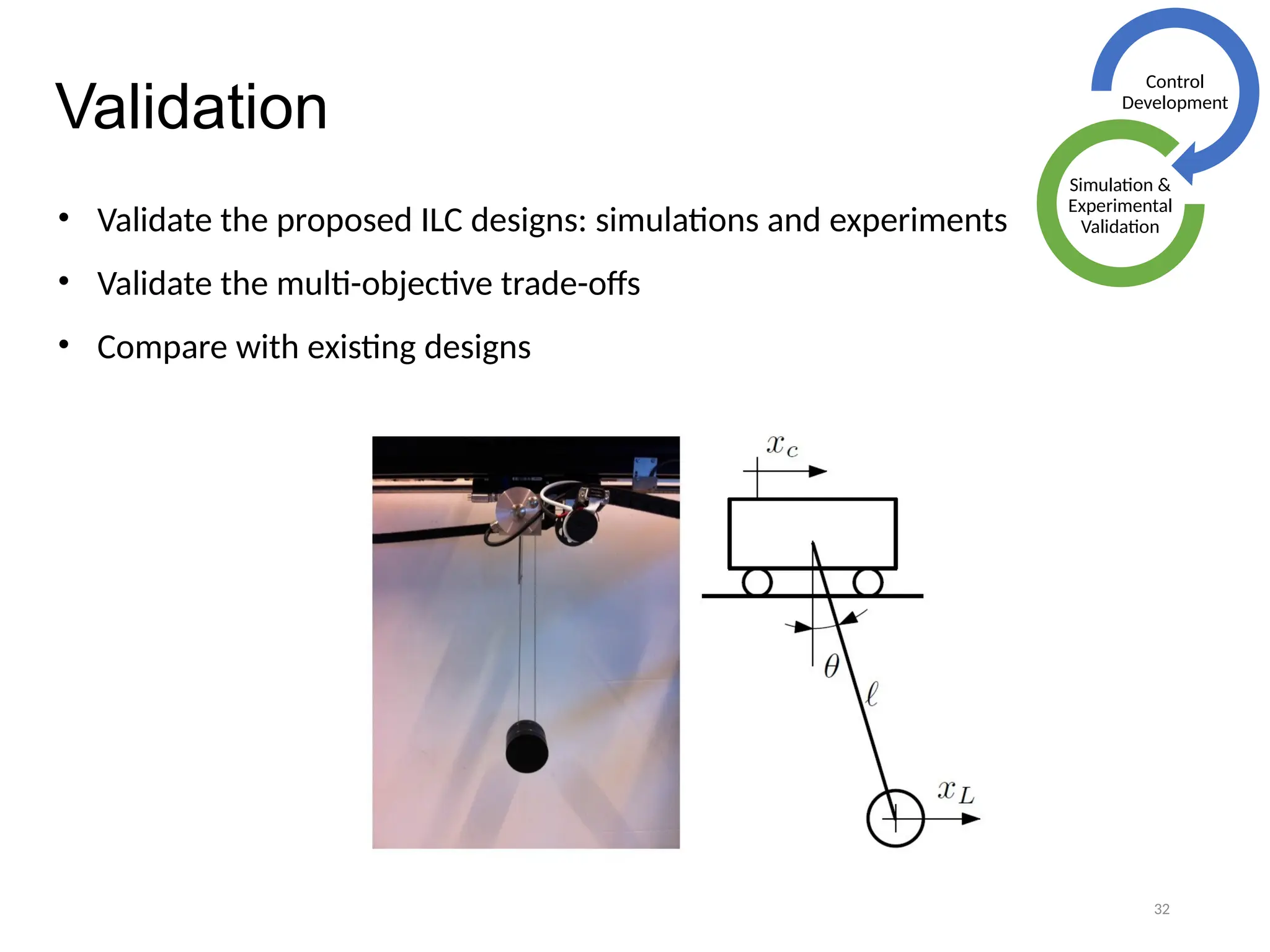
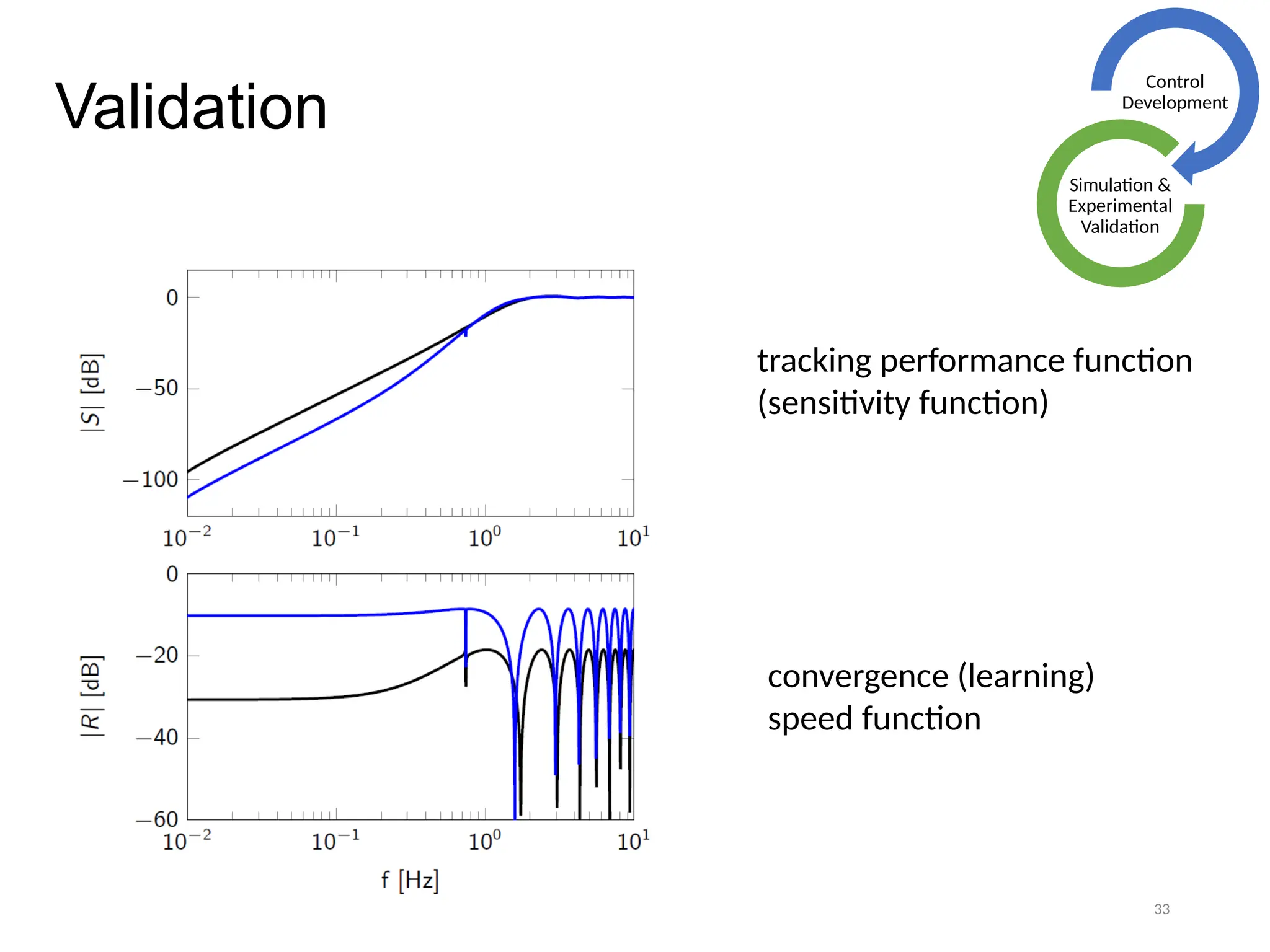
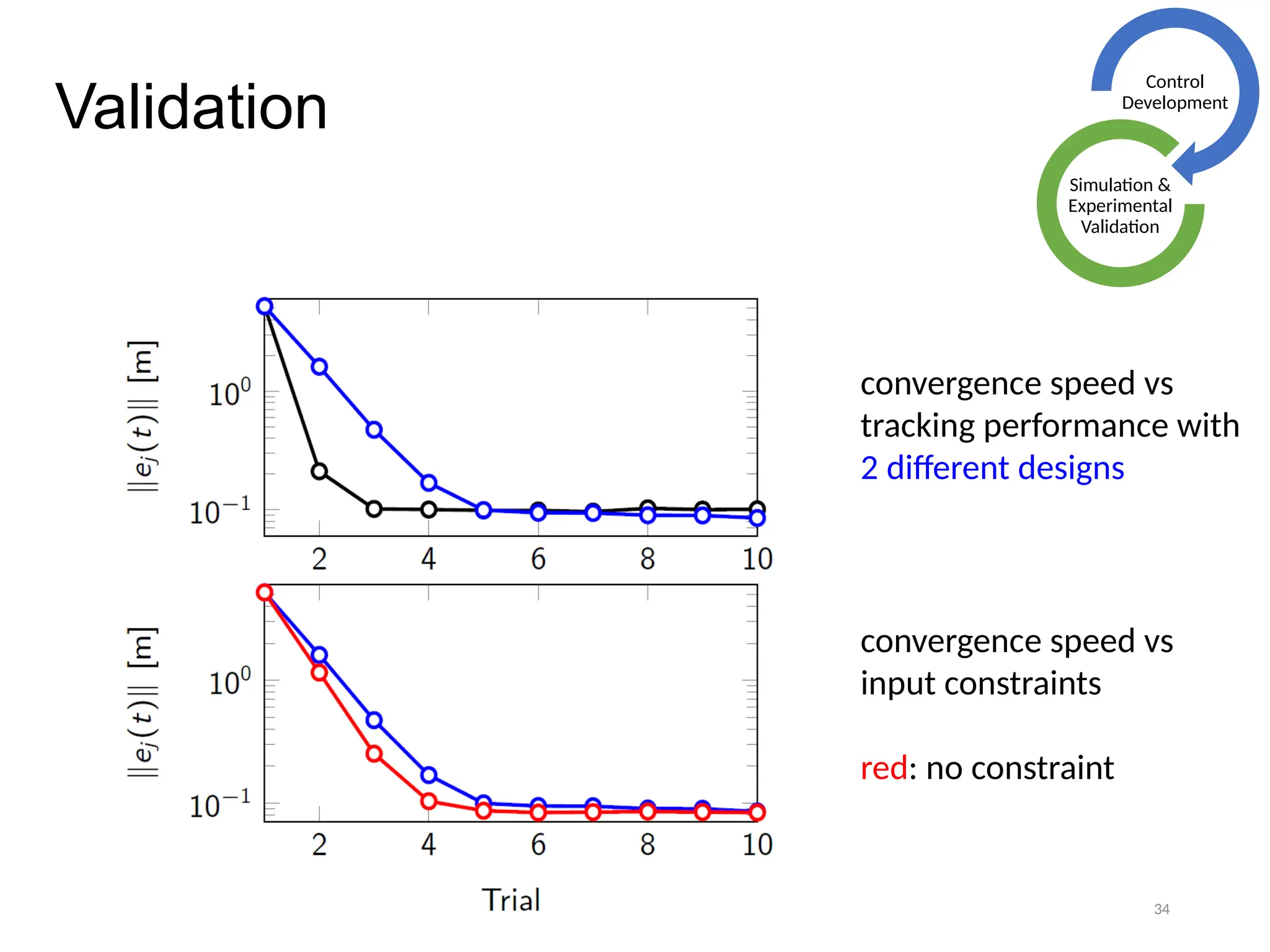
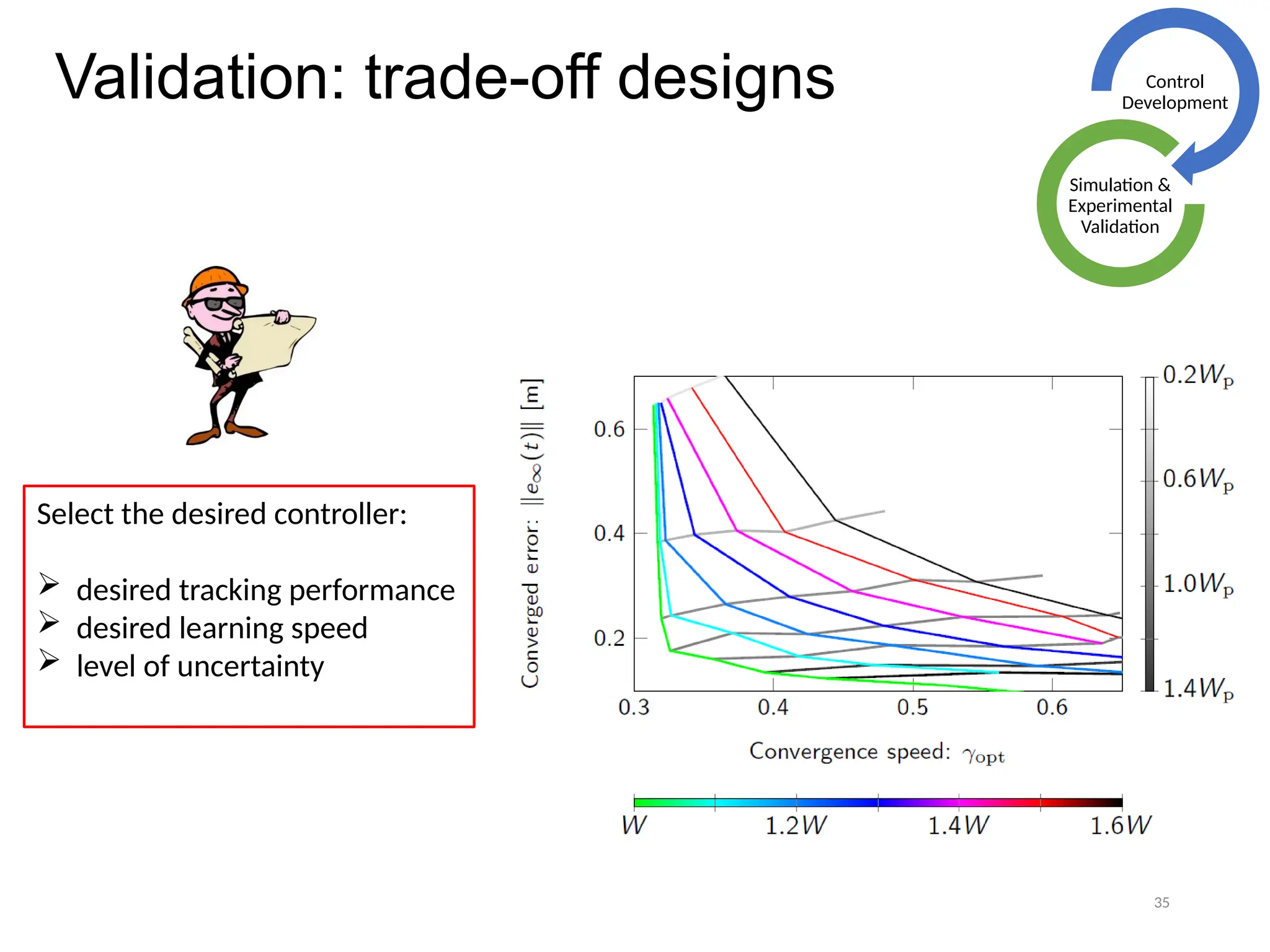
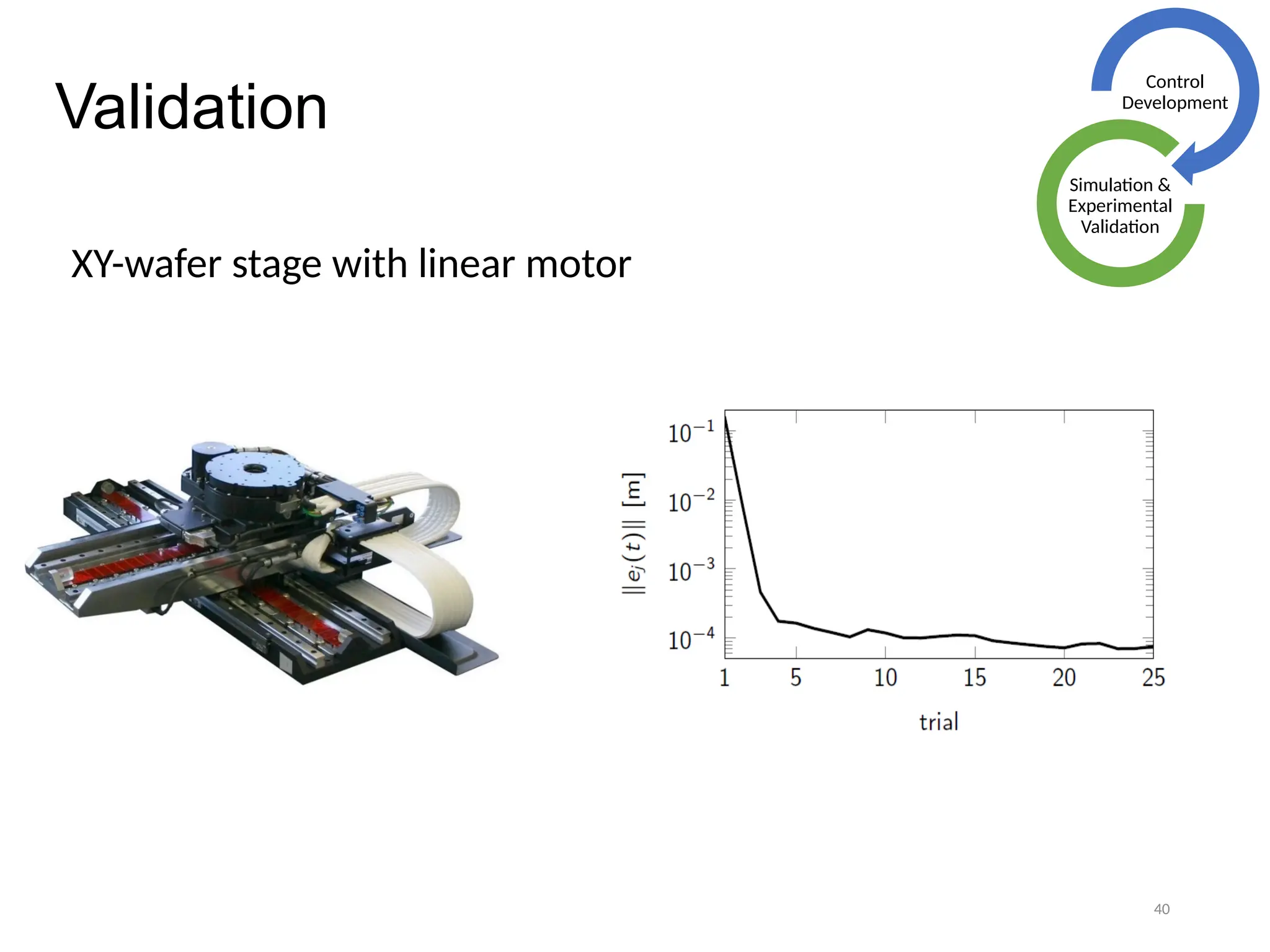
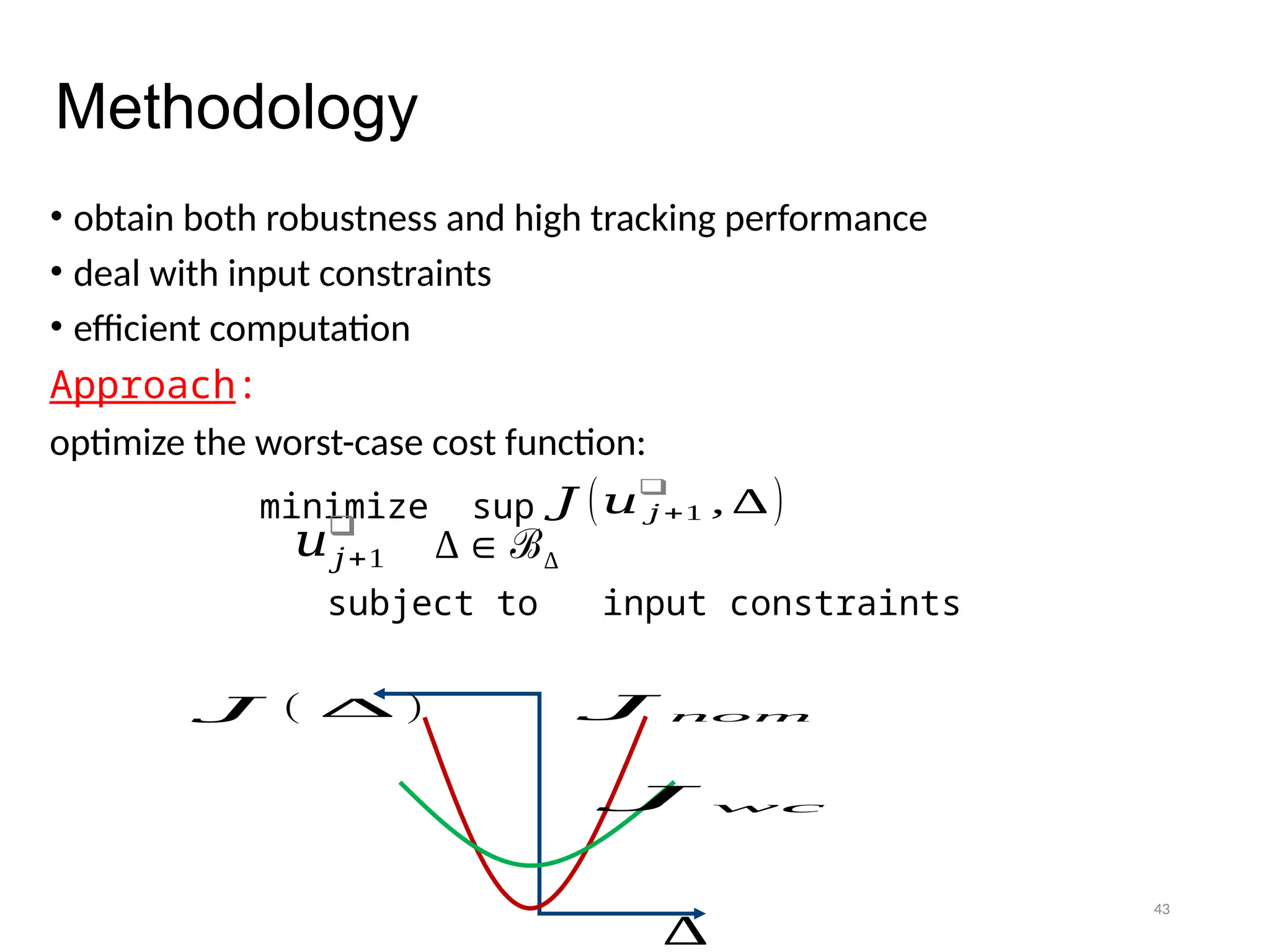
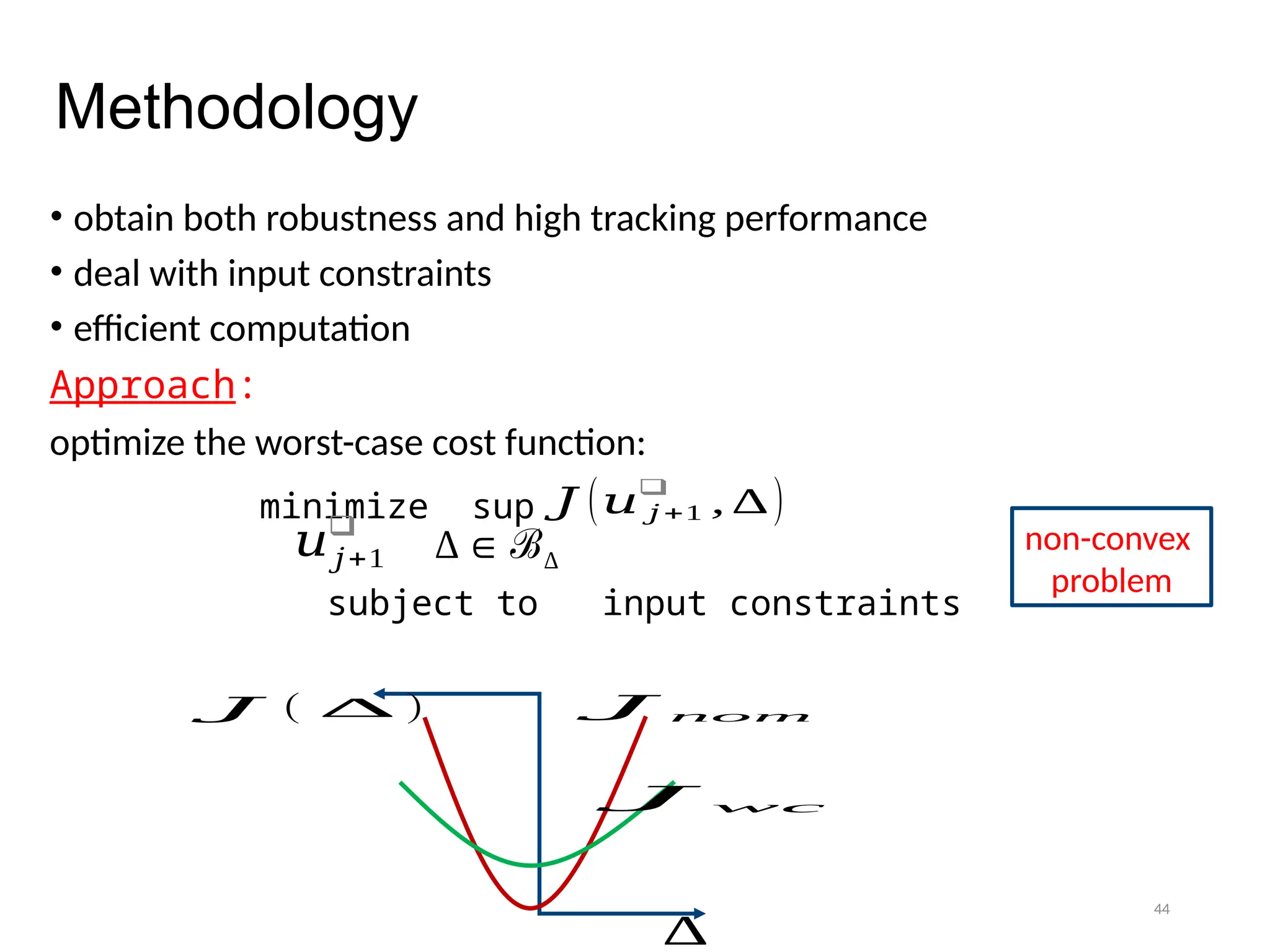
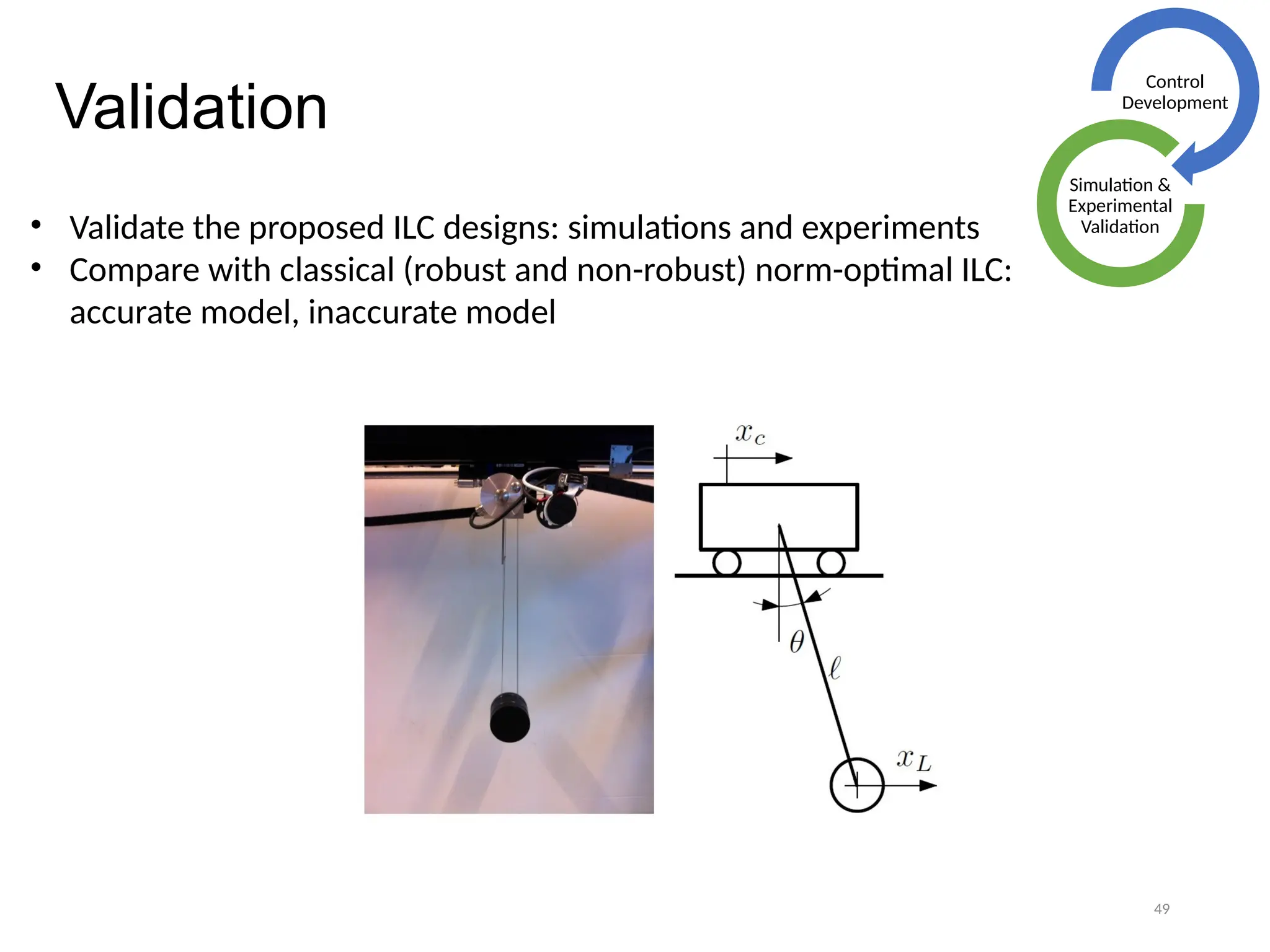
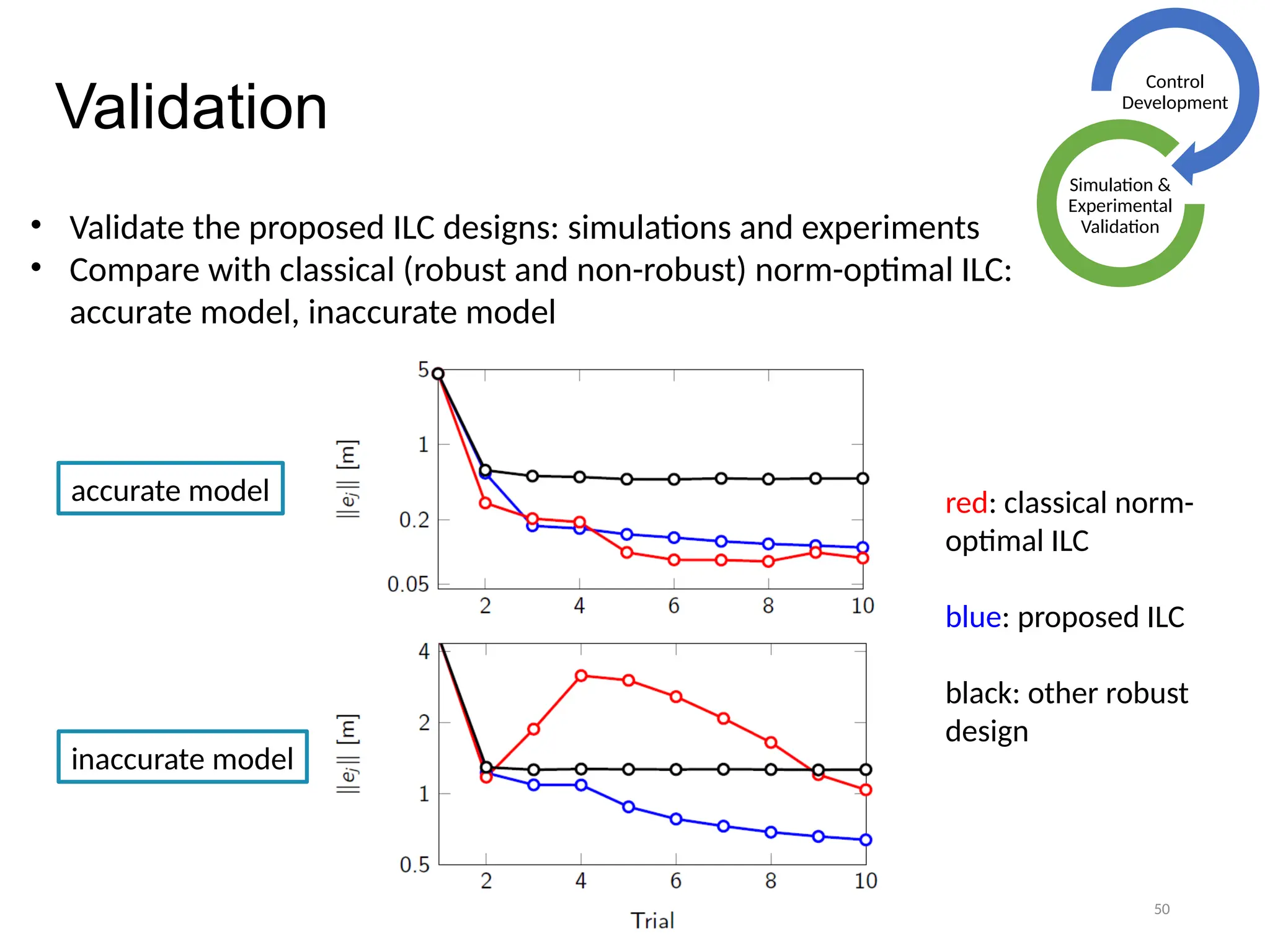
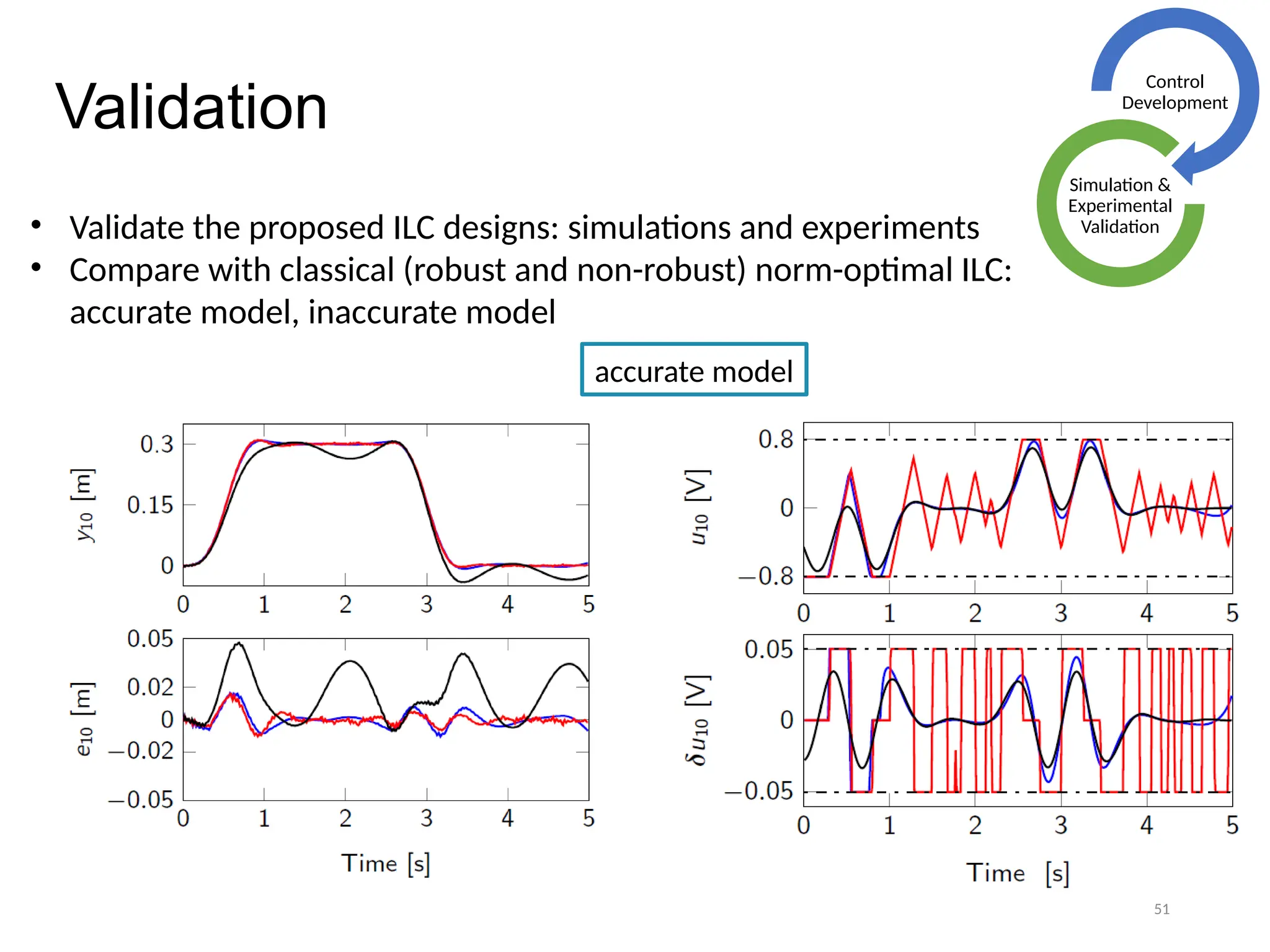
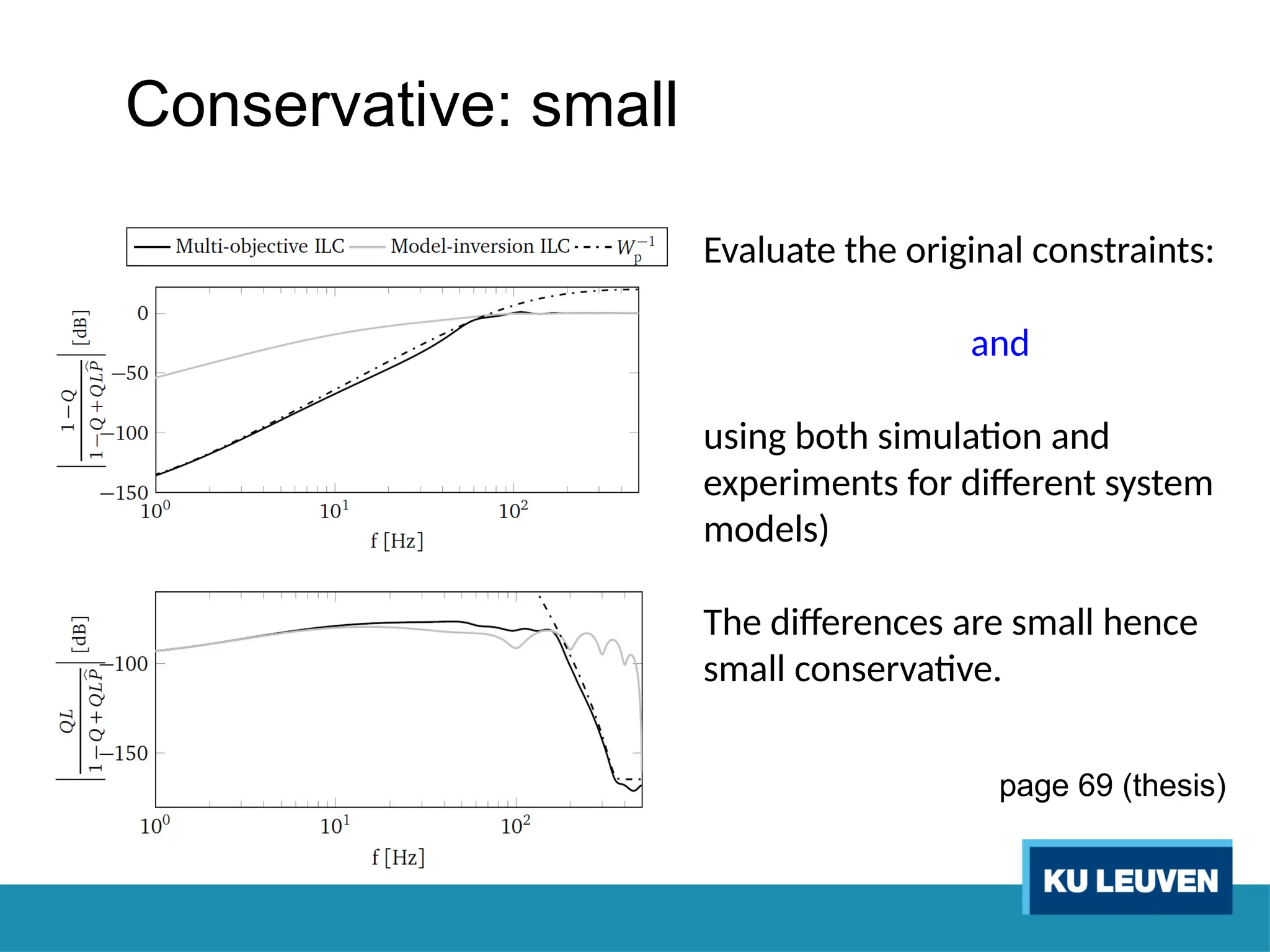
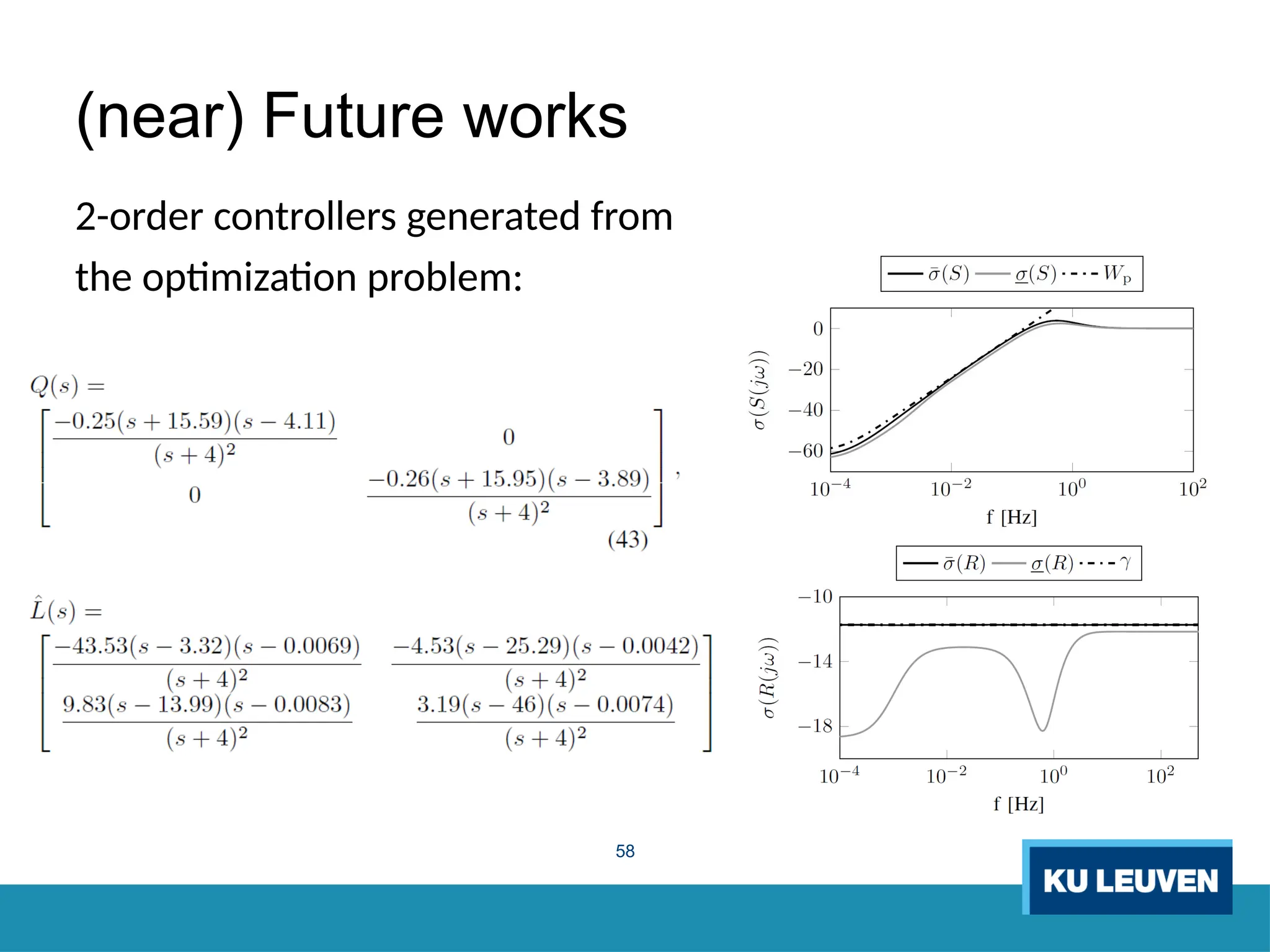
The thesis focuses on improving iterative learning control (ILC) systems through multi-objective optimization to enhance robustness, precision, and convergence while managing input constraints. It introduces novel methodologies for designing optimal ILC controllers that address challenges like model uncertainty and performance trade-offs. Extensive simulations and experiments validate the proposed designs and their advantages over traditional methods.