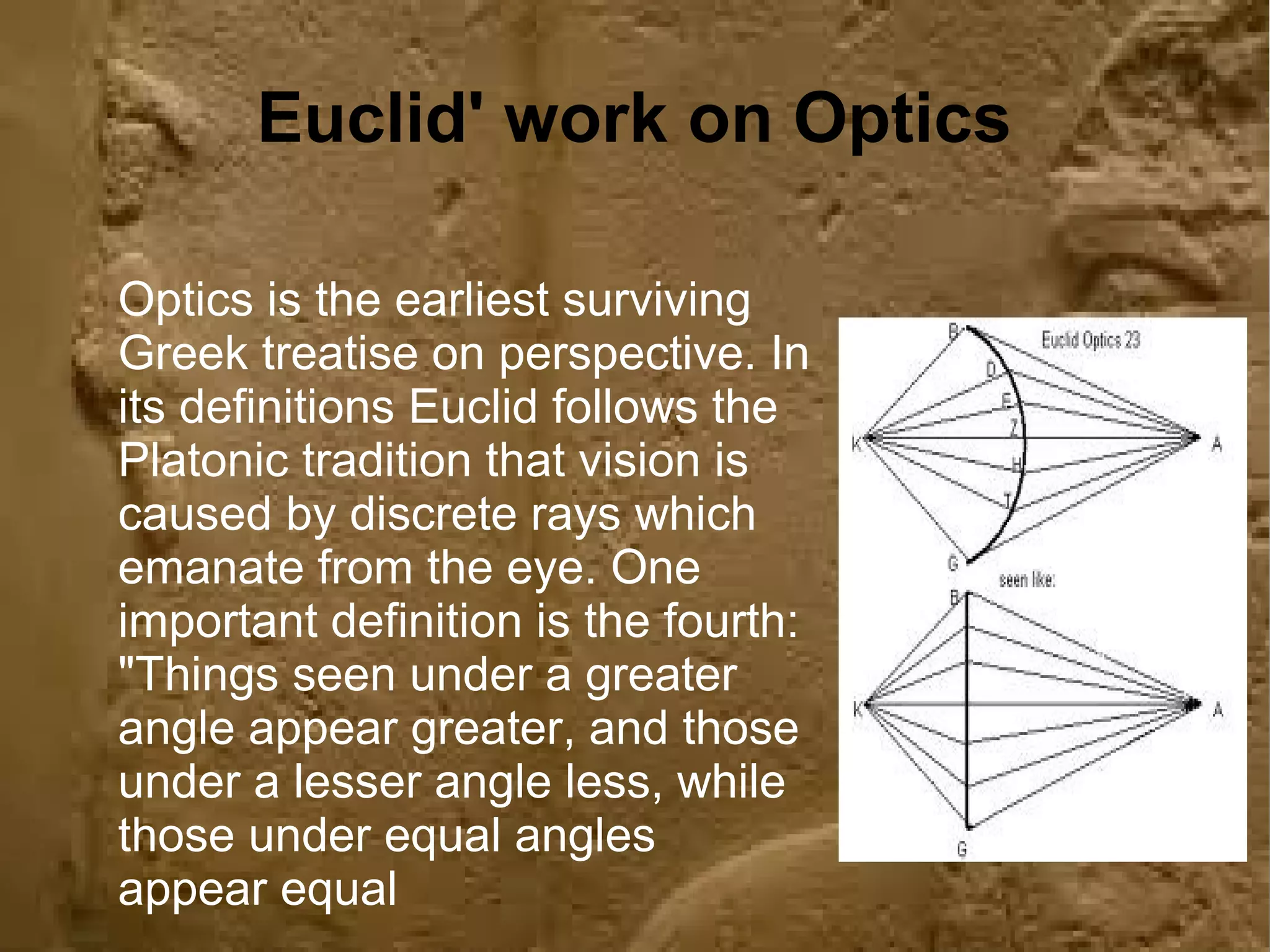
Euclid was a Greek mathematician from Alexandria known as the "Father of Geometry". His influential work Elements deduced the principles of Euclidean geometry from a small set of axioms. It served as the main textbook for teaching mathematics for over 2000 years. Euclid also wrote works on perspective, conic sections, spherical geometry, number theory, and rigor. He established an innovative deductive system in geometry based on definitions, axioms, and theorems and used it to prove various geometric results, such as how to construct a regular dodecahedron.