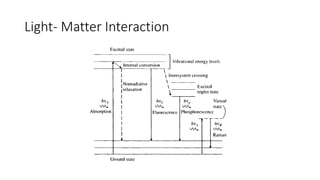
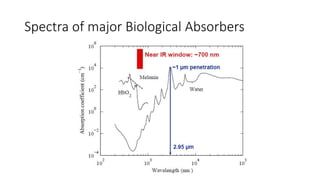
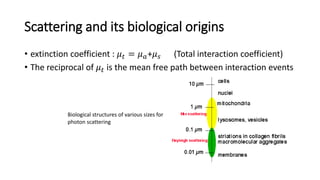
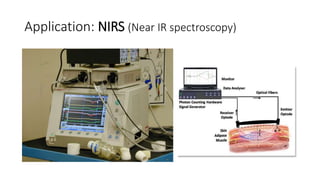
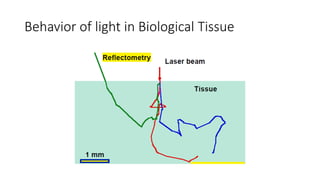
This document describes the syllabus for a biomedical optics course. It covers 13 topics including Monte Carlo modeling of photon transport, the radiative transfer equation, diffuse optical tomography, and ultrasound-modulated optical tomography. The first chapter introduces motivation for optical imaging in biology, general behavior of light in tissue, and basic light-matter interactions. It discusses optical properties of tissue, Beer's law, absorption and scattering origins and coefficients, and exercises calculating light transmission through absorbing and scattering media. Oxygen saturation and concentration are also introduced.

1. School of Engineering
Department of Biomedical Engineering
Fall 2014-2015
EENG624 – Biomedical Optics
Instructor: Jad AYOUB

2. Chapters
1. Introduction to biomedical optics
2. Single scattering: Rayleigh theory and Mie theory
3. Monte Carlo modeling of photon transport
4. Convolution for broad-beam responses
5. Radiative transfer equation and diffusion theory
6. Hybrid model of Monte Carlo method and diffusion theory
7. Sensing of optical properties and spectroscopy
8. Ballistic imaging and microscopy
9. Optical coherence tomography
10.Mueller optical coherence tomography
11.Diffuse optical tomography
12.Photoacoustic tomography
13.Ultrasound-modulated optical tomography

3. Chapter 1 - Introduction
• Motivation for Optical Imaging
• General Behavior of Light in Biological Tissue
• Basic Physics of Light-Matter Interaction

4. Motivation for Optical Imaging
1. Optical photons provide nonionizing and safe radiation for medical applications.
2. Optical spectra -based on absorption, fluorescence, or Raman scattering- provide biochemical
information because they are related to molecular conformation.
3. Optical absorption, in particular, reveals angiogenesis and hypermetabolism, both of which are
hallmarks of cancer; the former is related to the concentration of hemoglobin and the latter to the
oxygen saturation of hemoglobin. Therefore, optical absorption provides contrast for functional
imaging.
4. Optical scattering spectra provide information about the size distribution of optical scatterers,
such as cell nuclei.
5. Optical polarization provides information about structurally anisotropic tissue components,
such as collagen and muscle fiber.

5. Motivation for Optical Imaging (cont’d)
6. Optical frequency shifts due to the optical Doppler effect provide information about blood flow.
7. Optical properties of targeted contrast agents provide contrast for the molecular imaging of
biomarkers.
8. Optical properties or bioluminescence of products from gene expression provide contrast for
the molecular imaging of gene activities.
9. Optical spectroscopy permits simultaneous detection of multiple contrast agents.
10. Optical transparency in the eye provides a unique opportunity for high-resolution imaging of
the retina.

6. Behavior of light in Biological Tissue

7. Optical properties of biological tissue
Basic properties
• n [–]: index of refraction; e.g., 1.37
• μa [cm–1]: absorption coefficient; e.g., 0.1
• μs [cm–1]: scattering coefficient; e.g., 100
• g [–]: scattering anisotropy, <cosθ>; e.g., 0.9
Derived properties
• μt [cm–1]: total interaction (extinction) coefficient, μa + μs
• lt [cm]: mean free path, 1/ μt; e.g., 0.1 mm
• μs’ [cm–1]: reduced scattering coefficient, μs(1 – g)
• μt’ [cm–1]: transport interaction coefficient, μa + μs’
• lt’ [cm]: transport mean free path, 1/ μt’; e.g., 1 mm
• μeff [cm–1]: effective attenuation coefficient, (3μa μt’)1/2
• δ [cm]: penetration depth, 1/(3μa μt’)1/2; e.g., 5 mm

8. Light- Matter Interaction

9. Beer’s Law
• −
푑퐼/퐼
푑푥
= 휇푡
• 퐼 푥 = 퐼 0 푒−휇푡푥 = 퐼(0)푒−푥/푙푡
I : Ballistic intensity
x : Pathlength
휇푡: Total interaction (extinction) coefficient

10. Spectra of major Biological Absorbers

11. Absorption and its biological origins
• Absorption cross section: 휎푎
• Number of density: Na
• Absorption coefficient: total cross-sectional area for absorption per unit
volume:
휇푎 = 푁푎휎푎
• Light attenuates as it propagates in an absorbing medium:
푑퐼
퐼
= −휇푎푑푥
퐼 푥 = 퐼0푒−휇푎푥 : Beer’s law
• Transmittance: 푇 =
퐼(푥)
퐼0
: Probability of survival after propagation over 푥.

12. Absorption and its biological origins
• Origin of absorption:
oHemoglobin
(Oxygenated & de-Oxygenated)
oMelanin
oWater
Melanin absorbs (UV) light strongly
water can be highly absorbing in some spectral regions

13. Scattering and its biological origins
• Scattering cross section: 휎푠
• Number of density: Ns
• Scattering coefficient: total cross-sectional area for scattering per unit
volume:
휇푠 = 푁푠휎푠
• Light attenuates as it propagates in an Scattering medium:
푑퐼
퐼
= −휇푠푑푥
퐼 푥 = 퐼0푒−휇푠푥 : Beer’s law
• Transmittance: 푇 =
퐼(s)
퐼0
= 푒−휇푠푥 : Probability of survival after propagation
over 푥.

14. Scattering and its biological origins
• extinction coefficient : 휇푡 = 휇푎+휇푠 (Total interaction coefficient)
• The reciprocal of 휇푡 is the mean free path between interaction events
Biological structures of various sizes for
photon scattering

15. Exercise 1
• In a purely absorbing (non-scattering) medium with absorption
coefficient 휇푎, what percentage of light is left after a lightbeam
propagates a length of L?

16. Exercise 1
• In a purely absorbing (non-scattering) medium with absorption
coefficient 휇푎, what percentage of light is left after a lightbeam
propagates a length of L?

17. Exercise 2
• In a purely absorbing (non-scattering) medium with absorption
coefficient 휇푎, Derive the average length of survival of a photon?

18. Exercise 2
• In a purely absorbing (non-scattering) medium with absorption
coefficient 휇푎, Derive the average length of survival of a photon?

19. Exercise 3
• In a purely scattering (non-absorbing) medium with scattering
coefficient 휇푠, what percentage of light has not been scattered after
the original lightbeam propagates a length of L?

20. Exercise 3
• In a purely scattering (non-absorbing) medium with scattering
coefficient 휇푠, what percentage of light has not been scattered after
the original lightbeam propagates a length of L?

21. Exercise 4
• In a purely scattering (non-absorbing) medium with scattering
coefficient 휇푠, Derive the average length of survival of a photon.

22. Exercise 4
• In a purely scattering (non-absorbing) medium with scattering
coefficient 휇푠, Derive the average length of survival of a photon.

23. Exercise 5
• In a scattering medium with absorption coefficient 휇푎 and scattering
coefficient 휇푠 , what percentage of light has survived scattering and
absorption after the original lightbeam propagates a length of L? Of
the percentage that has been absorbed and scattered, what is the
percentage that has been absorbed?

24. Oxygen Saturation and Concentration
• Estimating concentration by absorption coefficients (@ 휆1 ≠ 휆2):
• 휆1 , 휆2 : the two wavelengths
• 휀표푥 , 휀푑푒: Molar extinction coefficients of oxy- and deoxyhemoglobin
• 퐶표푥 , 퐶푑푒: Molar concentrations of oxy- and deoxyhemoglobin.

25. Oxygen Saturation and Concentration
• Once 퐶표푥 and 퐶푑푒 are obtained, the oxygen saturation (푆푂2) and the
total concentration (퐶퐻퐵 ) of hemoglobin can be computed as follows:
• This principle provides the basis for pulse oximetry and functional
imaging. Angiogenesis can increase 퐶퐻퐵, whereas tumor
hypermetabolism can decrease 푆푂2.

26. Application: NIRS (Near IR spectroscopy)