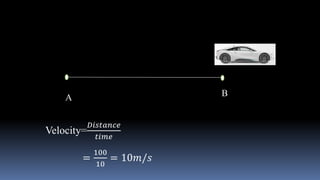
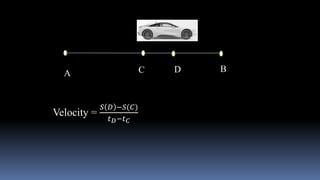
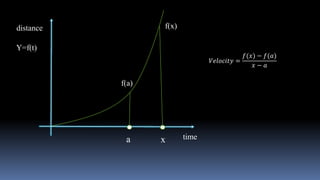
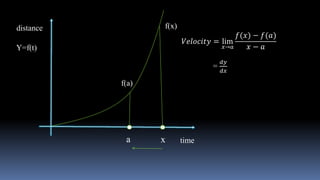
This document provides an introduction to differential equations. It defines key terms like differentiation, dependent and independent variables, ordinary and partial differential equations. Differentiation is defined as how a quantity changes with respect to changes in another quantity. A differential equation is an equation that contains differential coefficients. Ordinary differential equations contain a single independent variable, while partial differential equations contain at least two independent variables. Examples of both types of differential equations are provided. The document also discusses the concepts of dependent and independent variables. The dependent variables in an equation are the variables being solved for, while the independent variables are the variables with respect to which the dependent variables change.

1. V.V. VANNIAPERUMAL COLLEGE FOR WOMEN
Introduction of Differential Equation
Dr. T. Anitha
Assistant Professor
Department of Mathematics(SF)

2. A B
Distance traveled from A to B is S=100m
Time taken to travel t=10s

3. A B
Velocity=
𝐷𝑖𝑠𝑡𝑎𝑛𝑐𝑒
𝑡𝑖𝑚𝑒
=
100
10
= 10𝑚/𝑠

4. A B
Velocity =
𝑆 𝐷 −𝑆(𝐶)
𝑡𝐷−𝑡𝐶
C D

5. time
distance
a x
Y=f(t)
f(a)
f(x)
𝑉𝑒𝑙𝑜𝑐𝑖𝑡𝑦 =
𝑓(𝑥) − 𝑓(𝑎)
𝑥 − 𝑎

6. time
distance
a x
Y=f(t)
f(a)
f(x)
𝑉𝑒𝑙𝑜𝑐𝑖𝑡𝑦 = lim
𝑥→𝑎
𝑓(𝑥) − 𝑓(𝑎)
𝑥 − 𝑎
=
𝑑𝑦
𝑑𝑥

7. Differentiation
Differentiation is how rapidly that quantity changes with respect to change
in another quantity.
Differential Equation
Differential equation is an equation in which differential coefficient occur.

8. Examples:
Differential equations are of two types:
 Ordinary differential equation
Partial differential equation
1. y’ + 2𝑦 + 3𝑥 = 0
2.
𝑑2𝑦
𝑑𝑥2 + 𝑚2
𝑦 = 0

9. Dependent and independent variable
S
𝐴𝑟𝑒𝑎 = 𝑆2
S+d
𝐴𝑟𝑒𝑎 = 𝑆 + 𝑑 2
So Area is a function of side (s)
Therefore area 𝐴 = 𝑓(𝑆) = 𝑆2
The perimeter P=f(S)=4s
Hence in the variables A, P, S,
A and P are dependent variables and
S is the independent variable.

10. Dependent and independent variable
L
Area=BL
L+d
Area=(L+d)(B+r)
B
B+r
So Area of a rectangle
is a function of length (L) and breath (B)
Therefore area A=f(B,L)=BL
The perimeter P=f(B,L)=2(B+L)
Hence, in the variables A, P, B, L
A and P are dependent variables and
L, B are the independent variables.

11. Ordinary differentiation
 y=f(x)

𝑑𝑦
𝑑𝑥
(rate of change of y w.r.t x)
Partial differentiation
 y=f(x,z)

𝜕𝑦
𝜕𝑥
(rate of change of y w.r.t x)

𝜕𝑦
𝜕𝑧
(rate of change of y w.r.t z)

12. Ordinary differential equation
An ordinary differential equation is an equation in which a single independent
variable enters either explicitly or implicitly
Example
1.
𝑑𝑦
𝑑𝑥
= 2 𝑠𝑖𝑛𝑥 (Here x is independent variable and y is dependent variable)
2.
𝑑2𝑦
𝑑𝑡2 = 𝑚2𝑥 (Here t is independent variable and x, y are dependent variable)

13. Partial differential equation
A partial differential equation is an equation in which at least two or more independent
variables enter and partial coefficient occurring in them.
Example
x
𝜕𝑧
𝜕𝑥
+ 𝑦
𝜕𝑧
𝜕𝑦
= 𝑧 (Here x,y are independent variable and z is dependent variable)

14. Thank you