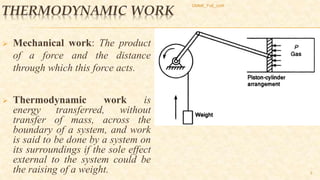
This document discusses thermodynamic concepts including internal energy, enthalpy, and thermodynamic work. It provides definitions and equations for calculating the internal energy and enthalpy of ideal gases, liquids, and solids. For ideal gases, the internal energy and enthalpy depend only on temperature. For incompressible liquids and solids, the specific heat is constant and the change in internal energy can be calculated using the average temperature. The document includes two example problems applying these concepts to calculate temperature changes in systems.

1. Dr.(Mrs.) K.T.K.M. De Silva
Department of Mechanical and Manufacturing Engineering
ME2201 – FUNDAMENTALS
OF ENGINEERING
THERMODYNAMICS

2. INTERNAL ENERGY AND
ENTHALPY

3. THERMODYNAMIC WORK
 Thermodynamic work is
energy transferred, without
transfer of mass, across the
boundary of a system, and work
is said to be done by a system on
its surroundings if the sole effect
external to the system could be
the raising of a weight.
DMME_FoE_UoR
3
 Mechanical work: The product
of a force and the distance
through which this force acts.

4. INTERNAL ENERGY OF IDEAL GASES
DMME_FoE_UoR
4
𝐼𝑑𝑒𝑎𝑙 𝑔𝑎𝑠 𝑠𝑡𝑎𝑡𝑒 𝑒𝑞𝑢𝑎𝑡𝑖𝑜𝑛: 𝑃𝑣 = 𝑅𝑇
𝐼𝑛𝑡𝑒𝑟𝑛𝑎𝑙 𝑒𝑛𝑒𝑟𝑔𝑦 𝑜𝑓 𝑎𝑛 𝑖𝑑𝑒𝑎𝑙 𝑔𝑎𝑠: 𝑢 = 𝑢(𝑇)
𝐸𝑛𝑡ℎ𝑎𝑙𝑝𝑦 𝑜𝑓 𝑎𝑛 𝑖𝑑𝑒𝑎𝑙 𝑔𝑎𝑠: ℎ = 𝑢 + 𝑃𝑣
ℎ = 𝑢 + 𝑅𝑇
ℎ = ℎ(𝑇)
𝐴𝑡 𝑎 𝑔𝑖𝑣𝑒𝑛 𝑡𝑒𝑚𝑝𝑒𝑟𝑎𝑡𝑢𝑟𝑒, 𝑢, ℎ, 𝐶𝑣, 𝐶𝑝 𝑜𝑓 𝑎𝑛 𝑖𝑑𝑒𝑎𝑙 𝑔𝑎𝑠 ℎ𝑎𝑣𝑒 𝑓𝑖𝑥𝑒𝑑
𝑣𝑎𝑙𝑢𝑒𝑠

5. INTERNAL ENERGY OF IDEAL GASES…
DMME_FoE_UoR
5
𝑑𝑢 = 𝐶𝑣 𝑇 𝑑𝑇 𝑑ℎ = 𝐶𝑝 𝑇 𝑑𝑇
∆𝑢 = 𝑢2 − 𝑢1 = 1
2
𝐶𝑣 𝑇 𝑑𝑇 ∆ℎ = ℎ2 − ℎ1 = 1
2
𝐶𝑝 𝑇 𝑑𝑇
Differential changes in the internal energy and enthalpy of an ideal gas:
The change in u and h for an ideal gas during a process from state 1 to state 2 is
determined by integrating:
Specific heat ratio:
𝛾 =
𝐶𝑝
𝐶𝑣

6. INTERNAL ENERGY OF LIQUID AND SOLID
DMME_FoE_UoR
6
Incompressible substances: the specific volume essentially remains constant during a
process. The energy associated with the volume change, such as the boundary work, is
negligible compared to other forms of energy.
𝐶𝑝 = 𝐶𝑣 = 𝐶
The specific heats for solids and liquids depend on temperature only.
𝑑𝑢 = 𝐶𝑣 𝑇 𝑑𝑇 = 𝐶 𝑇 𝑑𝑇
The change in internal energy during a process from state 1 to state 2 is,
∆𝑢 = 𝑢2 − 𝑢1 = 1
2
𝐶 𝑇 𝑑𝑇 ∆𝑢 ≈ 𝐶𝑎𝑣(𝑇2 − 𝑇1)

7. INTERNAL ENERGY OF LIQUID AND SOLID…
DMME_FoE_UoR
7
The change in enthalpy during a process from state 1 to state 2 can be determined
from the definition of enthalpy.
ℎ2 − ℎ1 = 𝑢2 − 𝑢1 + 𝑣(𝑃2 − 𝑃1)
Since 𝑣1 = 𝑣2 = 𝑣 for incompressible substances.
∆ℎ = ∆𝑢 + 𝑣∆𝑃

8. EXAMPLE 01
DMME_FoE_UoR
8
A 0.6 kg copper piece at 100 °C is dropped in an insulated rigid tank which
contains 0.75 kg of liquid water at 25°C. Determine the temperature of the
system when thermal equilibrium is established. Take specific heats of
copper and water to be 0.393 kJ/(kg K) and 4.184 kJ/(kg K), respectively.

9. EXAMPLE 02
In a piston-cylinder device, 300 g of saturated water vapour, maintained at
200 kPa, is heated by a resistance heater installed within the cylinder for
10 min by passing a current of 0.35 ampere from a 220 V source. The heat
loss from the system during the heating process is 2.2 kJ. Calculate the
work done and the final temperature of the steam.
DMME_FoE_UoR
9