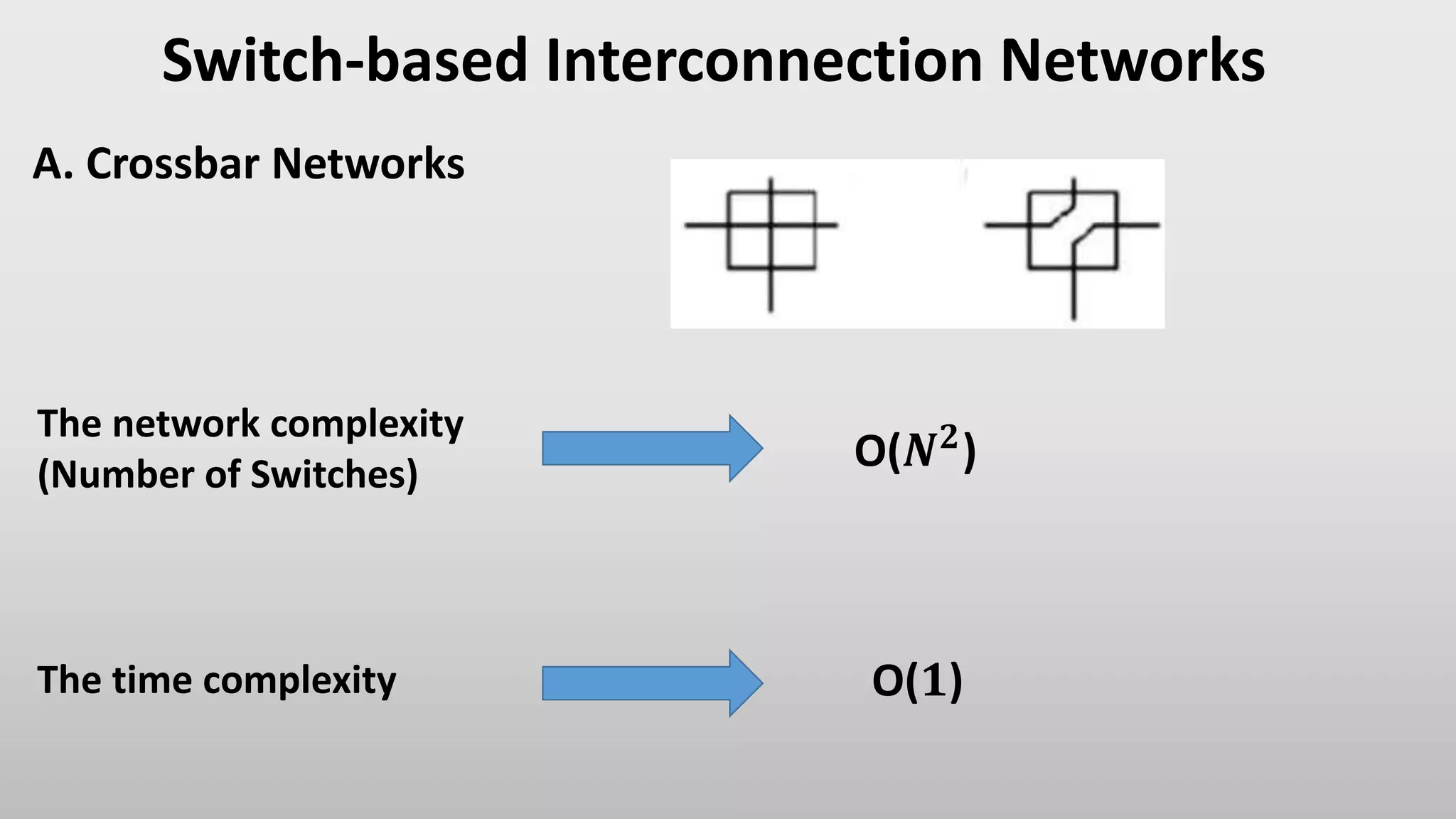
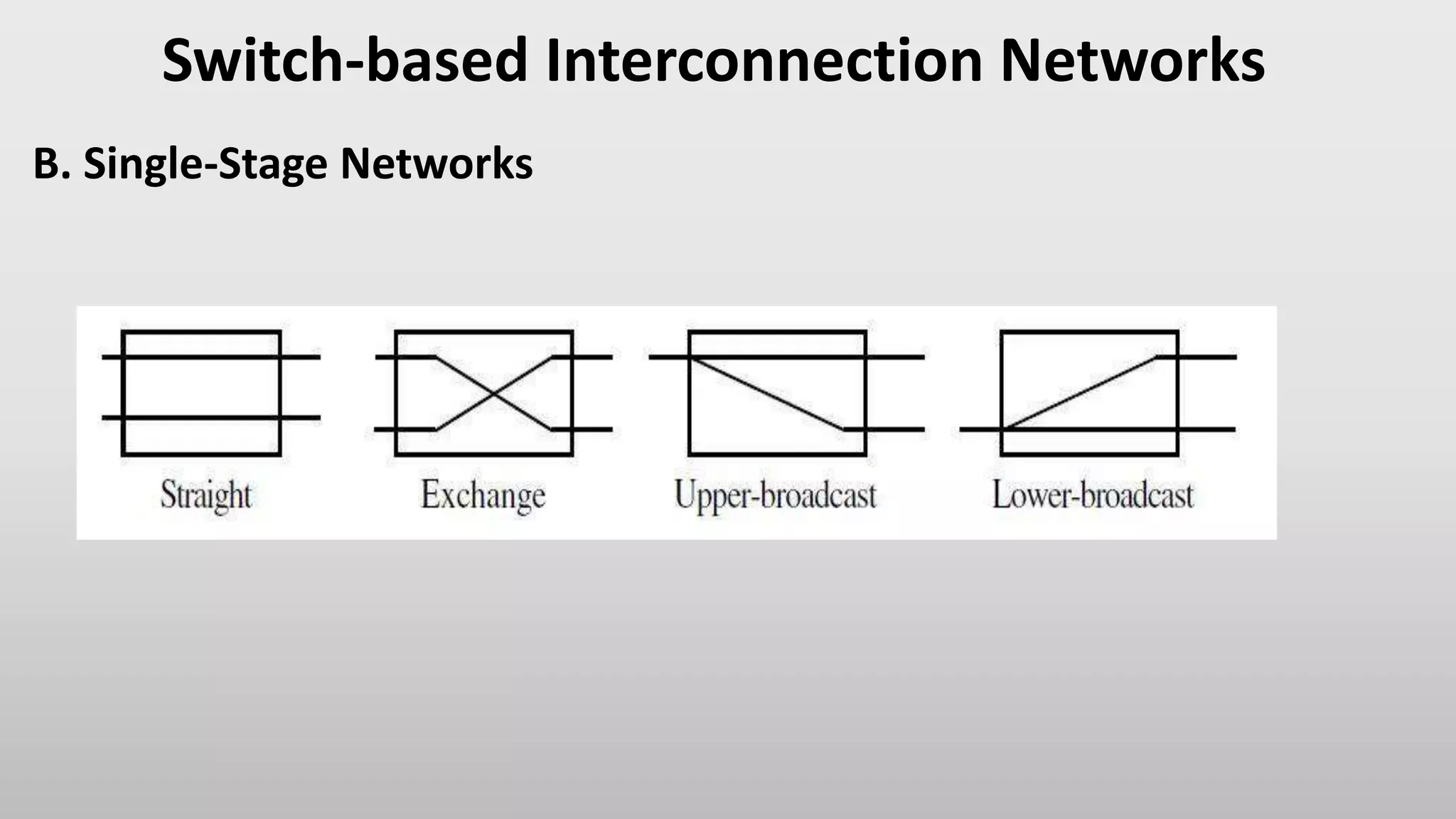
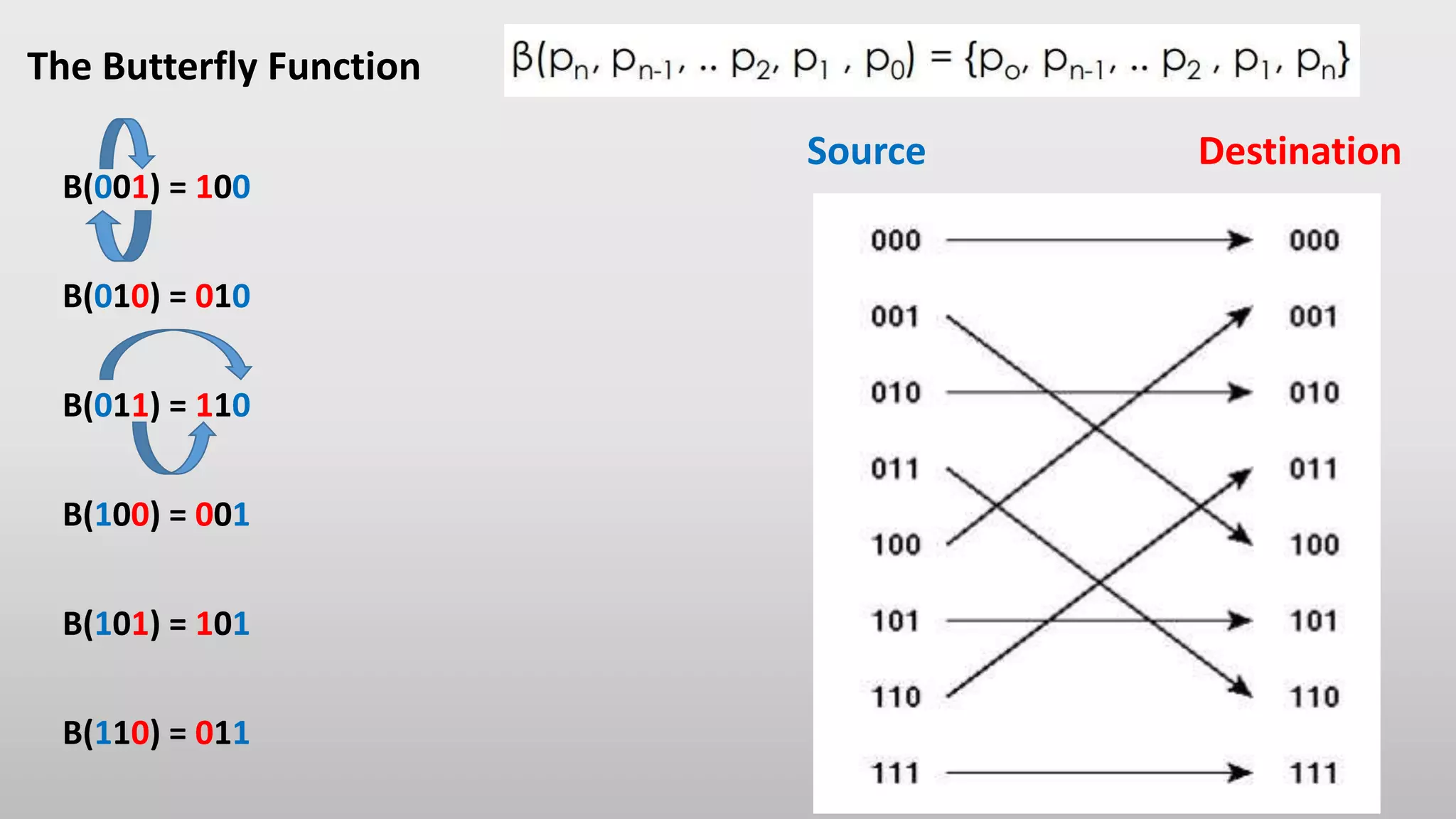
The document discusses and provides examples of different types of single-stage interconnection networks, including shuffle-exchange networks, cube networks, plus-minus networks, and butterfly networks. Specifically, it shows how sources and destinations are mapped in each type of network by applying routing functions like shuffling bits, adding/subtracting modulo the number of nodes, and bit-reversal. These single-stage networks provide constant-time routing but require more switches than crossbar networks.

1. Interconnection Networks

2. Switch-based Interconnection Networks
A. Crossbar Networks
The network complexity
(Number of Switches)
O(𝑵𝟐
)
The time complexity O(𝟏)

3. Switch-based Interconnection Networks
B. Single-Stage Networks

4. B. Single-Stage Networks
Shuffle – Exchange
000 001 010 011 110
Source 0( 000)
Destination 6(110)
Source
Destination
E S E S
0 1 2 3 6
First bit ‫تبديل‬
‫اليسار‬ ‫الى‬ ‫تحريك‬

5. Shuffle – Exchange ( ‫تنافسي‬
2018 )
Source 4 (100)
Destination 7 (111)
Source
Destination
S(100)  1(001)  E(001)  0(000)  S(000)  0(000)  E(000)  1(001) 
S(001)  2(010)  E(010)  3(011)  S(011)  6(110)  E (110)  7(111)
First bit ‫تبديل‬
‫اليسار‬ ‫الى‬ ‫تحريك‬

6. The Cube Network
Source Destination
𝑪𝟎(0) = 1
0 1
i 2 1 0
0 0 0 0
i 2 1 0
1 0 0 1
𝑪𝟎

7. The Cube Network
Source Destination
𝑪𝟎(4) = 5
4 5
i 2 1 0
4 1 0 0
i 2 1 0
5 1 0 1
𝑪𝟎

8. The Cube Network
Source Destination
𝑪𝟏(7) = 5
7 5
i 2 1 0
7 1 1 1
i 2 1 0
5 1 0 1
𝑪𝟏

9. The Cube Network
Source Destination
𝑪𝟐(6) = 2
6 2
i 2 1 0
6 1 1 0
i 2 1 0
2 0 1 0
𝑪𝟐

10. Source Destination
4 5
For example, consider the case N = 8, i = 0
𝑷𝑴𝟐+𝟎
(4) = 4 + 𝟐𝟎 mod 8 = 5
The Plus–Minus

11. Source Destination
4 6
For example, consider the case N = 8, i = 1
𝑷𝑴𝟐+𝟏
(4) = 4 + 𝟐𝟏 mod 8 = 6
The Plus–Minus

12. The Plus–Minus
Source Destination
7 3
For example, consider the case N = 8, i = 2
𝑷𝑴𝟐+𝟐
(7) = 7 + 𝟐𝟐 mod 8 = 3

13. The Butterfly Function
Source Destination
B(001) = 100
B(010) = 010
B(011) = 110
B(100) = 001
B(101) = 101
B(110) = 011