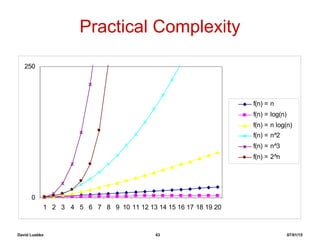
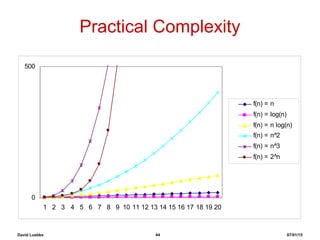
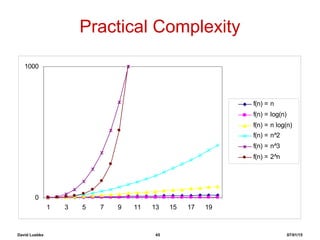
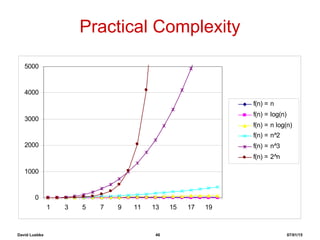
The document step-by-step demonstrates the insertion sort algorithm by running it on the sample array [30, 10, 40, 20]. It shows the state of the array and relevant variables after each iteration of the outer for loop. Each step switches the value of one element in the array to correctly sort it in ascending order. After running through all elements, the array is fully sorted as [10, 20, 30, 40].

1. David Luebke 1 07/01/15
Insertion Sort

2. David Luebke 2 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}

3. David Luebke 3 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
30 10 40 20
1 2 3 4
i = ∅ j = ∅ key = ∅
A[j] = ∅ A[j+1] = ∅

4. David Luebke 4 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
30 10 40 20
1 2 3 4
i = 2 j = 1 key = 10
A[j] = 30 A[j+1] = 10

5. David Luebke 5 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
30 30 40 20
1 2 3 4
i = 2 j = 1 key = 10
A[j] = 30 A[j+1] = 30

6. David Luebke 6 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
30 30 40 20
1 2 3 4
i = 2 j = 1 key = 10
A[j] = 30 A[j+1] = 30

7. David Luebke 7 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
30 30 40 20
1 2 3 4
i = 2 j = 0 key = 10
A[j] = ∅ A[j+1] = 30

8. David Luebke 8 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
30 30 40 20
1 2 3 4
i = 2 j = 0 key = 10
A[j] = ∅ A[j+1] = 30

9. David Luebke 9 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 2 j = 0 key = 10
A[j] = ∅ A[j+1] = 10

10. David Luebke 10 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 3 j = 0 key = 10
A[j] = ∅ A[j+1] = 10

11. David Luebke 11 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 3 j = 0 key = 40
A[j] = ∅ A[j+1] = 10

12. David Luebke 12 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 3 j = 0 key = 40
A[j] = ∅ A[j+1] = 10

13. David Luebke 13 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 3 j = 2 key = 40
A[j] = 30 A[j+1] = 40

14. David Luebke 14 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 3 j = 2 key = 40
A[j] = 30 A[j+1] = 40

15. David Luebke 15 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 3 j = 2 key = 40
A[j] = 30 A[j+1] = 40

16. David Luebke 16 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 4 j = 2 key = 40
A[j] = 30 A[j+1] = 40

17. David Luebke 17 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 4 j = 2 key = 20
A[j] = 30 A[j+1] = 40

18. David Luebke 18 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 4 j = 2 key = 20
A[j] = 30 A[j+1] = 40

19. David Luebke 19 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 4 j = 3 key = 20
A[j] = 40 A[j+1] = 20

20. David Luebke 20 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 20
1 2 3 4
i = 4 j = 3 key = 20
A[j] = 40 A[j+1] = 20

21. David Luebke 21 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 40
1 2 3 4
i = 4 j = 3 key = 20
A[j] = 40 A[j+1] = 40

22. David Luebke 22 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 40
1 2 3 4
i = 4 j = 3 key = 20
A[j] = 40 A[j+1] = 40

23. David Luebke 23 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 40
1 2 3 4
i = 4 j = 3 key = 20
A[j] = 40 A[j+1] = 40

24. David Luebke 24 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 40
1 2 3 4
i = 4 j = 2 key = 20
A[j] = 30 A[j+1] = 40

25. David Luebke 25 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 40 40
1 2 3 4
i = 4 j = 2 key = 20
A[j] = 30 A[j+1] = 40

26. David Luebke 26 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 30 40
1 2 3 4
i = 4 j = 2 key = 20
A[j] = 30 A[j+1] = 30

27. David Luebke 27 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 30 40
1 2 3 4
i = 4 j = 2 key = 20
A[j] = 30 A[j+1] = 30

28. David Luebke 28 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 30 40
1 2 3 4
i = 4 j = 1 key = 20
A[j] = 10 A[j+1] = 30

29. David Luebke 29 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 30 30 40
1 2 3 4
i = 4 j = 1 key = 20
A[j] = 10 A[j+1] = 30

30. David Luebke 30 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 20 30 40
1 2 3 4
i = 4 j = 1 key = 20
A[j] = 10 A[j+1] = 20

31. David Luebke 31 07/01/15
An Example: Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
10 20 30 40
1 2 3 4
i = 4 j = 1 key = 20
A[j] = 10 A[j+1] = 20
Done!

32. David Luebke 32 07/01/15
Animating Insertion Sort
• Check out the Animator, a java applet at:
http://www.cs.hope.edu/~alganim/animator/Animator.html
• Try it out with random, ascending, and
descending inputs

33. David Luebke 33 07/01/15
Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
What is the precondition
for this loop?

34. David Luebke 34 07/01/15
Insertion Sort
InsertionSort(A, n) {
for i = 2 to n {
key = A[i]
j = i - 1;
while (j > 0) and (A[j] > key) {
A[j+1] = A[j]
j = j - 1
}
A[j+1] = key
}
}
How many times will
this loop execute?

35. David Luebke 35 07/01/15
Insertion Sort
Statement Effort
InsertionSort(A, n) {
for i = 2 to n { c1n
key = A[i] c2(n-1)
j = i - 1; c3(n-1)
while (j > 0) and (A[j] > key) { c4T
A[j+1] = A[j] c5(T-(n-1))
j = j - 1 c6(T-(n-1))
} 0
A[j+1] = key c7(n-1)
} 0
}
T = t2 + t3 + … + tn where ti is number of while expression evaluations for the ith
for

36. David Luebke 36 07/01/15
Analyzing Insertion Sort
• T(n) = c1n + c2(n-1) + c3(n-1) + c4T + c5(T - (n-1)) + c6(T - (n-1)) + c7(n-1)
= c8T + c9n + c10
• What can T be?
 Best case -- inner loop body never executed
o ti = 1  T(n) is a linear function
 Worst case -- inner loop body executed for all
previous elements
o ti = i  T(n) is a quadratic function
 Average case
o ???

37. David Luebke 37 07/01/15
Analysis
• Simplifications
 Ignore actual and abstract statement costs
 Order of growth is the interesting measure:
o Highest-order term is what counts
Remember, we are doing asymptotic analysis
As the input size grows larger it is the high order term that
dominates

38. David Luebke 38 07/01/15
Upper Bound Notation
• We say InsertionSort’s run time is O(n2
)
 Properly we should say run time is in O(n2
)
 Read O as “Big-O” (you’ll also hear it as “order”)
• In general a function
 f(n) is O(g(n)) if there exist positive constants c
and n0 such that f(n) ≤ c ⋅ g(n) for all n ≥ n0
• Formally
 O(g(n)) = { f(n): ∃ positive constants c and n0 such
that f(n) ≤ c ⋅ g(n) ∀ n ≥ n0

39. David Luebke 39 07/01/15
Insertion Sort Is O(n2
)
• Proof
 Suppose runtime is an2
+ bn + c
o If any of a, b, and c are less than 0 replace the constant
with its absolute value
 an2
+ bn + c ≤ (a + b + c)n2
+ (a + b + c)n + (a + b + c)
 ≤ 3(a + b + c)n2
for n ≥ 1
 Let c’ = 3(a + b + c) and let n0 = 1
• Question
 Is InsertionSort O(n3
)?
 Is InsertionSort O(n)?

40. David Luebke 40 07/01/15
Big O Fact
• A polynomial of degree k is O(nk
)
• Proof:
 Suppose f(n) = bknk
+ bk-1nk-1
+ … + b1n + b0
o Let ai = | bi|
 f(n) ≤ aknk
+ ak-1nk-1
+ … + a1n + a0
k
i
k
k
i
i
k
cnan
n
n
an ≤≤≤ ∑∑

41. David Luebke 41 07/01/15
Lower Bound Notation
• We say InsertionSort’s run time is Ω(n)
• In general a function
 f(n) is Ω(g(n)) if ∃ positive constants c and n0 such
that 0 ≤ c⋅g(n) ≤ f(n) ∀ n ≥ n0
• Proof:
 Suppose run time is an + b
o Assume a and b are positive (what if b is negative?)
 an ≤ an + b

42. David Luebke 42 07/01/15
Asymptotic Tight Bound
• A function f(n) is Θ(g(n)) if ∃ positive
constants c1, c2, and n0 such that
c1 g(n) ≤ f(n) ≤ c2 g(n) ∀ n ≥ n0
• Theorem
 f(n) is Θ(g(n)) iff f(n) is both O(g(n)) and Ω(g(n))
 Proof: someday

43. David Luebke 43 07/01/15
Practical Complexity
0
250
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
f(n) = n
f(n) = log(n)
f(n) = n log(n)
f(n) = n^2
f(n) = n^3
f(n) = 2^n

44. David Luebke 44 07/01/15
Practical Complexity
0
500
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
f(n) = n
f(n) = log(n)
f(n) = n log(n)
f(n) = n^2
f(n) = n^3
f(n) = 2^n

45. David Luebke 45 07/01/15
Practical Complexity
0
1000
1 3 5 7 9 11 13 15 17 19
f(n) = n
f(n) = log(n)
f(n) = n log(n)
f(n) = n^2
f(n) = n^3
f(n) = 2^n

46. David Luebke 46 07/01/15
Practical Complexity
0
1000
2000
3000
4000
5000
1 3 5 7 9 11 13 15 17 19
f(n) = n
f(n) = log(n)
f(n) = n log(n)
f(n) = n^2
f(n) = n^3
f(n) = 2^n

47. David Luebke 47 07/01/15
Practical Complexity
1
10
100
1000
10000
100000
1000000
10000000
1 4 16 64 256 1024 4096 16384 65536

48. David Luebke 48 07/01/15
Other Asymptotic Notations
• A function f(n) is o(g(n)) if ∃ positive
constants c and n0 such that
f(n) < c g(n) ∀ n ≥ n0
• A function f(n) is ω(g(n)) if ∃ positive
constants c and n0 such that
c g(n) < f(n) ∀ n ≥ n0
• Intuitively,
 o() is like <
 O() is like ≤
 ω() is like >
 Ω() is like ≥
 Θ() is like =

49. David Luebke 49 07/01/15
Up Next
• Solving recurrences
 Substitution method
 Master theorem