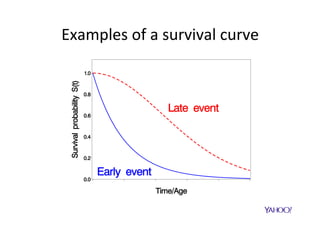
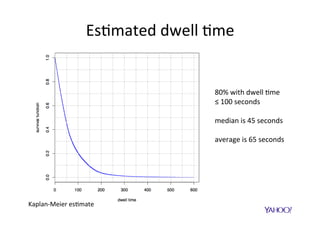
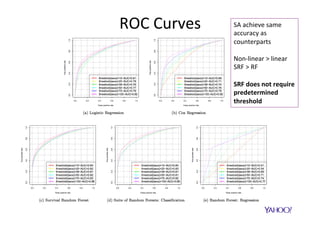
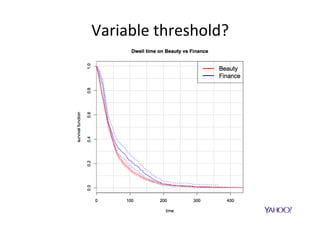
The document discusses improving user engagement on mobile native ads by using survival analysis to estimate post-click engagement metrics such as dwell time. It describes how to select ads based on predicted performance and introduces a survival random forest model, which assesses user retention and engagement. The results demonstrate improved user experience metrics, such as increased click-through rates and reduced bounce rates, highlighting potential for personalized advertising strategies in the future.

1. Improving Post-Click User
Engagement on Native Ads via
Survival Analysis
Nicola Barbieri, Fabrizio Silvestri and Mounia Lalmas

2. Na$ve ads and user engagement
• Es$mate post-click engagement on
mobile na$ve ads
• Integrate predic$on into ranking func$on
to promote the most engaging ads

3. • We measure
engagement by analyzing
what happens a0er the
user click:
– How much $me the user
spends on the landing
page?
• Two possibili$es:
– the user immediately
comes back (bounces)
– the user stays longer and
“hopefully” convert (high
dwell $me)
looser winner
Dwell $me based user engagement

4. How are na$ve ads selected?
?
?
?
?

5. ?
?
?
• It depends on
poten$al revenue:
eCPM = P(click) * bid
– P(click) is the
probability of user
clicking on an ad.
– Bid is the amount of
money the adver$ser
is willing to pay for
ad being shown.
How are na$ve ads selected?

6. eCPM = 0.1
eCPM = 0.08
eCPM = 0.05
How are na$ve ads selected?

7. Now consider dwell $me
• Suppose we can es$mate
pt = P(dwell_5me > t):
– Probability that a user will
stay for more than t seconds
on the ad landing page.
• We modify eCPM by
mul$plying it by pt
– In prac$ce we are compu$ng
probability of clicking AND
staying for more than t
seconds.

8. How to es$mate pt?
• If t is fixed a-priori it is, basically, a classifica$on
problem:
– Logis$c Regression
– Random Forest
– …
• What if we want to use different thresholds
depending on factors such as, users, ad category,
etc.?
– Different ad-hoc models
– Survival Analysis!

9. Survival Analysis
• Stems from the necessity of making a prognosis
for specific pa$ents, i.e., to es$mate the
probability of surviving a specific amount of $me.
• In other contexts, the response is not ‘survival’,
but a 8me to event:
– How long will a bulb ‘survive’
– Time un$l first tooth is affected with caries
– Time un$l a hard drive will fail
– Time un8l users return to mobile news stream
– …

10. Survival Analysis
• Interest is then in the survival func$on:
S(t) = P(Outcome > t) à probability of being alive a0er 8me t
= 1 – probability of dying before 8me t
S(t) = probability of not returning to stream aZer $me t
= 1 – probability of returning to stream before $me t
• Proper$es of S(t):
– S(0) = 1 à you are absolutely certain to be
alive at the beginning of $me.
– S(+∞) =0 à you will eventually die.
– S’(t) >= 0 à aZer one hour you cannot have
more chances to live than before.

11. Examples of a survival curve
higher post-click
engagement
lower post-click
engagement

12. Hazard and cumula$ve hazard
• Hazard func$on is defined as
rate of occurrence (users returning) at $me t
• Cumula$ve hazard (CHF) is the sum of the
risks (users returning) from dura$on 0 to t
• S(t) and H(t) are related as follows:
h(t) =
d
dt
log (S(t))
H(t) =
Z t
0
h(u)du
S(t) = e H(t)

13. Survival Random Forest
• How to es$mate S(t) from a
popula$on?
– Training data
• Survival Random Forest (SRF):
– Non-parametric
– High performance
– Learning in a mul$-threading
environment
• Is similar to “classic” Random
Forest but at leaf nodes you find
an es$mates of the Cumula8ve
Hazard H(t)

14. Experiments & dataset
• We sampled 46,914 observa$ons (impressions) from our na$ve ad log,
corresponding to:
– 2,438 ads
– Over 850 adver$sers.
• We perform a 80/20 training/test split.
• For each ad we extracted 42 features
• Hyper-parameters:
– 100 trees as we found it to op$mize the tradeoff $me vs generaliza$on
error
– Number of features sampled at each split is √nf, where nf is the number of
features.
• Offline Tests:
– AUC and ROC curves.
• Onine (A/B) Tests:
– Dwell $me upliZ, Bounce rate reduc$on, CTR upliZ.

15. Features (and their importance)
Historical features are most important
Then document object and readability features:
dwell $me is influenced by how much “actual” content is present
within a landing page, and what is the quality of this content.

16. Es$mated dwell $me
80% with dwell $me
≤ 100 seconds
median is 45 seconds
average is 65 seconds
Kaplan-Meier es$mate

17. ROC Curves SA achieve same
accuracy as
counterparts
Non-linear > linear
SRF > RF
SRF does not require
predetermined
threshold

18. UpliZ in online (A/B) tes$ng
Metrics
Dwell $me +13%
Bounce rate -10.3%
CTR +6.8%

19. Variable threshold?

20. Conclusions and future work
• Survival random forest based (slightly) outperforms all the
other compe$ng model and, more importantly, it allows to
compute the survival at different thresholds.
• The A/B test shows an improvement in user experience:
– A posi$ve effect on CTR
– A decrease in the number of bounces, and
– An increases in average dwell $me.
• Future work includes:
– Personaliza$on of threshold per user, per ads, and per ver$cal
(category)
– Integrate other signals related to revenue.

21. Appendix

22. Building $me and OOB error

23. Cumula$ve hazard func$on