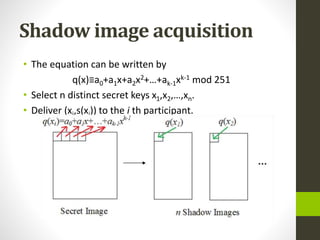
This document discusses image secret sharing, which is a technique to securely distribute a secret image among multiple participants. It describes Shamir's secret sharing algorithm, which divides a secret image into shadow images using polynomial interpolation. At least k shadow images are needed to reconstruct the original secret image. The document outlines the steps to generate and distribute shadow images and then recover the secret image. It also covers advantages like robustness and flexibility, disadvantages like potential information leakage, and applications like secure storage and password generation.

1. IMAGE SECRET
SHARING
Presented by : Nikita Kasar
Guided by : Dr. Sonali Patil

2. INTRODUCTION
• Secret sharing is a technique for protecting
sensitive data, such as cryptographic keys.
• Secret sharing is used in modern
cryptography to lower the risks associated
with compromised data.
• The first secret sharing schemes were
proposed by Shamir and Blakley in 1979.

3. PROBLEM STATEMENT
To provide security to images
using secret sharing algorithm.

4. OBJECTIVE
•To study different image secret
sharing algorithms.
• To secure data transmission in
networks which are used for
exchange of private images.

5. MOTIVATION
• If we do not process or hide
our secret information, the information
might be stolen by the hackers easily.
• The information is kept in a single
information-carrier. If the information-
carrier is lost or destroyed by an attacker,
the secret information might disappear.

6. WHY SECRET SHARING?

7. • Encryption – Single point failure.
• Decryption key may be lost.
• Encrypted content is corrupted during
transmission.
To address these reliability problems , an
image secret sharing scheme is good
alternative to remedy such vulnerabilities.

8. LITERATURE SURVEY
-------SHAMIR’S ALGORITHM------
• ● Based on polynomial interpolation
• ● It's (k, n) threshold scheme
• ● Dealer D distribute a secret s to n
players
• ● At least k participant's are required to
construct a secret s

9. THRESHOLD SCHEME
• Divide some data D into pieces/shadow
images D1,D2,……Dn in such a way that :
• i) Knowledge of any k or more Di pieces
makes D easily computable.
• Ii)Knowledge of any k-1 or fewer Di pieces
leaves D completely undetermined(in the
sense that all its possible values are
equally likely.)

10. Secret sharing in images
• Each pixel value of a secret image is a secret
message.
• We use the secret image to generate shadow
images and only require part of these shadow
images to reconstruct the secret image.
• The shadow images should not reveal any
information about the image.
• Ideally, each shadow image should look like
random noise so that anyone without the
permission won’t be able to get any information
about a secret image

11. Generation of Shadow
images

12. . Image sharing algorithm
(1) Suppress all pixels whose gray values greater than 250
to 250.
(2) Permute the pixels of the secret image to get a
permuted image, and pick up an integer threshold k.
(3) Sequentially take k not-shared-yet pixels of the
permuted image to form a (k-1)-degree polynomial.
q(x)≡a0+a1x+a2x2+…+ak-1xk-1 mod 251
where a0, a1, …, ak-1 are the k pixel values we take.
Then generate n pixel values q(r1),q(r2),…, q(rn) for n
shadow images, where 1 <= r1 <r2 <rn <= 250.
(4) Repeat step (3) until all pixels of the permuted image
are obtained.

13. Shadow image acquisition
• The equation can be written by
q(x)≡a0+a1x+a2x2+…+ak-1xk-1 mod 251
• Select n distinct secret keys x1,x2,…,xn.
• Deliver (xi,s(xi)) to the i th participant.

14. Revealing algorithm
(1) Collect at least k shadow images.
(2) Take the first unused pixel from each of k
shadow images.
(3) Use these k pixel values and Lagrange’s
polynomial interpolation to solve for the
coefficients a0, a1, …, ak-1. Put these
coefficients into the permuted image sequentially.
(4) Repeat steps (2) and (3) until all pixels of the k
shadow images processed.
(5) Inversely permute the pixels of the permuted
image to recover the original secret image.

15. Recovery of secret

16. ADVANTAGES
• The Shamir’s secret sharing scheme has a good
abstract foundation which provides an excellent
framework for proofs and applications.
• Shares can be easily added or removed without
affecting other shares.
• It is easy to change shares , keeping the same
secret.
• It is possible to provide more than 1 share per
individual.

17. DISADVANTAGE
• The Shamir-based method utilizes a scheme of
Lagrange polynomial interpolation to recover
the secret image from k out of n shadow image
generated from an original secret image.
• This method might expose some image features
in the shadow images without preprocessing the
secret image.

18. APPLICATIONS
• Medical applications such as tele diagnosis
require information exchange over insecure
networks.
• Password generation using shares.
• Generating shares by director of bank for the
bank’s vault unlocking code

19. APPLICATIONS
• ● Key Escrow/ Key Backup
• ● Used to build other cryptographic
primitives
• ● Secure multi party computation
• ● Electronic voting system

20. CONCLUSION& FUTURE SCOPE
- Share highly sensitive information
- Secret cannot be revealed with (k-1)
shares
- Secure storage
-Use of Watermarking
&Steganography

21. REFERENCES
• A. Shamir, “How to share a secret,” Communications of the
ACM, Vol. 22, No.11, 612613, 1979.
• C.C. Thien and J.C. Lin, “Secret image sharing,” Computer &
Graphics, Vol.26, No.1, 765-7710, 2002.
• “An Image Secret Sharing Method”,Li Bai Saroj Biswas ECE
Department Temple University Philadelphia, PA, U.S.A.
lbai@temple.edu
• A STUDY ON SECRET IMAGE SHARING
Ming-Hong Tsai1 and Chaur-Chin Chen2 1,2Department of
Computer Science, National Tsing Hua University, Hsinchu
30013, Taiwan 2Institute of Information Systems & Applications,
National Tsing Hua University, Hsinchu, Taiwan