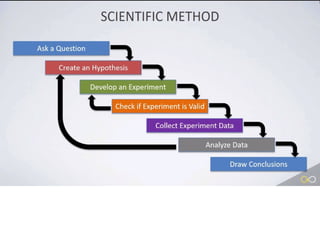
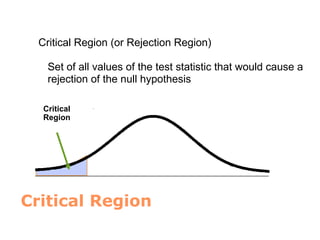
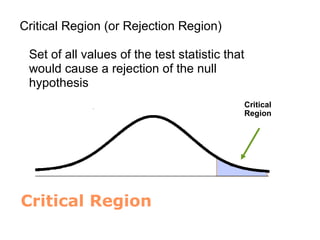
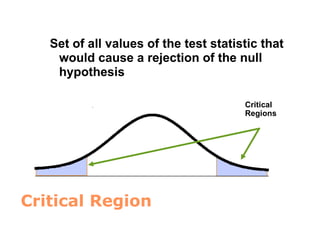
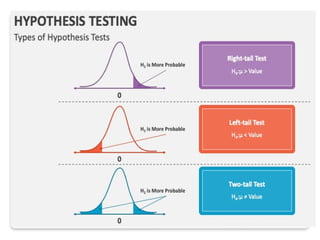
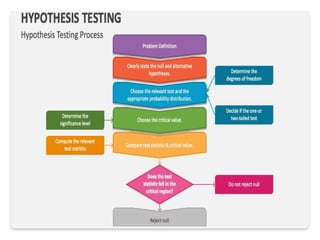
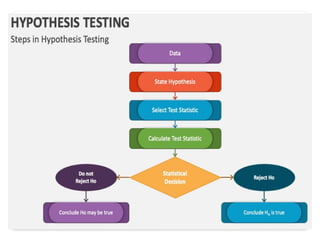
Hypothesis testing in statistics involves formulating a null hypothesis (H0) and an alternative hypothesis (H1) to assess claims about population properties. Critical concepts include the significance level, p-values, and test statistics, which help determine whether to reject the null hypothesis based on collected data. The document provides examples pertaining to various studies, highlighting the roles of H0 and H1 in evaluating differences or effects in research.