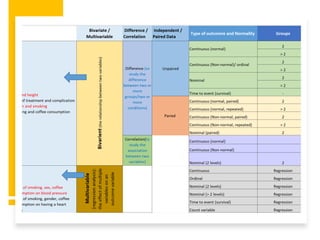
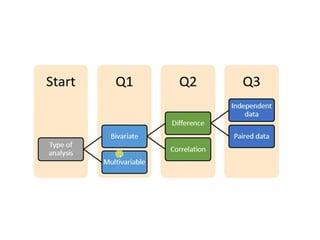
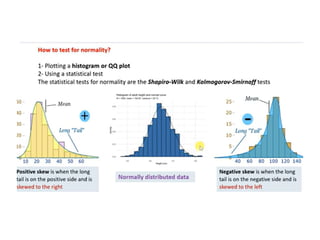
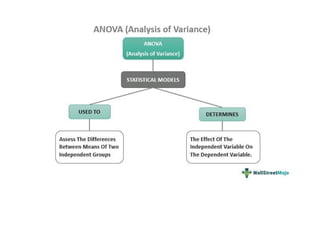
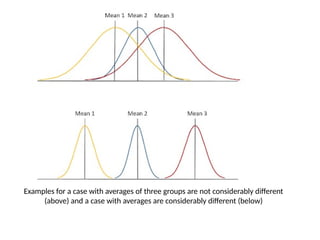
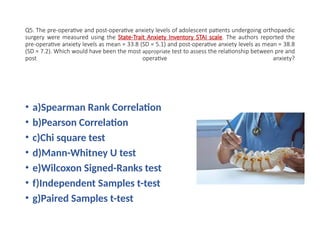
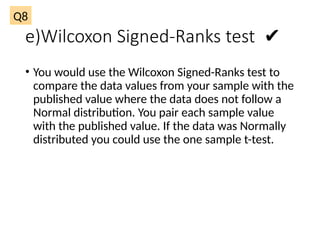
The document outlines various statistical techniques for analyzing independent and paired samples, including applications of ANOVA, Mann-Whitney U test, paired samples t-test, and correlations. It details how to choose appropriate tests based on the distribution of data and relationships between variables, specifically giving guidance on scenarios involving gestational age, anxiety levels, and nutritional supplements. Additionally, it explains the rationale behind using specific tests depending on whether the data is normally distributed or not.

1. Common Statistical
Techniques

3. • Independent/unpaired: The observations in each sample are
not related
• There is no relationship between the subjects in each sample.
• Subjects in the first group cannot also be in the second
group.
• No subject in either group can influence subjects in the
other group.
• Dependent/Paired: Paired samples include
• Pre-test/post-test samples (a variable is measured before and
after an intervention)
• When a variable is measured twice or more on the same
individual
• Cross-over trials
• Matched samples

4. • Cross-over trial: In a cross-over trial, each participant tries
both treatments, one after the other. For example, if we’re
testing two diets, each person would follow Diet A for a
while, then switch to Diet B (or vice versa). This way, each
person serves as their own comparison, which can make the
results more reliable.
• Matched samples: In matched samples, we pair up
participants based on similar characteristics, like age or
weight, and then give one person in each pair the treatment
and the other person a control or different treatment. This
helps make the comparison fairer because each pair is similar
in ways that might affect the outcome.

7. Q1. In a study, subjects are randomly assigned to one of three groups: control,
experimental A, or experimental B. After treatment, the mean scores for the three
groups are compared. The appropriate statistical test for comparing these means is:
• a)Spearman Rank Correlation
• b)Pearson Correlation
• c) the analysis of variance
• d)Mann-Whitney U test
• e)Wilcoxon Signed-Ranks test
• f)Independent Samples t-test
• g)Paired Samples t-test

8. c) the analysis of variance✔
• ANOVA is helpful for testing three or more
variables. It is similar to multiple two-sample t-
tests. However, it results in fewer type I errors and
is appropriate for a range of issues. ANOVA groups
differences by comparing the means of each group
and includes spreading out the variance into
diverse sources.
Q1

10. Examples for a case with averages of three groups are not considerably different
(above) and a case with averages are considerably different (below)

11. Q2. If we wished to test if there was a difference between the
gestational age of babies at birth and the use of a nutritional
supplement by their mothers during pregnancy which would
be the best test to choose?
• a)Spearman Rank Correlation
• b)Pearson Correlation
• c)Chi square test
• d)Mann-Whitney U test
• e)Wilcoxon Signed-Ranks test
• f)Independent Samples t-test
• g)Paired Samples t-test

12. d)Mann-Whitney U test ✔
• We have two independent groups defined by a
categorical and a continuous variable.
• The decision to be made is whether the continuous
variable is Normally distributed.
• Gestational age is likely to be negatively skewed because
pregnancies rarely go beyond 42 weeks.
• So a non-parametric test is required for independent
samples which is the Mann-Whitney U.
• If the data followed a Normal distribution or could be
transformed to follow one then an Independent
Samples t-test could be used.
Q2

13. Q3. The cotinine level was measured in women at the beginning
and end of their pregnancy. The change in cotinine was presented
on a Log scale. Which would be the best test to use to see if there
had been a change in cotinine level during pregnancy?
• a)Spearman Rank Correlation
• b)Pearson Correlation
• c)Chi square test
• d)Mann-Whitney U test
• e)Wilcoxon Signed-Ranks test
• f)Independent Samples t-test
• g)Paired Samples t-test
Nicotine Cotinine (Urine)

14. g)Paired Samples t-test ✔
• We have paired observations from the same
subject taken on different occasions.
• When data is presented on a Log scale it is usually
because the transformation results in the data
following a Normal distribution, so a parametric
test can be used. In this case the Paired Samples t-
test. A Mann-Whitney U test would be used when
the data does not follow a Normal distribution.
Q3

15. Q4. If we wished to estimate the strength of the linear relationship
between the weight of a mother and the weight of her baby at birth
which would be the best test to choose?
• a)Spearman Rank Correlation
• b)Pearson Correlation
• c)Chi square test
• d)Mann-Whitney U test
• e)Wilcoxon Signed-Ranks test
• f)Independent Samples t-test
• g)Paired Samples t-test

16. b)Pearson Correlation ✔
• Pearson Correlation estimates the strength of a
linear relationship.
• Linear Regression estimates the nature of the
relationship and assumes that one of the variables,
the independent variable can be used to predict the
nature of the dependent or outcome variable.
• If the relationship was not linear then Spearman
Rank Correlation could be used.
Q4

17. Q5. The pre-operative and post-operative anxiety levels of adolescent patients undergoing orthopaedic
surgery were measured using the State-Trait Anxiety Inventory STAI scale. The authors reported the
pre-operative anxiety levels as mean = 33.8 (SD = 5.1) and post-operative anxiety levels as mean = 38.8
(SD = 7.2). Which would have been the most appropriate test to assess the relationship between pre and
post operative anxiety?
• a)Spearman Rank Correlation
• b)Pearson Correlation
• c)Chi square test
• d)Mann-Whitney U test
• e)Wilcoxon Signed-Ranks test
• f)Independent Samples t-test
• g)Paired Samples t-test

18. g)Paired Samples t-test ✔
• We have paired data from the same subjects so a
Paired Samples t-test is appropriate assuming the
differences in the data followed a Normal
distribution which is implied by the presentation of
the means and standard deviations.
• The authors of this study did not present the mean
difference of the pre - post values which should be
quoted together with 95% confidence intervals.
Q5

19. Q6. Which test would you choose to compare
two groups with skewed unpaired continuous
data?
• a)Spearman Rank Correlation
• b)Pearson Correlation
• c)Chi square test
• d)Mann-Whitney U test
• e)Wilcoxon Signed-Ranks test
• f)Independent Samples t-test
• g)Paired Samples t-test

20. d)Mann-Whitney U test ✔
Q6

21. Q7. Which test would you choose to compare
the relationship between two continuous
variables which had skewed distributions?
• a)Spearman Rank Correlation
• b)Pearson Correlation
• c)Chi square test
• d)Mann-Whitney U test
• e)Wilcoxon Signed-Ranks test
• f)Independent Samples t-test
• g)Paired Samples t-test

22. a)Spearman Rank Correlation ✔
• The Spearman Rank Correlation coefficient is used.
• Pearson correlation assumes that at least one of
the variables follows a Normal distribution.
Q7

23. Q8. Which test would you choose to compare a single sample
of non-parametric values with a published value?
• a)Spearman Rank Correlation
• b)Pearson Correlation
• c)Chi square test
• d)Mann-Whitney U test
• e)Wilcoxon Signed-Ranks test
• f)Independent Samples t-test
• g)Paired Samples t-test

24. e)Wilcoxon Signed-Ranks test ✔
• You would use the Wilcoxon Signed-Ranks test to
compare the data values from your sample with the
published value where the data does not follow a
Normal distribution. You pair each sample value
with the published value. If the data was Normally
distributed you could use the one sample t-test.
Q8