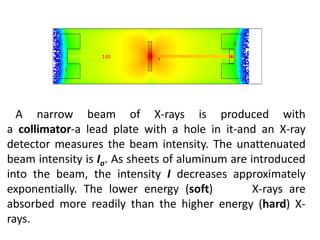
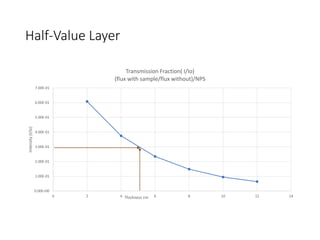
X-rays are absorbed differently by different materials. Heavy elements like calcium absorb X-rays much more than light elements like carbon and hydrogen. This is why bones stand out clearly on X-rays, while soft tissues like fat, muscle and tumors are difficult to distinguish as they absorb X-rays equally. The intensity of an X-ray beam decreases exponentially as it passes through materials due to absorption and scattering of photons. The thickness of material needed to reduce an X-ray beam's intensity by half is known as the half-value layer, which depends on the linear attenuation coefficient of the material.

1. How X-rays are absorbed
X-rays are not absorbed equally well by all materials; if they were,
they would not be very useful in diagnosis. Heavy elements such as
calcium are much better absorbers of X-rays than light elements such
as carbon, oxygen, and hydrogen, and as a result, structures
containing heavy elements, like the bones, stand out clearly. The soft
tissues-fat, muscles, and tumors-all absorb about equally well and are
thus difficult to distinguish from each other on an X-ray image .
The attenuation of an X-ray beam is its reduction due to the
absorption and scattering of some of the photons out of the beam. A
simple method of measuring the attenuation of an X-ray beam is
shown below.

2. A narrow beam of X-rays is produced with
a collimator-a lead plate with a hole in it-and an X-ray
detector measures the beam intensity. The unattenuated
beam intensity is Io. As sheets of aluminum are introduced
into the beam, the intensity I decreases approximately
exponentially. The lower energy (soft) X-rays are
absorbed more readily than the higher energy (hard) X-
rays.

3. The intensity of a monoenergetic X-ray beam would decrease
exponentially. The exponential equation describing the attenuation
curve for a monoenergetic X-ray beam is: -
Where e=2.718, x is the thickness of the attenuator, and μ is the
linear attenuation coefficient of the attenuator. The linear
attenuation coefficient is dependent on the energy of the X-ray
photons; as the beam becomes harder, it decreases.
The half-value layer (HVL) for an X-ray beam is the thickness of a
given material that will reduce the beam intensity by one-half.


 e
I
I o

4. Half-Value Layer
0.00E+00
1.00E-01
2.00E-01
3.00E-01
4.00E-01
5.00E-01
6.00E-01
7.00E-01
0 2 4 6 8 10 12 14
Intensity
(I/Io)
Thickness cm
Transmission Fraction( I/Io)
(flux with sample/flux without)/NPS

5. For a monenergetic X-ray beam, the second half-value
layer equals the first half-value layer. The half-value layer is
related to the linear attenuation coefficient by: -
The mass attenuation coefficient μm is used to remove the
effect of density when comparing attenuation in several
materials. The mass attenuation coefficient of a material is
equal to the linear attenuation coefficient μ divided by the
density ρ of the materials.
The quantity ρx is in grams per square centimeter and is
sometimes called the area density; μm is in square
centimeters per gram.

693
.
0

HVL
I=Ioe –(μ/ρ)(ρx)=Ioe–μm(ρx)