Downloaded 61 times
Uploaded byJunya Tanaka
Inference in First-Order Logic 2
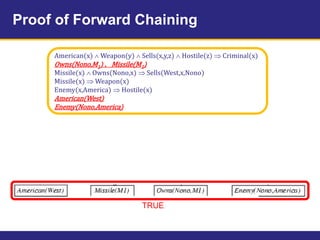
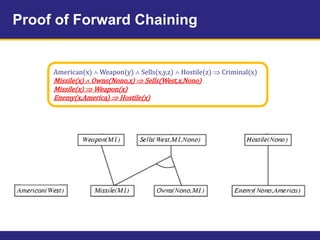
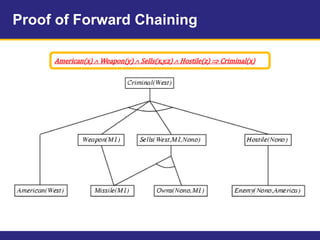
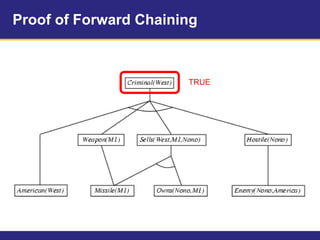
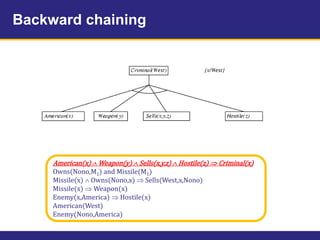
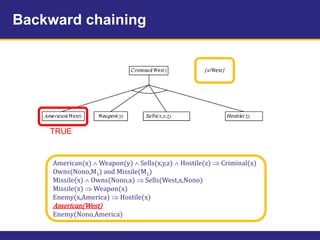
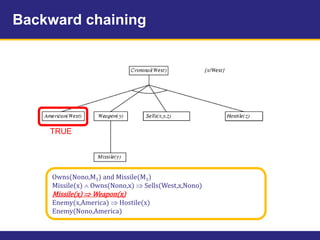
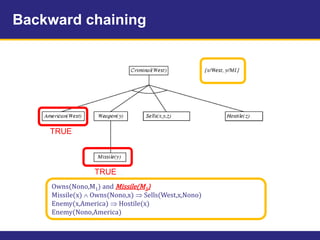
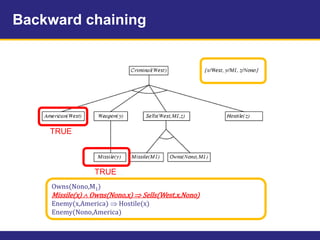
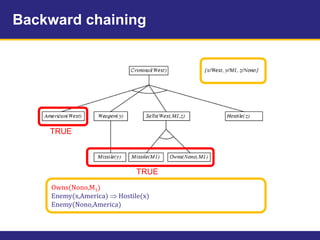
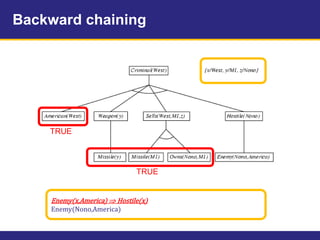
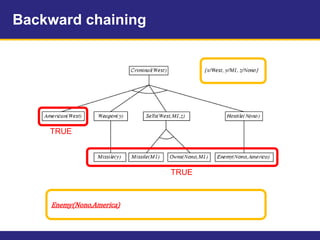
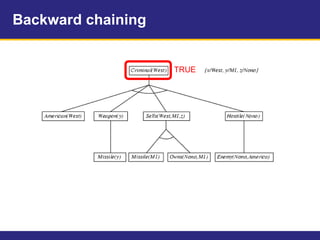
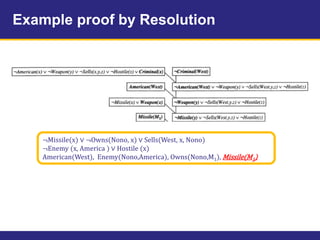
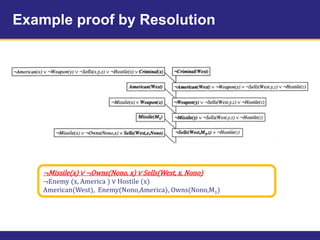
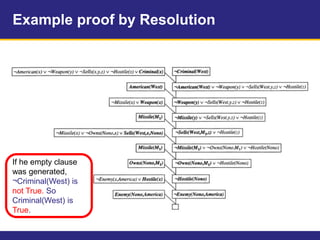
The document provides an example knowledge base to demonstrate forward chaining, backward chaining, and resolution. The knowledge base describes facts about a scenario where an American, Colonel West, sold missiles to the hostile nation of Nono. Forward chaining and backward chaining are used to prove that West is a criminal from these facts. Resolution converts the knowledge base and query to conjunctive normal form and derives the empty clause, proving the query.
More Related Content
Similar to Inference in First-Order Logic 2
![Polymer [ बहुलक ] Chemistry Notes PDF - Irfanullah Mehar - JJ Sir Chemistry.pdf](https://cdn.slidesharecdn.com/ss_thumbnails/polymerchemistrynotespdf-irfanullahmehar-jjsirchemistry-260210172118-3f9b37f7-thumbnail.jpg?width=640&height=640&fit=bounds)
![ANIMAL_CELL_,_TISSUE_AND_ORGAN_CULTURE[1].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/animalcelltissueandorganculture1-260204172026-4462b440-thumbnail.jpg?width=640&height=640&fit=bounds)
Inference in First-Order Logic 2
- 1. Example for ForwardChaining, Backward Chaining and Resolution Artificial Intelligence, A Modern Approach, CH.9 2017.05.12(Thu) Junya Tanaka (M1)
- 2. Introduction • Chapter 9examine effective procedures for answering questions posed in first-order logic • Suppose same example for three important methods of inference(forward Chaining, Backward Chaining and Resolution)
- 3. Example(1/3) • Consider thefollowing problem: The law says that it is a crime for an American to sell weapons to hostile nations. The country Nono, an enemy of America, has some missiles, and all of its missiles were sold to it by Colonel West, who is American • Prove oWest is a criminal
- 4. Example(2/3) • Represent thesefacts as first-order definite clauses • it is a crime for an American to sell weapons to hostile nations: American(x) Weapon(y) Sells(x,y,z) Hostile(z) Criminal(x) • Nono … has some missiles, i.e., x Owns(Nono,x) Missile(x): Owns(Nono,M1) and Missile(M1) • … all of its missiles were sold to it by Colonel West Missile(x) Owns(Nono,x) Sells(West,x,Nono) • Missiles are weapons: Missile(x) Weapon(x) • An enemy of America counts as "hostile“: Enemy(x,America) Hostile(x) • West, who is American … American(West) • The country Nono, an enemy of America … Enemy(Nono,America)
- 5. Example(1/3) • Represent thesefacts as first-order definite clauses The law says that it is a crime for an American to sell weapons to hostile nations. The country Nono, an enemy of America, has some missiles, and all of its missiles were sold to it by Colonel West, who is American American(x) Weapon(y) Sells(x,y,z) Hostile(z) Criminal(x) Owns(Nono,M1) ，Missile(M1) Missile(x) Owns(Nono,x) Sells(West,x,Nono) Missile(x) Weapon(x) Enemy(x,America) Hostile(x) American(West) Enemy(Nono,America) Knowledge Base
- 6. Forward Chaining • Idea: oStartwith atomic sentences in the KB oApply Modus Ponens Add new atomic sentences until no further inferences can be made • Works well for a KB consisting of Situation Response clauses when processing newly arrived data
- 7. Proof of ForwardChaining American(x) Weapon(y) Sells(x,y,z) Hostile(z) Criminal(x) Owns(Nono,M1) ，Missile(M1) Missile(x) Owns(Nono,x) Sells(West,x,Nono) Missile(x) Weapon(x) Enemy(x,America) Hostile(x) American(West) Enemy(Nono,America) TRUE
- 8. Proof of ForwardChaining American(x) Weapon(y) Sells(x,y,z) Hostile(z) Criminal(x) Missile(x) Owns(Nono,x) Sells(West,x,Nono) Missile(x) Weapon(x) Enemy(x,America) Hostile(x)
- 9. Proof of ForwardChaining American(x) Weapon(y) Sells(x,y,z) Hostile(z) Criminal(x)
- 10. Proof of ForwardChaining TRUE
- 11. Backward Chaining • BackwardChaining is a “generator” oGenerates all possible substitutions to the goal. • Backward Chaining is depth-first. • Idea oStarts from the goal oMatches each literal in goal’s premise from left to right with facts in Knowledge Base oCreates new recursive call, if the call succeed, the proof in that branch is completed. oIf the current goal is completed, continue with new sentence that can lead to goal. Be reminded : goal might be able to reached from one or more rules.
- 12. Backward chaining American(x) Weapon(y) Sells(x,y,z) Hostile(z) Criminal(x) Owns(Nono,M1) and Missile(M1) Missile(x) Owns(Nono,x) Sells(West,x,Nono) Missile(x) Weapon(x) Enemy(x,America) Hostile(x) American(West) Enemy(Nono,America)
- 13. Backward chaining American(x) Weapon(y) Sells(x,y,z) Hostile(z) Criminal(x) Owns(Nono,M1) and Missile(M1) Missile(x) Owns(Nono,x) Sells(West,x,Nono) Missile(x) Weapon(x) Enemy(x,America) Hostile(x) American(West) Enemy(Nono,America)
- 14. Backward chaining American(x) Weapon(y) Sells(x,y,z) Hostile(z) Criminal(x) Owns(Nono,M1) and Missile(M1) Missile(x) Owns(Nono,x) Sells(West,x,Nono) Missile(x) Weapon(x) Enemy(x,America) Hostile(x) American(West) Enemy(Nono,America) TRUE
- 15. Backward chaining Owns(Nono,M1) andMissile(M1) Missile(x) Owns(Nono,x) Sells(West,x,Nono) Missile(x) Weapon(x) Enemy(x,America) Hostile(x) Enemy(Nono,America) TRUE
- 16. Backward chaining Owns(Nono,M1) andMissile(M1) Missile(x) Owns(Nono,x) Sells(West,x,Nono) Enemy(x,America) Hostile(x) Enemy(Nono,America) TRUE TRUE
- 17. Backward chaining Owns(Nono,M1) Missile(x) Owns(Nono,x) Sells(West,x,Nono) Enemy(x,America) Hostile(x) Enemy(Nono,America) TRUE TRUE
- 18. Backward chaining Owns(Nono,M1) Enemy(x,America) Hostile(x) Enemy(Nono,America) TRUE TRUE
- 19. Backward chaining Enemy(x,America) Hostile(x) Enemy(Nono,America) TRUE TRUE
- 20.
- 21.
- 22. Resolution • CNF(Conjunctive NormalForm) for First-order logic oEvery FOL sentence can be converted into an inferentially equivalent CNF sentences oAs in propositional logic, resolution algorithm works with sentences in CNF • Proof of Resolution oMake sure KB and query(namely a) are in CNF form. oApply resolution steps to CNF(KB ∧ ¬a) We include ¬a in order to proof by contradiction. oApply resolution until empty clause appears
- 23. Example proof byResolution • The example sentences in CNF American(x) Weapon(y) Sells(x,y,z) Hostile(z) Criminal(x) Missile(x) Owns(Nono,x) Sells(West,x,Nono) Missile(x) Weapon(x) Enemy(x,America) Hostile(x) American(West), Enemy(Nono,America), Owns(Nono,M1), Missile(M1) ¬American(x) ∨ ¬Weapon(y) ∨ ¬Sells(x, y, z) ∨ ¬Hostile(z) ∨ Criminal(x) ¬Missile(x) ∨ ¬Owns(Nono, x) ∨ Sells(West, x, Nono) ¬Missile(x) ∨ Weapon(x) ¬Enemy (x, America ) ∨ Hostile (x) American(West), Enemy(Nono,America), Owns(Nono,M1), Missile(M1) ¬Criminal(West)
- 24. Example proof byResolution ¬American(x) ∨ ¬Weapon(y) ∨ ¬Sells(x, y, z) ∨ ¬Hostile(z) ∨ Criminal(x) ¬Missile(x) ∨ ¬Owns(Nono, x) ∨ Sells(West, x, Nono) ¬Missile(x) ∨ Weapon(x) ¬Enemy (x, America ) ∨ Hostile (x) American(West), Enemy(Nono,America), Owns(Nono,M1), Missile(M1) ¬Criminal(West)
- 25. Example proof byResolution ¬Missile(x) ∨ ¬Owns(Nono, x) ∨ Sells(West, x, Nono) ¬Missile(x) ∨ Weapon(x) ¬Enemy (x, America ) ∨ Hostile (x) American(West), Enemy(Nono,America), Owns(Nono,M1), Missile(M1)
- 26. Example proof byResolution ¬Missile(x) ∨ ¬Owns(Nono, x) ∨ Sells(West, x, Nono) ¬Missile(x) ∨ Weapon(x) ¬Enemy (x, America ) ∨ Hostile (x) American(West), Enemy(Nono,America), Owns(Nono,M1), Missile(M1)
- 27. Example proof byResolution ¬Missile(x) ∨ ¬Owns(Nono, x) ∨ Sells(West, x, Nono) ¬Missile(x) ∨ Weapon(x) ¬Enemy (x, America ) ∨ Hostile (x) Enemy(Nono,America), Owns(Nono,M1), Missile(M1)
- 28. Example proof byResolution ¬Missile(x) ∨ ¬Owns(Nono, x) ∨ Sells(West, x, Nono) ¬Enemy (x, America ) ∨ Hostile (x) American(West), Enemy(Nono,America), Owns(Nono,M1), Missile(M1)
- 29. Example proof byResolution ¬Missile(x) ∨ ¬Owns(Nono, x) ∨ Sells(West, x, Nono) ¬Enemy (x, America ) ∨ Hostile (x) American(West), Enemy(Nono,America), Owns(Nono,M1)
- 30. Example proof byResolution If he empty clause was generated, ¬Criminal(West) is not True. So Criminal(West) is True.
Editor's Notes
- #8 The proof tree generated by forward chaining on the crime example. The initial facts appear at the bottom level, facts inferred on the first iteration in the middle level, and facts inferred on the second iteration at the top level.
- #9 The proof tree generated by forward chaining on the crime example. The initial facts appear at the bottom level, facts inferred on the first iteration in the middle level, and facts inferred on the second iteration at the top level.
- #10 The proof tree generated by forward chaining on the crime example. The initial facts appear at the bottom level, facts inferred on the first iteration in the middle level, and facts inferred on the second iteration at the top level.
- #11 The proof tree generated by forward chaining on the crime example. The initial facts appear at the bottom level, facts inferred on the first iteration in the middle level, and facts inferred on the second iteration at the top level.
- #13 Proof tree constructed by backward chaining to prove that West is a criminal. The tree should be read depth first, left to right. To prove Criminal (West ), we have to prove the four conjuncts below it. Some of these are in the knowledge base, and others require further backward chaining. Bindings for each successful unification are shown next to the corresponding subgoal. Note that once one subgoal in a conjunction succeeds, its substitution is applied to subsequent subgoals. Thus, by the time FOL-BC-ASK gets to the last conjunct, originally Hostile(z), z is already bound to Nono.
- #14 Proof tree constructed by backward chaining to prove that West is a criminal. The tree should be read depth first, left to right. To prove Criminal (West ), we have to prove the four conjuncts below it. Some of these are in the knowledge base, and others require further backward chaining. Bindings for each successful unification are shown next to the corresponding subgoal. Note that once one subgoal in a conjunction succeeds, its substitution is applied to subsequent subgoals. Thus, by the time FOL-BC-ASK gets to the last conjunct, originally Hostile(z), z is already bound to Nono.
- #15 Proof tree constructed by backward chaining to prove that West is a criminal. The tree should be read depth first, left to right. To prove Criminal (West ), we have to prove the four conjuncts below it. Some of these are in the knowledge base, and others require further backward chaining. Bindings for each successful unification are shown next to the corresponding subgoal. Note that once one subgoal in a conjunction succeeds, its substitution is applied to subsequent subgoals. Thus, by the time FOL-BC-ASK gets to the last conjunct, originally Hostile(z), z is already bound to Nono.
- #16 Proof tree constructed by backward chaining to prove that West is a criminal. The tree should be read depth first, left to right. To prove Criminal (West ), we have to prove the four conjuncts below it. Some of these are in the knowledge base, and others require further backward chaining. Bindings for each successful unification are shown next to the corresponding subgoal. Note that once one subgoal in a conjunction succeeds, its substitution is applied to subsequent subgoals. Thus, by the time FOL-BC-ASK gets to the last conjunct, originally Hostile(z), z is already bound to Nono.
- #17 Proof tree constructed by backward chaining to prove that West is a criminal. The tree should be read depth first, left to right. To prove Criminal (West ), we have to prove the four conjuncts below it. Some of these are in the knowledge base, and others require further backward chaining. Bindings for each successful unification are shown next to the corresponding subgoal. Note that once one subgoal in a conjunction succeeds, its substitution is applied to subsequent subgoals. Thus, by the time FOL-BC-ASK gets to the last conjunct, originally Hostile(z), z is already bound to Nono.
- #18 Proof tree constructed by backward chaining to prove that West is a criminal. The tree should be read depth first, left to right. To prove Criminal (West ), we have to prove the four conjuncts below it. Some of these are in the knowledge base, and others require further backward chaining. Bindings for each successful unification are shown next to the corresponding subgoal. Note that once one subgoal in a conjunction succeeds, its substitution is applied to subsequent subgoals. Thus, by the time FOL-BC-ASK gets to the last conjunct, originally Hostile(z), z is already bound to Nono.
- #19 Proof tree constructed by backward chaining to prove that West is a criminal. The tree should be read depth first, left to right. To prove Criminal (West ), we have to prove the four conjuncts below it. Some of these are in the knowledge base, and others require further backward chaining. Bindings for each successful unification are shown next to the corresponding subgoal. Note that once one subgoal in a conjunction succeeds, its substitution is applied to subsequent subgoals. Thus, by the time FOL-BC-ASK gets to the last conjunct, originally Hostile(z), z is already bound to Nono.
- #20 Proof tree constructed by backward chaining to prove that West is a criminal. The tree should be read depth first, left to right. To prove Criminal (West ), we have to prove the four conjuncts below it. Some of these are in the knowledge base, and others require further backward chaining. Bindings for each successful unification are shown next to the corresponding subgoal. Note that once one subgoal in a conjunction succeeds, its substitution is applied to subsequent subgoals. Thus, by the time FOL-BC-ASK gets to the last conjunct, originally Hostile(z), z is already bound to Nono.
- #21 Proof tree constructed by backward chaining to prove that West is a criminal. The tree should be read depth first, left to right. To prove Criminal (West ), we have to prove the four conjuncts below it. Some of these are in the knowledge base, and others require further backward chaining. Bindings for each successful unification are shown next to the corresponding subgoal. Note that once one subgoal in a conjunction succeeds, its substitution is applied to subsequent subgoals. Thus, by the time FOL-BC-ASK gets to the last conjunct, originally Hostile(z), z is already bound to Nono.
- #22 Proof tree constructed by backward chaining to prove that West is a criminal. The tree should be read depth first, left to right. To prove Criminal (West ), we have to prove the four conjuncts below it. Some of these are in the knowledge base, and others require further backward chaining. Bindings for each successful unification are shown next to the corresponding subgoal. Note that once one subgoal in a conjunction succeeds, its substitution is applied to subsequent subgoals. Thus, by the time FOL-BC-ASK gets to the last conjunct, originally Hostile(z), z is already bound to Nono.