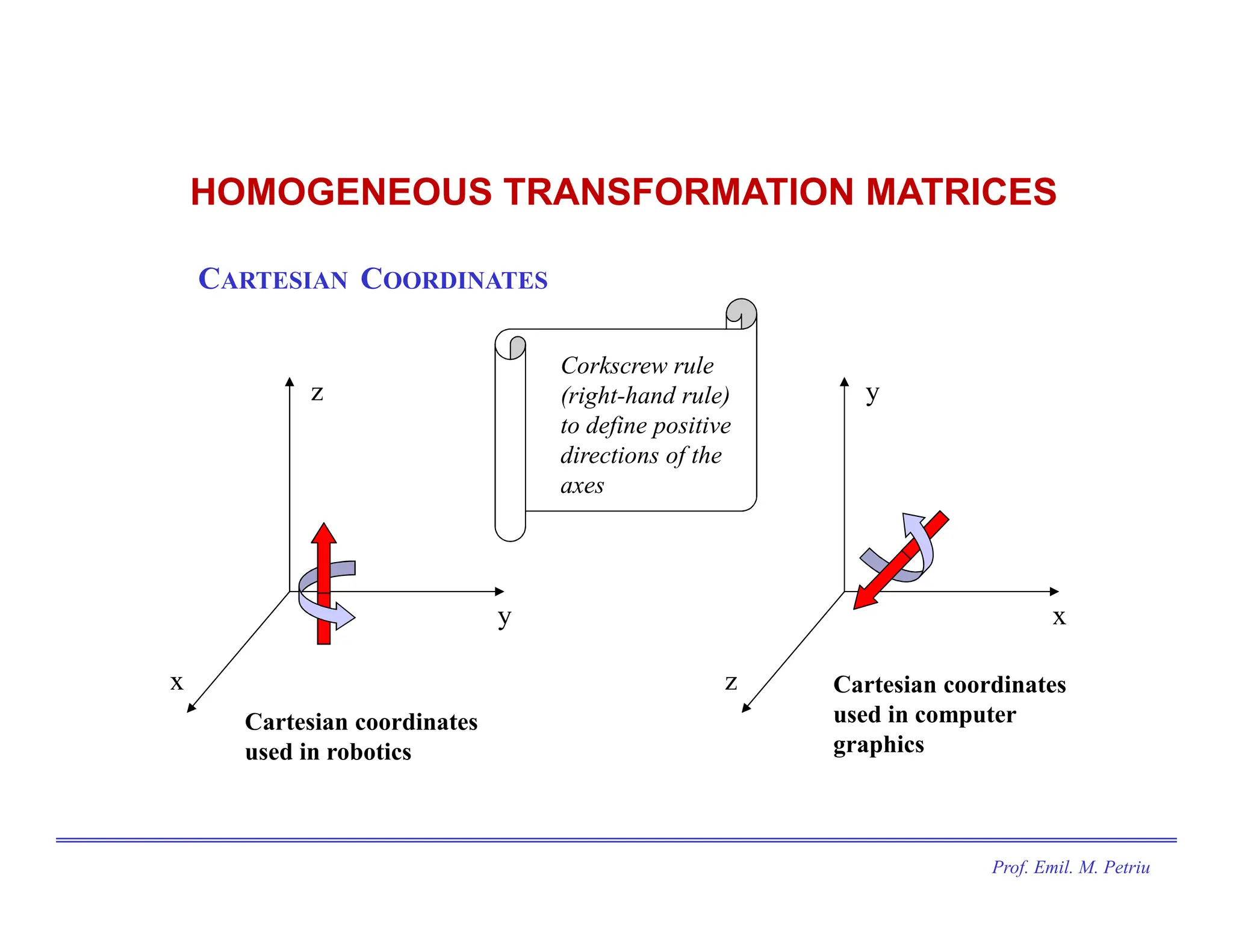
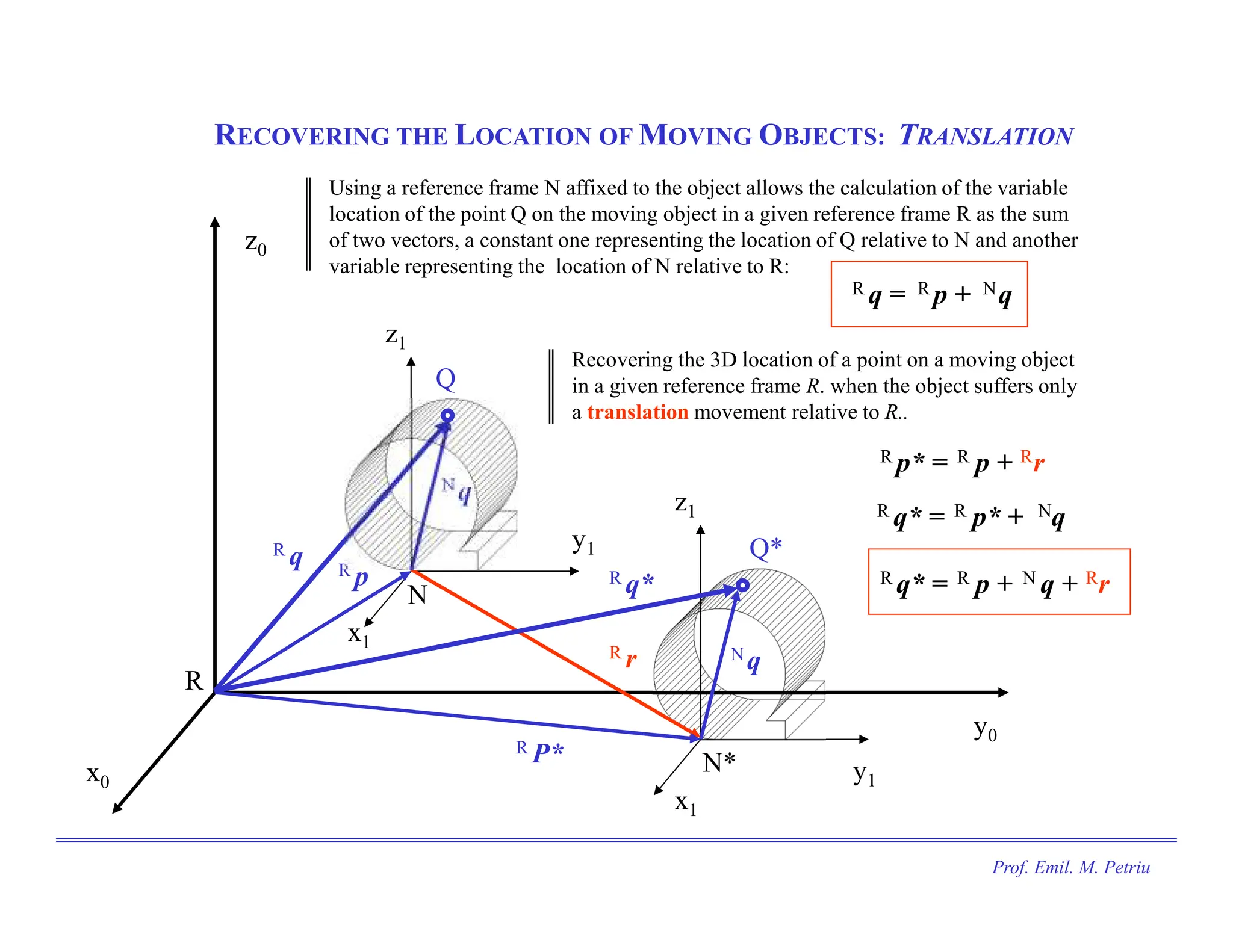
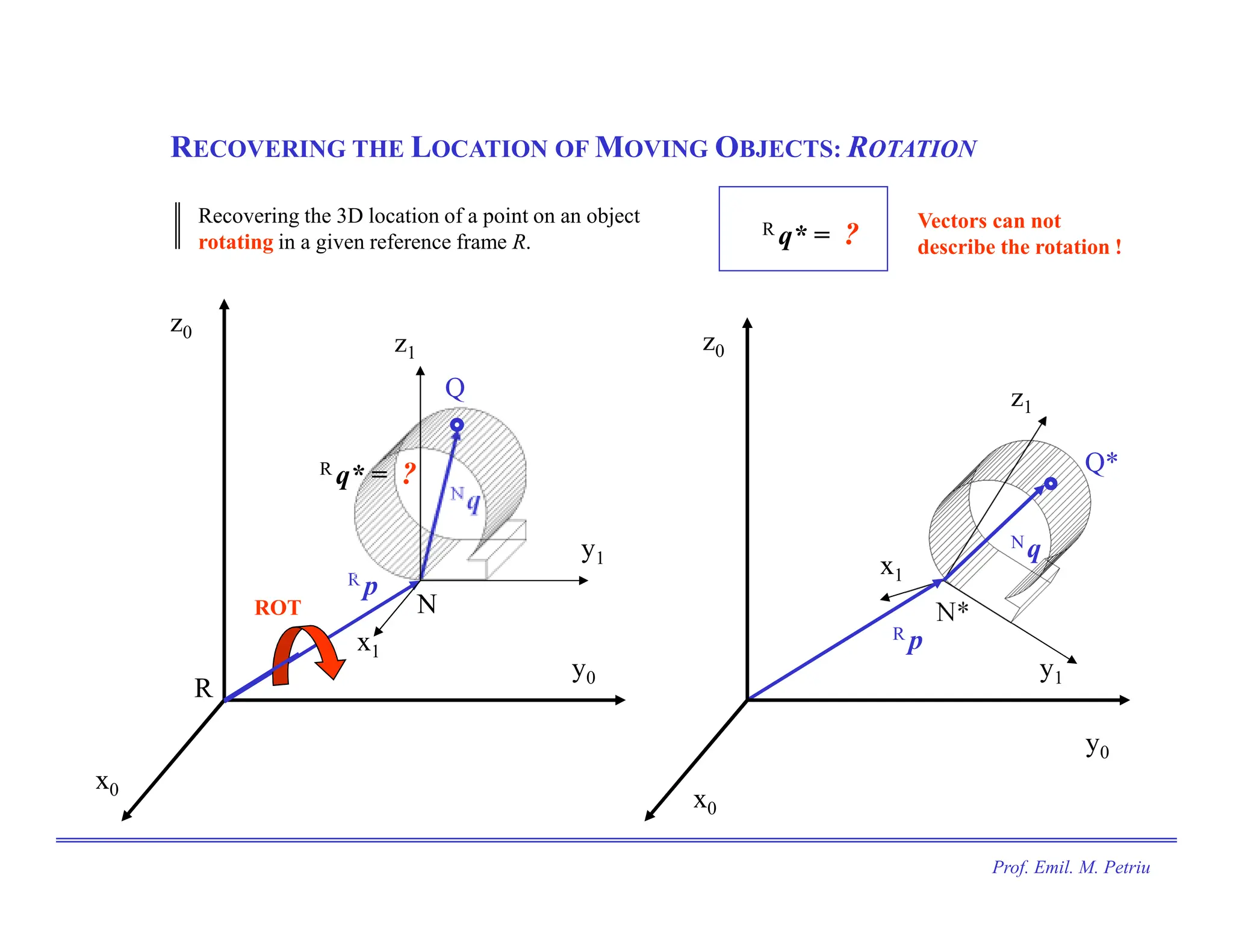
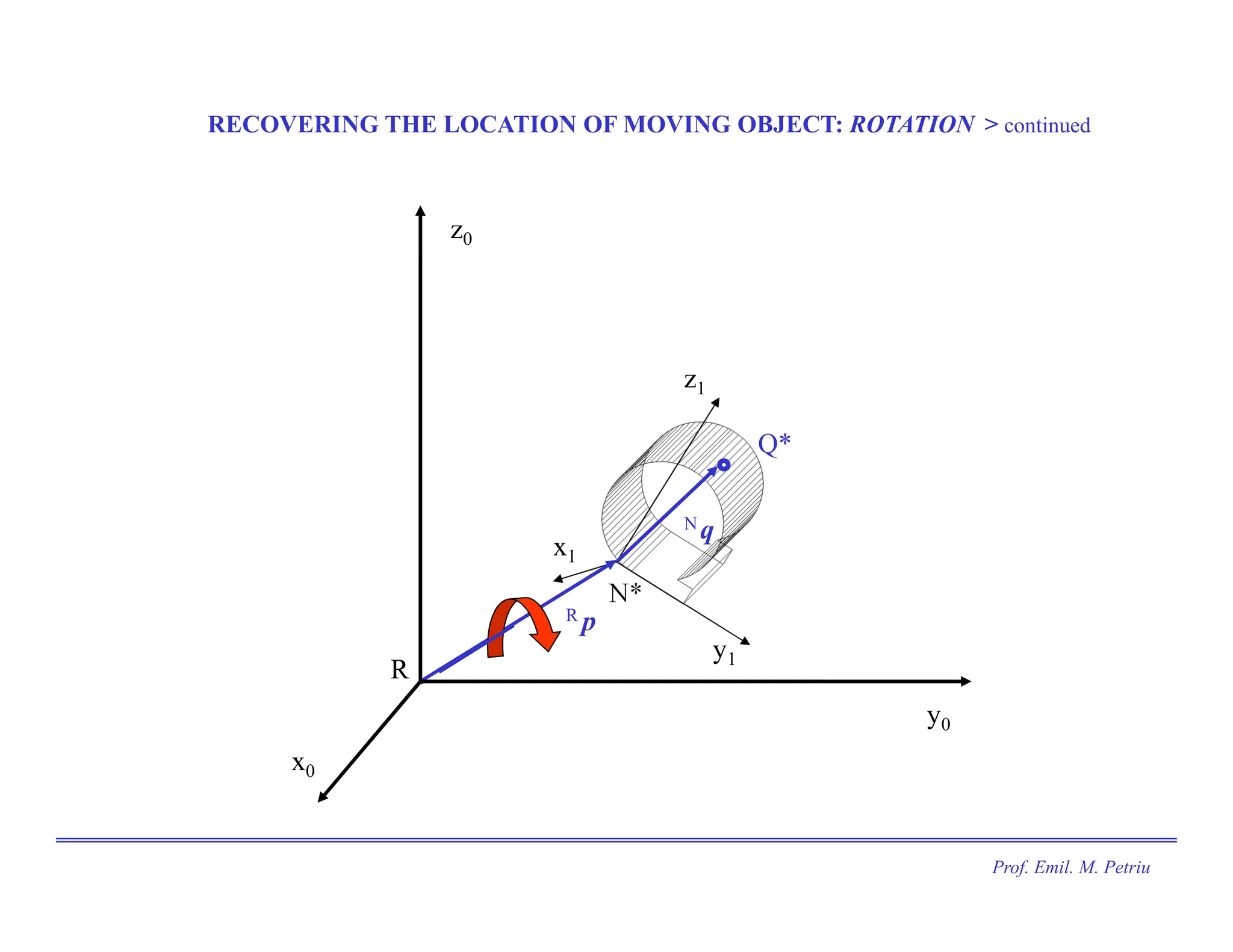
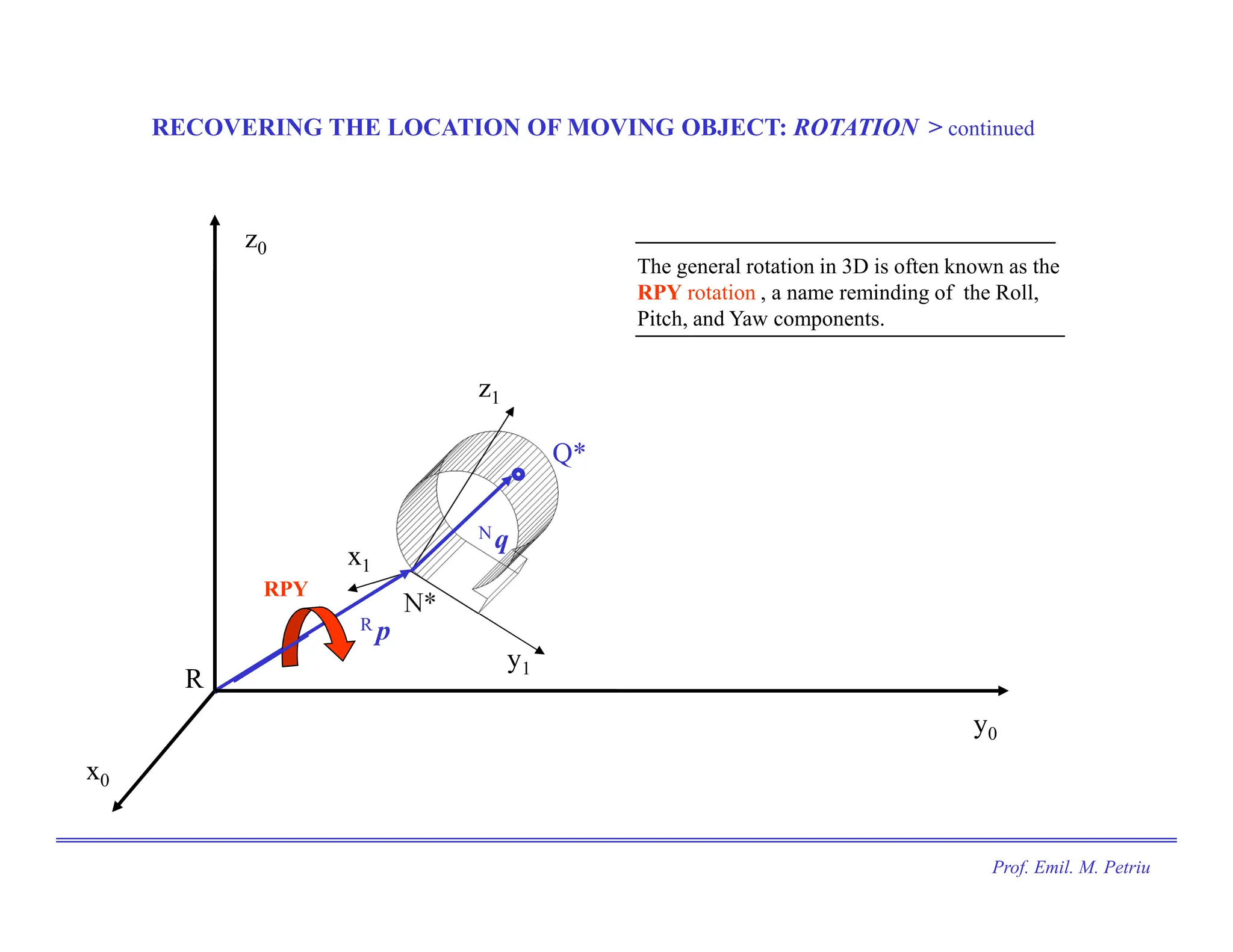
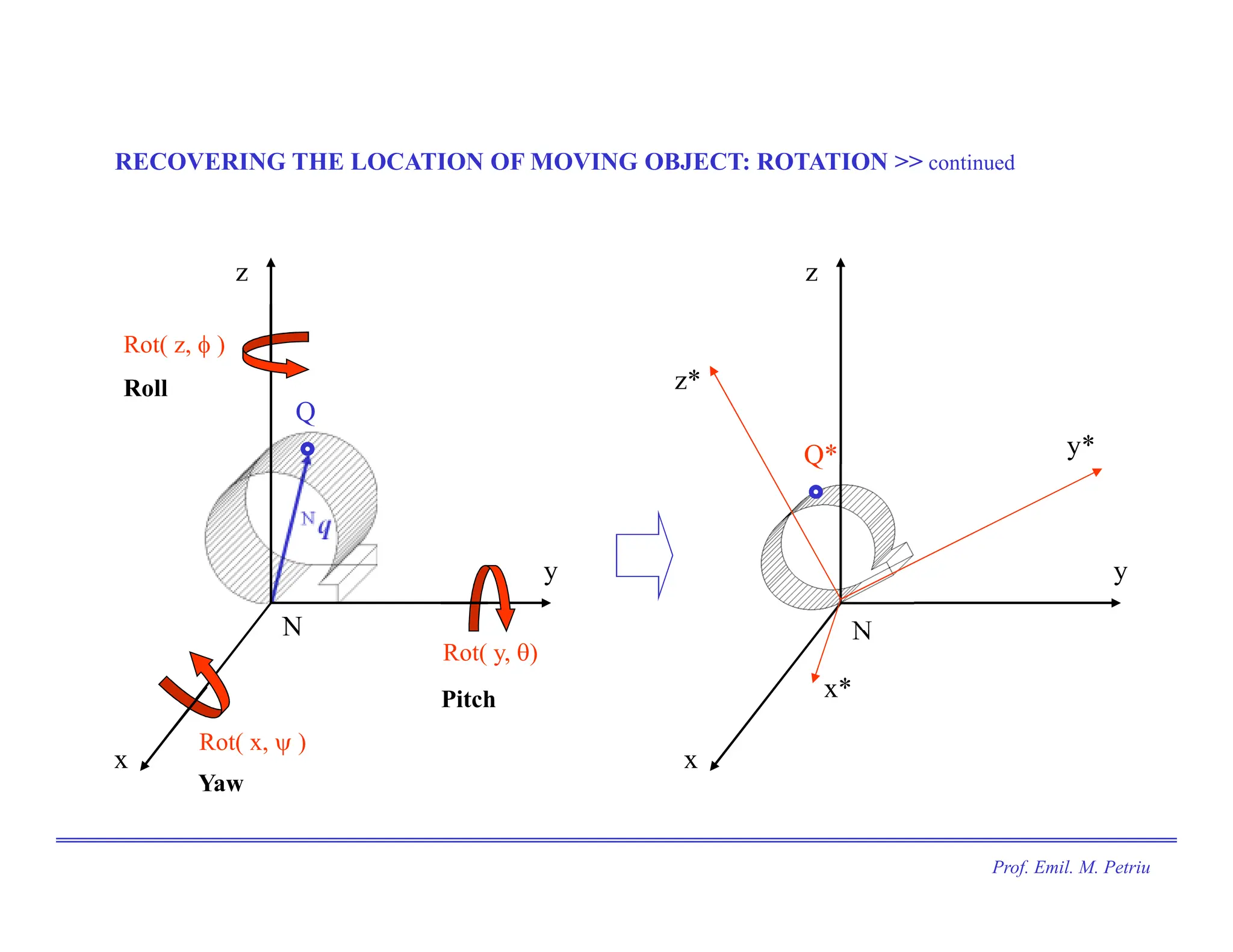
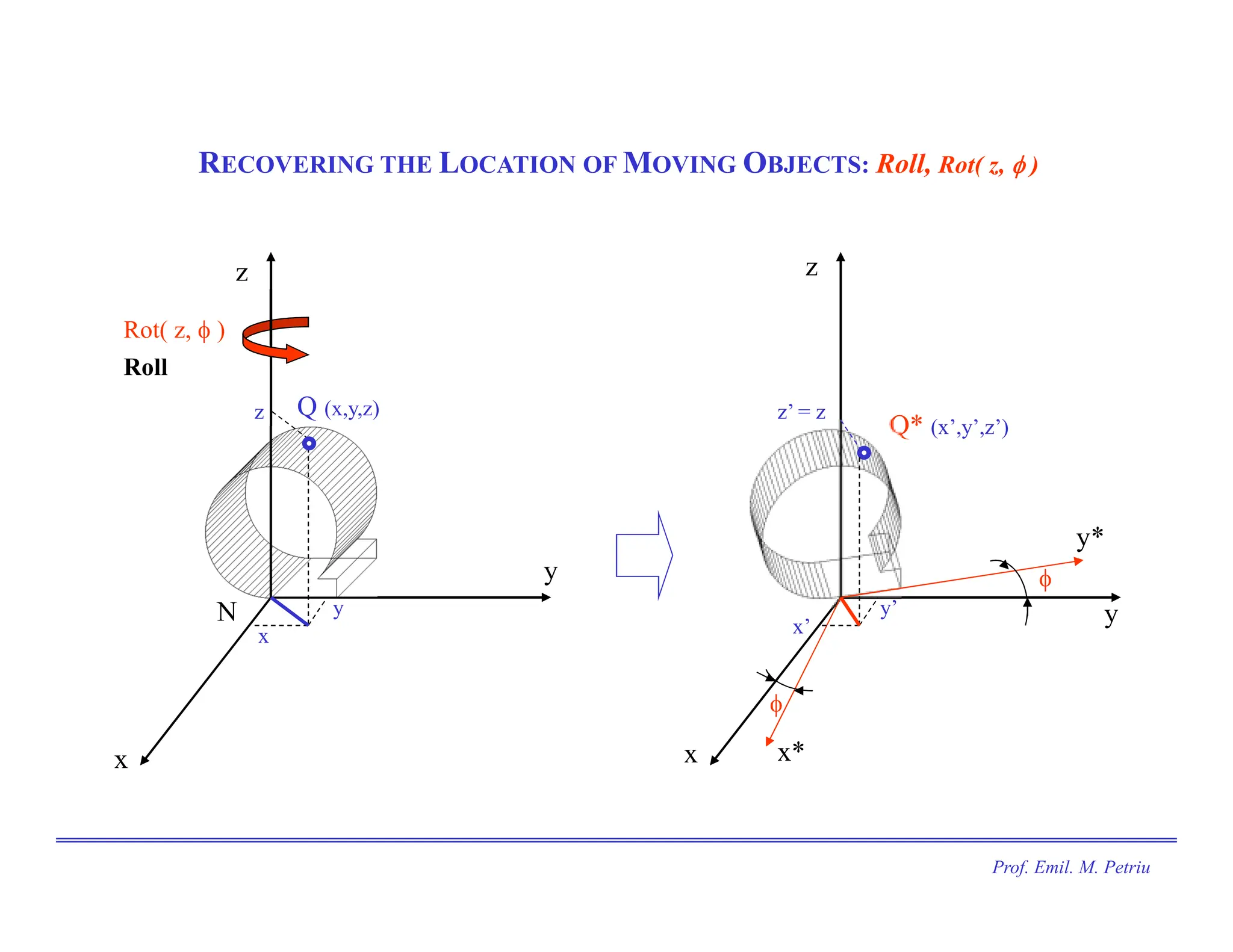
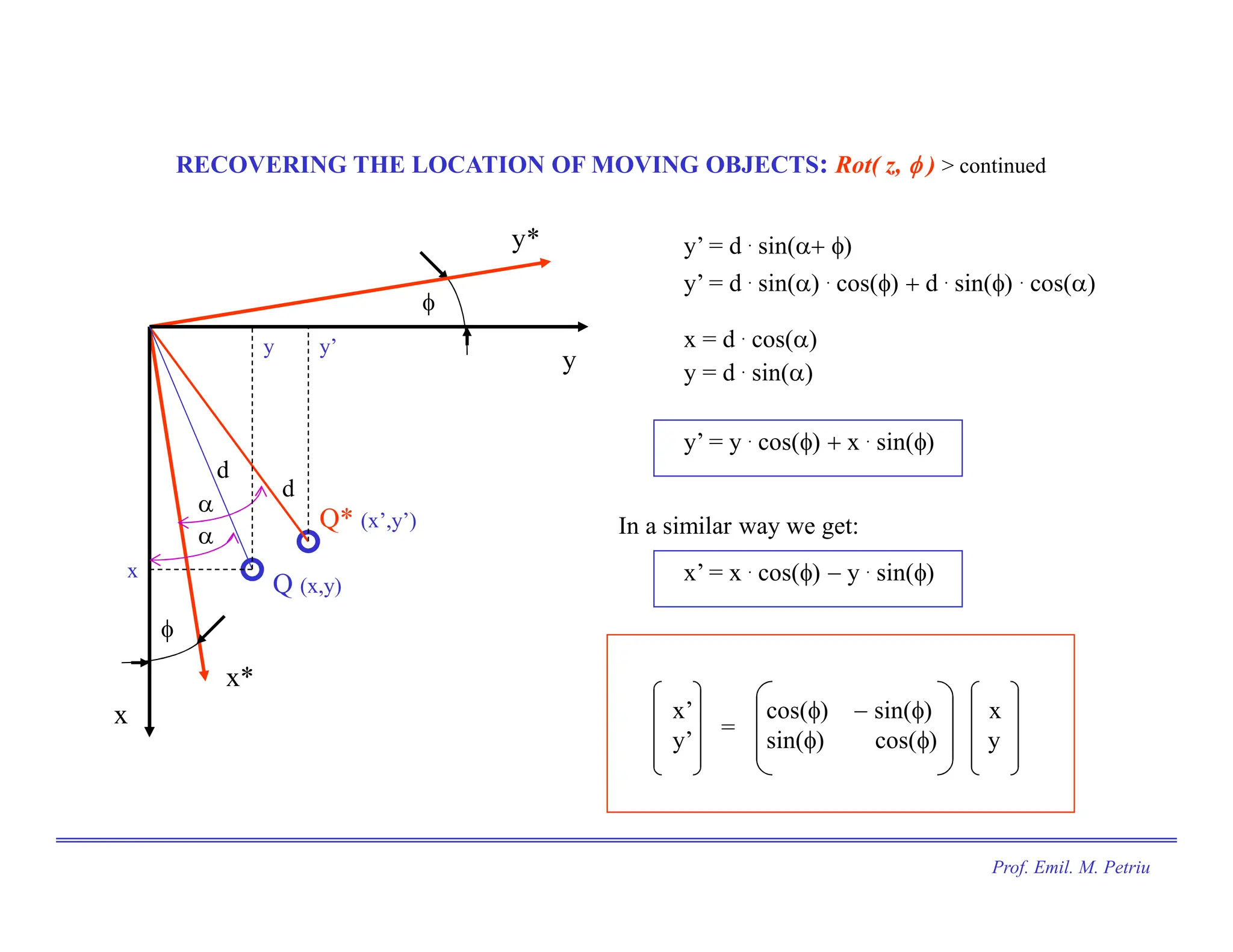
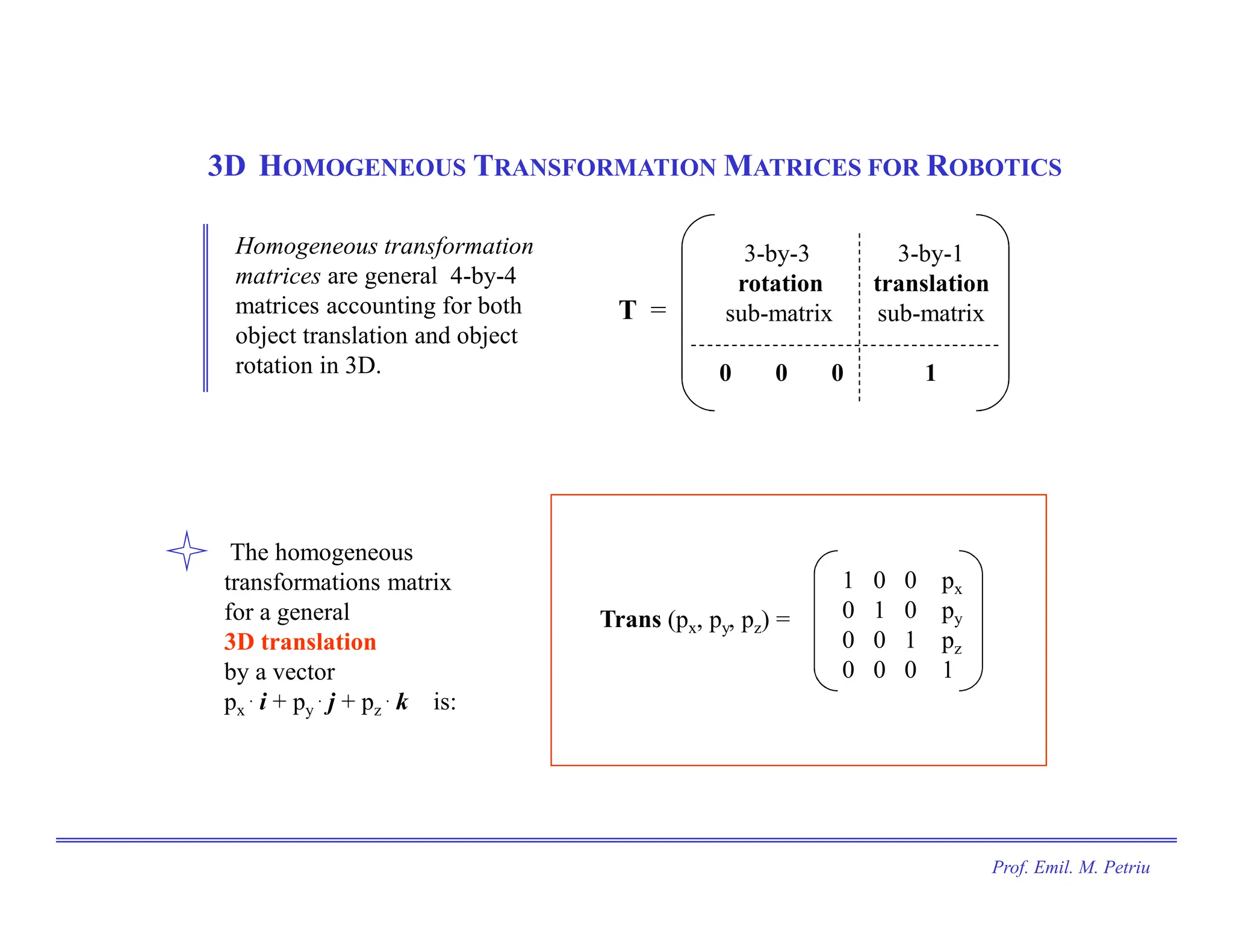
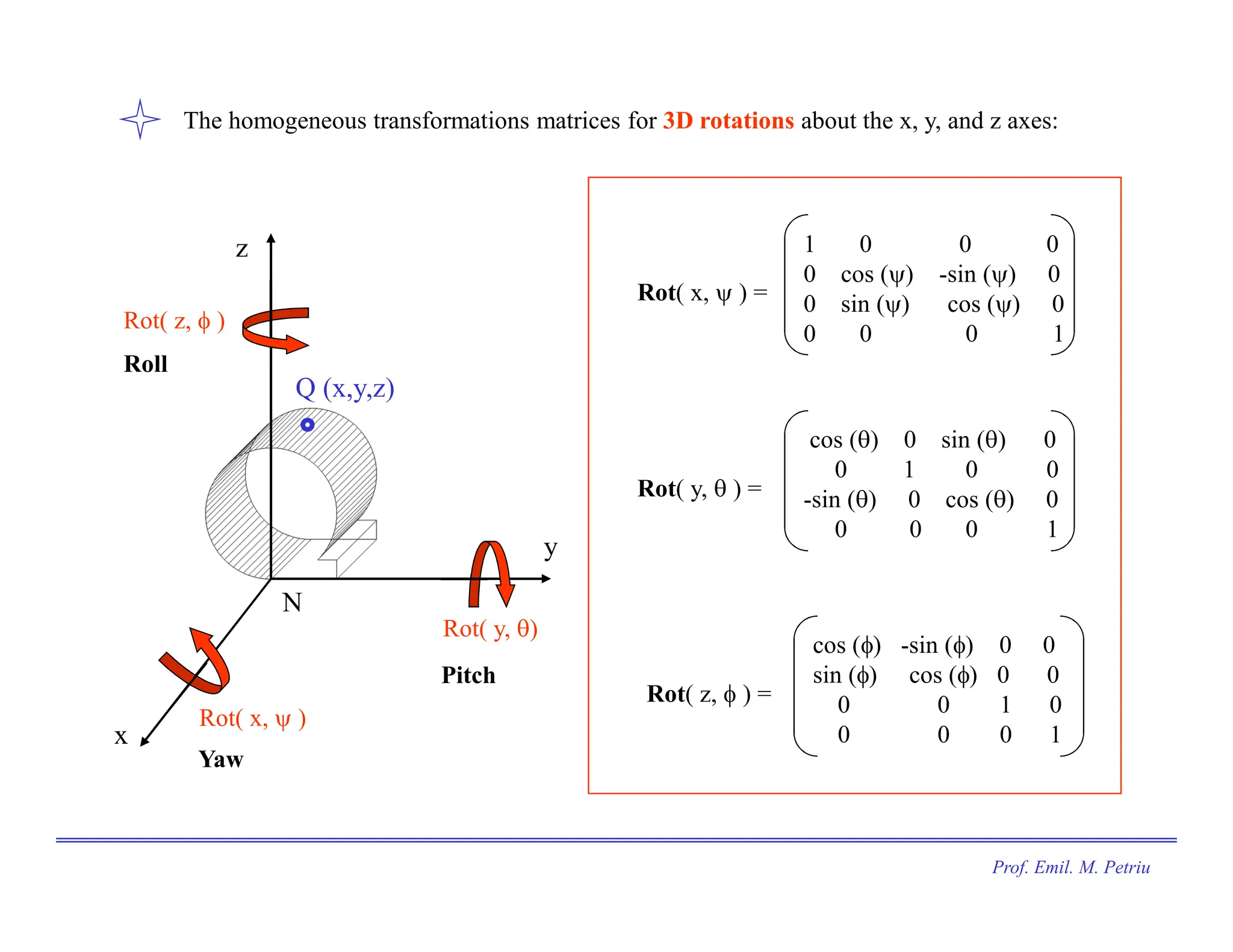
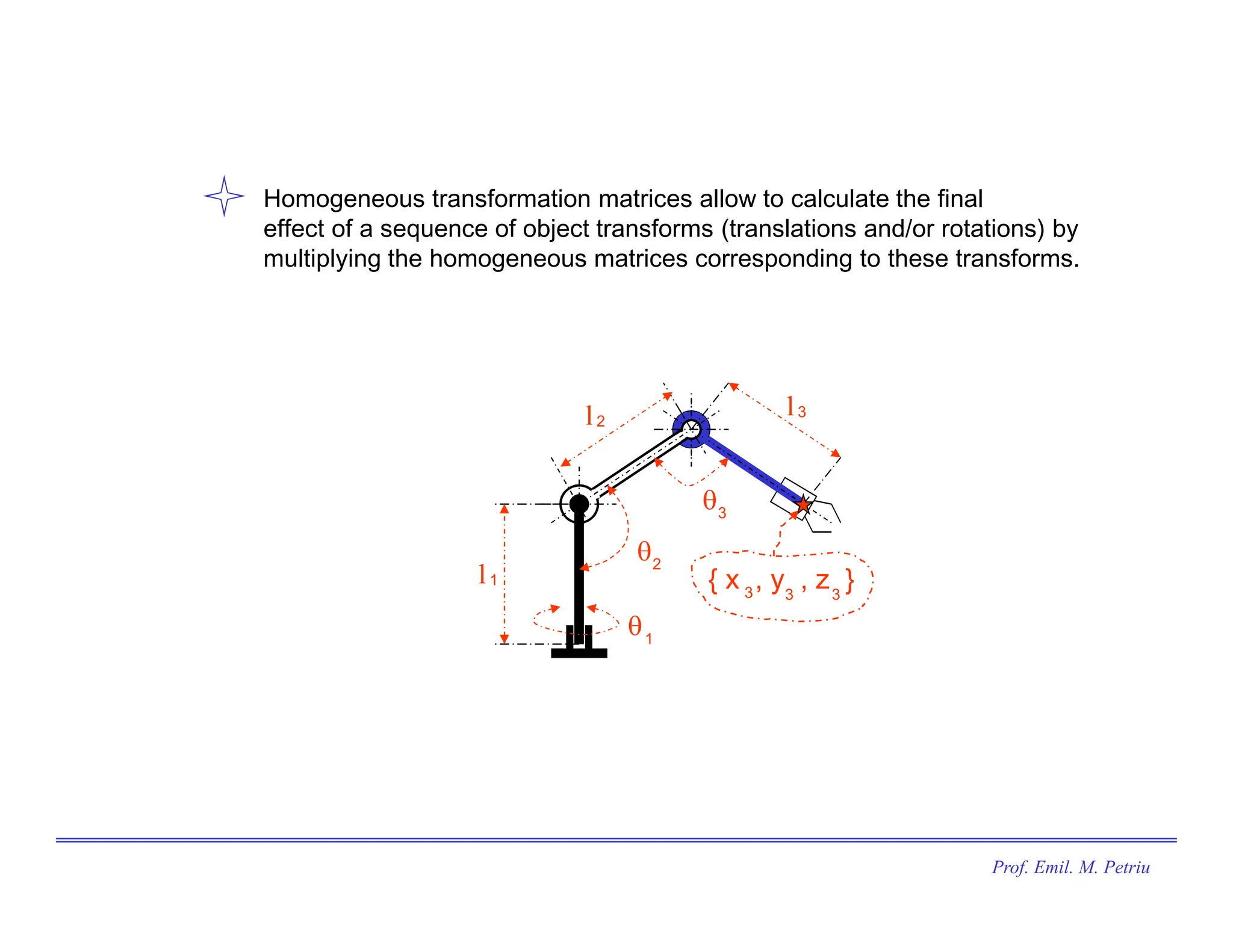
The document discusses the use of Cartesian coordinates in robotics and computer graphics, emphasizing the application of homogeneous transformation matrices for calculating the position of moving objects through translations and rotations. It outlines the decomposition of 3D rotations into roll, pitch, and yaw, and provides formulas for homogeneous transformation matrices that represent these transformations. The document illustrates how these matrices can be combined to determine the overall effect of multiple transformations on an object.

1. Prof. Emil. M. Petriu
CARTESIAN COORDINATES
x
y
z
Cartesian coordinates
used in robotics
z
x
y
Cartesian coordinates
used in computer
graphics
Corkscrew rule
(right-hand rule)
to define positive
directions of the
axes
HOMOGENEOUS TRANSFORMATION MATRICES

2. x0
y0
z0
R
q
R y1
x1
z1
N
q
N
y1
x1
z1
N*
q
N
Q*
r
R
p
R
P*
R
Q
q*
R
RECOVERING THE LOCATION OF MOVING OBJECTS: TRANSLATION
q* = p* + q
R R N
p* = p + r
R R R
q* = p + q + r
R R R
N
q = p + q
R R N
Using a reference frame N affixed to the object allows the calculation of the variable
location of the point Q on the moving object in a given reference frame R as the sum
of two vectors, a constant one representing the location of Q relative to N and another
variable representing the location of N relative to R:
Recovering the 3D location of a point on a moving object
in a given reference frame R. when the object suffers only
a translation movement relative to R..
Prof. Emil. M. Petriu

3. RECOVERING THE LOCATION OF MOVING OBJECTS: ROTATION
x0
y0
z0
R
p
R
q
N
y1
x1
z1
N
Q
ROT
q* = ?
R
Recovering the 3D location of a point on an object
rotating in a given reference frame R.
y1
x1
z1
N*
q
N
Q*
p
R
x0
z0
y0
Vectors can not
describe the rotation !
q* = ?
R
Prof. Emil. M. Petriu

4. RECOVERING THE LOCATION OF MOVING OBJECT: ROTATION > continued
x0
y0
z0
R
p
R
q
N
y1
x1
z1
N
Q
ROT
y1
x1
z1
N
Rot( x, ψ )
Rot( y, θ)
Rot( z, φ )
y1
x1
z1
N*
q
N
Q*
p
R
Prof. Emil. M. Petriu

5. x0
y0
z0
R
p
R
q
N
y1
x1
z1
N
Q
RECOVERING THE LOCATION OF MOVING OBJECT: ROTATION > continued
ROT
y1
x1
z1
N
Rot( x, ψ )
Rot( y, θ)
Rot( z, φ )
The general rotation of an object in 3D
can be conveniently decomposed into a
sequence of three elementary rotations
about the axes of the Cartesian reference
frame attached to that object, namely:
Rot( z, φ ) a rotation about z-axis, “roll,”
by an angle φ ;
Rot( y, θ) a rotation about y-axis, “pitch,”
by an angle θ ;
Rot( x, ψ ) a rotation about x-axis, “yaw,”
by an angle ψ .
Prof. Emil. M. Petriu

6. x0
y0
z0
R
p
R
q
N
y1
x1
z1
N
Q
RECOVERING THE LOCATION OF MOVING OBJECT: ROTATION > continued
ROT
y1
x1
z1
N
Rot( x, ψ )
Rot( y, θ)
Rot( z, φ )
y1
x1
z1
N*
q
N
Q*
p
R
RPY
The general rotation in 3D is often known as the
RPY rotation , a name reminding of the Roll,
Pitch, and Yaw components.
Prof. Emil. M. Petriu

7. RECOVERING THE LOCATION OF MOVING OBJECT: ROTATION >> continued
q
N
Q
y
x
z
N
Rot( x, ψ )
Rot( y, θ)
Rot( z, φ )
Roll
Pitch
Yaw
y
x
z
N
Q*
z*
x*
y*
Prof. Emil. M. Petriu

8. RECOVERING THE LOCATION OF MOVING OBJECTS: Roll, Rot( z, φ
φ
φ
φ )
y
x
z
Rot( z, φ )
Roll
N
x
y
z Q (x,y,z)
Q* (x’,y’,z’)
y
x
z
x*
y*
z’ = z
y’
x’
φ
φ
Prof. Emil. M. Petriu

9. RECOVERING THE LOCATION OF MOVING OBJECTS: Rot( z, φ
φ
φ
φ ) > continued
φ
y*
Q* (x’,y’)
φ
x*
x
y
Q (x,y)
α
α
d
d
y’ = d . sin(α+ φ)
y’
y’ = d . sin(α) . cos(φ) + d . sin(φ) . cos(α)
y
y = d . sin(α)
x
x = d . cos(α)
y’ = y . cos(φ) + x . sin(φ)
x’ cos(φ) − sin(φ) x
y’ sin(φ) cos(φ) y
=
x’ = x . cos(φ) − y . sin(φ)
In a similar way we get:
Prof. Emil. M. Petriu

10. 3D HOMOGENEOUS TRANSFORMATION MATRICES FOR ROBOTICS
3-by-3 3-by-1
rotation translation
sub-matrix sub-matrix
0 0 0 1
T =
Homogeneous transformation
matrices are general 4-by-4
matrices accounting for both
object translation and object
rotation in 3D.
The homogeneous
transformations matrix
for a general
3D translation
by a vector
px
. i + py
. j + pz
. k is:
Trans (px, py, pz) =
1 0 0 px
0 1 0 py
0 0 1 pz
0 0 0 1
Prof. Emil. M. Petriu

11. Q (x,y,z)
y
x
z
N
Rot( z, φ )
Roll
Rot( y, θ)
Pitch
Rot( x, ψ )
Yaw
Rot( x, ψ ) =
1 0 0 0
0 cos (ψ) -sin (ψ) 0
0 sin (ψ) cos (ψ) 0
0 0 0 1
Rot( y, θ ) =
cos (θ) 0 sin (θ) 0
0 1 0 0
-sin (θ) 0 cos (θ) 0
0 0 0 1
Rot( z, φ ) =
cos (φ) -sin (φ) 0 0
sin (φ) cos (φ) 0 0
0 0 1 0
0 0 0 1
The homogeneous transformations matrices for 3D rotations about the x, y, and z axes:
Prof. Emil. M. Petriu

12. Homogeneous transformation matrices allow to calculate the final
effect of a sequence of object transforms (translations and/or rotations) by
multiplying the homogeneous matrices corresponding to these transforms.
Prof. Emil. M. Petriu
θ1
θ2
θ3
l1
l2
l3
{ x , y , z }
3 3 3