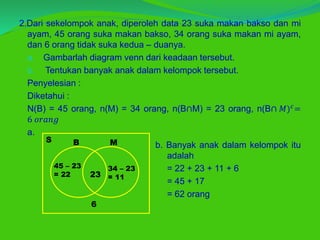
Dokumen tersebut membahas tentang pengertian himpunan, notasi dan anggota himpunan, menyatakan suatu himpunan, himpunan berhingga dan tak berhingga, himpunan kosong dan semesta, himpunan bagian, serta diagram Venn. Secara singkat, himpunan adalah kumpulan objek yang dapat didefinisikan anggotanya, anggota himpunan ditulis dengan kurung kurawal, dan terdapat berbagai cara untuk menyatakan

1. KELAS ; VII

2. HIMPUNAN
A. HIMPUNAN
1. Pengertian Himpunan
Perhatikan lingkungan di sekitar kalian. Pasti
dengan mudah kalian dapat menemukan kumpulan
atau kelompok berikut ini :
a. Kumpulan hewan berkaki dua
b. Kumpulan warna lampu lalu lintas
c. Kelompok tanaman hias
Dari kumpulan yang tersebut diatas pasti kalian
bisa menyebutkannya
1. Kumpulan hewan berkaki dua diantaranya :
ayam, itik, angasa, dan seterusnya.

3. 2. Kumpulan warna lampu lalu lintas diantaraya:
merah, kuning, dan hijau
3. Kelompok tanaman hias diantaranya : bunga
anggrek, bunga mawar, bunga melati dan
seterusnya,
Dari sekumpulan yang disebutkan tersebut ternyata
sangat jelas disebutkan anggotanya atau obyeknya,
maka dapat kita menarik kesimpulan mengenai definisi
dari himpunan tersebut.
Himpunan adalah kumpulan benda atau objek yang dapat
didefinisikan dengan jelas, sehingga dengan tepat dapat
diketahui objek yang termasuk himpunan dan yang tidak
termasuk dalam himpunan tersebut.
Sekarang perhatikan kumpulan berikut ini :
1. Kumpulan lukisan indah
2. Kumpulan wanita cantik di Indonesia
Apakah dari kumpulan tersebut di atas dapat di
sembutkan objeknya ?

4. Dari contoh tersebut maka :
1. Kumpulan lukisan indah tidak dapat disebutkan
dengan jelas objeknya sehingga tidak termasuk ke
dalam suatu himpunann.
2. Kumpulan wanita cantik di Indonesia juga tidak
termasuk ke dalam suatu himpunan karena
objeknya tidak jelas.
Dari contoh di atas dapat kita menarik suatu
kesimpulan bahwa :
Suatu kumpulan dapat di katakan sebagai suatu
himpunan jika objeknya dapat disebutkan dengan
jelas sedangkan suatu kumpulan tidak dapat
dikatakan sebagai himpunan jika objeknya tidak bisa
disebutkan dengan jelas.

5. 2. Notasi dan Anggota Himpunan
Suatu himpunan biasanya diberi nama atau dilambangkan dengan
huruf besar (kapital) A, B, C, …, Z. Adapun benda atau objek yang
termasuk dalam himpunan tersebut ditulis dengan menggunakan
pasangan kurung kurawal { … }.
Contoh :
Nyatakan himpunan berikut dengan menggunakan tanda kurung
kurawal.
1. A adalah himpunan bilangan cacah kurang dari 6
2. P adalah himpunan huruf – huruf vokal
3. Q adalah himpunan tiga binatang buas.
Penyelesaian :
1. A adalah himpunan bilangan cacah kurang dari 6
Anggota himpunan bilangan cacah kurang dari 6 adalah : 0, 1, 2, 3,
4, 5
Jadi, A = { 0, 1, 2, 3, 4, 5 }

6. 2. P adalah himpunan huruf – huruf vokal
Anggota himpunan P adalah : a, i, u, e, o
Jadi, P = { a, i, e, o }
3. Q adalah himpunan tiga binatang buas
Anggota himpunan Q adalah : harimau, singa, srigala
Jadi, Q = { harimau, singa, srigala }
Setiap benda atau objek yang berada dalam suatu himpunan
disebut anggota atau elemean dari himpunan itu dan di
notasikan dengan ∈.
Adapun benda atau objek yang tidak termasuk ke dalam suatu
himpuan dikatakan bukan anggota himpunan dan di notasikan
dengan ∉.
Banyaknya anggota suatu himpunan A dinyatakan dengan
𝑛(𝐴)

7. Contoh :
1. Diketahui A = {1, 2, 3, 4, 5}maka :
1 ∈ A 2 ∈ A 3 ∈ A 4 ∈ A 5 ∈ A dan 6 ∉ A
2. Diketahui C = {0, 1, 2, 3, 4, 5}
Tentukan banyak anggota himpunan C!
Jawab :
0, 1, 2, 3, 4, 5, adalah anggota dari himpunan C maka :
𝑛 𝐶 = 6.
Ada beberapa lambang himpunan bilangan sebagai berikut :
A : lambang himpunan bilangan asli, A = {1,2,3, …}
B : lambang himpunan bilangan bulat, B = {…, -3, -2, -1, 0, 1, 2, 3, … }
C : Lambang himpunan bilangan cacah, C = {0, 1, 2, 3, … }
L : Lambang bilangan ganjil
N : lambang bilangan genap
P : lambang bilangan prima ,dst

8. 3. Menyatakan Suatu Himpunan
Suatu himpunan dapat dinyatakan dengan tiga cara
sebagai berikut :
a. Dengan Kata – kata
Dengan cara menyebutkan semua syarat/sifat
keanggotaannya.
Contoh :
P adalah himpunan bilangan prima antara 10 dan 40
Ditulis : P = {bilangan Prima antara 10 dan 40}
b. Dengan notasi pembentuk himpunan
Dengan cara menyebutkan semua syarat/sifat
keanggotaannya,namun anggota himpunannya
dinyatakan dengan peubah (x atau y).
Contoh :
P = {bilangan prima antara 10 dan 40}
Notasi pembentuk himpunannya :
P={x/10<x<40, x ∈ bilangan prima}

9. c. Dengan mendaftar anggota – anggotanya.
Dengan menyebutkan anggota – anggotanya di dalam
kurung kurawal.
Contoh :
P = {bilangan prima antara 10 dan 40}
P = {11, 13, 17, 19, 23, 29, 31, 37}
4. Himpunan berhingga dan Himpunan Tak Berhingga
a. Himpunan Berhingga adalah himpunan yang
memiliki banyak anggota berhingga.
Contoh :
A = { Bilangan asli < 10}
C = {1, 2, 3, …, 20}
b. Himpunan tak berhingga adalah himpunan yang
memiliki anggota tak berhingga
Contoh :
A = {1, 2, 3, … }
P = { Bilangan prima}

10. B. Himpunan Kosong dan Himpunan Semesta
1. Himpunan Kosong
Himpunan Kosong adalah suatu himpunan yang tidak
mempunyai anggota.
Himpunan kosong disimbulkan dengan”{ } atau ∅”
Contoh :
M={bilangan ganjil yang dihabis di bagi 2},maka :
M = { } karena M tidak ada anggotanya.
{ } ≠ { 0 }
Karena { 0 } bukan himpunan kosong tapi termasuk
kedalam suatu himpunan karena memiliki satu anggota
yaitu 0 (nol)

11. 2. Himpunan Semesta
Gambar di samping menunjukkan
kelompok buah – buahan yang terdiri
atas apel, anggur, jeruk dan jambu.
Jika P = {apel, anggur, jeruk, jambu}
maka semesta pembicaraan dari
himpunan P adalah S = {buah –
buahan}.
Dengan kata lain, S adalah himpunan semesta dari P. Himpunan S
memuat semua anggota himpunan P.
Dari keterangan di atas maka kita dapat menarik kesimpulan dari
definisi himpunan semesta.
Himpunan semesta adalah himpunan yang memuat semua
anggota atau objek himpuan yang dibicarakan. Himpunan
semesta (semesta pembicaraan) biasanya dilambangkan dengan
“ S “.

12. Contoh :
Tentukan tiga himpunan semesta yang mungkin dari himpunan
berikut ini :
1. {2, 3, 5,7}
Jawab :
Misalkan A = {2, 3, 5,7}, maka himpunan semesta yang mungkin
dari himpunan A adalah:
S = {bilangan prima}
S = {bilangan asli}
S = {bilangan cacah}
2. {kerbau, sapi, kambing}
Jawab :
S = {binatang}
S = { binatang berkaki empat}
S = { binatang menyusui}

13. SOAL – SOAL LATIHAN
1. Diantara himpunan berikut, manakah yang termasuk himpunan
kosong.
a. Himpunan kelas VII SMP yang berumur kurang dari 8 tahun.
b. Himpunan bilangan prima yang habis di bagi 2
c. Himpunan bilangan asli antara 8 dan 9
2. Tentukan sebuah himpunan semesta yang mungkin untuk himpunan
berikut :
a. E = {m, dm, cm, mm}
b. F = {kerucut, tabung, bola}
c. A = {1, 3, 5, 7, . . .}
3. Sebutkan paling sedikit dua buah himpunan semesta yang mungkin
dari tiap himpunan berikut :
a. P = {yamaha, honda, suzuki}
b. G = {x/x = 2n, n ∈ bilangan cacah}

14. C. HIMPUNAN BAGIAN
1. Pengertian Himpunan Bagian
Perhatikan himpunan – himpunan berikut ini :
A = {1, 2, 3}
B = {4, 5, 6}
C = {1, 2, 3, 4, 5, 6}
Berdasarkan ketiga himpunan di atas, tampak
bahwa setiap anggota himpunan A, yaitu 1, 2, 3
juga menjadi anggota himpunan C. Dalam hal ini
dikatakan bahwa himpunan A merupakan himpunan
bagian dari C, ditulis A ⊂ C atau C ⊃ A.
Kesimpulan :
Himpunan A merupakan himpunan bagian B, jika setiap
anggota A juga menjadi anggota B dan dinotasikan
dengan “ A ⊂ B atau B ⊃ A.

15. Perhatikan himpunan B dan himpunana C
B = {4, 5, 6}
C = {1, 2, 3, 4, 5}
Dari kedua himpunan tersebut tampak bahwa tidak semua
anggota B menjadi anggota himpunan C, karena 6 ∉ C.
Dikatakan bahwa B bukan merupakan bagian dari C, ditulis
B ⊄ C.
Kesimpulan :
Himpunan A bukan merupakan himpunan bagian dari B,
jika terdapat anggota A yang bukan anggota himpunan
B,dan dinotasikan dengan “ A ⊄ B

16. 2. Menentukan banyaknya Himpunan Bagian dari Suatu Himpunan
a. Himpunan Kosong merupakan bagian dari setiap himpunan
b. Setiap himpunan merupakan himpunan bagian dari himpunan itu
sendiri.
Untuk mengetahui banyaknya himpunan bagian dari suatu himpunan
perhatikan tabel berikut ini :
Himpunan Banyaknya
anggota
Himpunan bagian Banyaknya Himpunan
bagian
{a} 1 { } {a} 2 = 21
{ a, b } 2 { } {a} {b} {a, b} 4 = 22
{a, b, c} 3 { }, {a}, {b}, {c},{a,b},{a,c},{b,c},
{a,b,c}
8 = 23
{a,b,c,d} 4 { },{a},{b},{c},{d},{a,b}
{a,c},{a,d},{b,c},{b,d}
{c,d},{a,b,c,},{a,b,d},
{a,c,d},{b,c,d},
{a,b,c,d}
2 = 24
{a,b,c, . .. } n { },{a},{b},{c},… 2 𝑛

17. Berdasarkan tabel tersebut, tampak bahwa terdapat hubungan antara
banyaknya anggota suatu himpunan dengan banyaknya himpunan
bagian himpunan tersebut.
Dengan demikian, dapat disimpulkan sebagai berikut :
Banyaknya semua himpunan bagian dari suatu himpunan adalah 2 𝑛
,
dengan n banyaknya anggota himpunan tersebut.
Contoh :
Tentukan banyaknya himpunan bagian dari {a, b, c, d, e}?
Jawab :
{a, b, c, d, e}
n = 5 maka :
2 𝑛 = 25
= 2 x 2 x 2 x 2 x 2
= 32
Jadi banyak himpunan bagian {a, b, c, d, e} adalah : 32

18. D. DIAGRAM VENN
Cara yang mudah untuk kita menyatakan suatu himpunan adalah
dengan gambar atau diagram venn.
Dalam membuat suaut diagram venn, perlu diperhatikan beberapa hal
antara lain :
1. Himpunan semesta biasanya digambarkan dengan bentuk persegi
panjang
2. Setiap himpunan lain yang sedang dibicarakan digambarkan
dengan lingkaran atau kurva tertutup sederhana
3. Setiap anggota himpunan ditunjukkan dengan noktah atau titik
4. Jika banyak anggota himpunannya tak berhingga, maka masing –
masing anggota himpunan tidak perlu digambarkan dengan titik,

19. Contoh :
1. Diketahui S = { a, b, c, d, e, f, g, h}
P = { a, b, c, d}
Q = { e, f, g }
Gambarlah diagram venn himpunan tersebut
2. Diketahui : S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 3, 4, 5}
B = { 4, 5, 6, 7, 8}
Gambarlah diagram venn himpunan tersebut !
S P Q
.a
.b
.c
.d
.e
.f
.g
.h

20. Jawab :
3. Jika S = {Siswa SMPN 4 Masbagik}
M = {Siswa Kelas VII}
N = {Siswa Kelas IX}
Gambarlah diagram venn data tersebut !
Jawab :
S A B
.4
.5
.1
.2
.3
.6
.7
.8
.9 .10
S M N

21. SOAL LATIHAN
1. Gambarlah diagrram venn dari masing – masing soal di bawah ini
:
a. S = {x/x < 20, x bilangan cacah},
O = {1, 4, 9, 16}, dan
P = {1, 2, 3, 4, 5}
b. S = {0, 1, 2, 3, . . ., 15}
M = {3, 5, 7, }, dan
P = {2, 3, 4, . . . , 12}
2. Perhatikan diagram venn di bawah ini !
a. Himpunan yang ada pada K dan T
b. Himpunan S yang ada di K tetapi tidak
ada di T
c. Himpunan T tetapi tidak ada di K
d. Himpunan yang tidak termasuk di K
maupun di T
S
K T
.d
.e
.c
.0
.4
.6
.8
.f
.g
.h
.a
.b
.1 .2
.3

22. E. HUBUNGAN ANTAR HIMPUNAN
1. Himpunan Saling Lepas
Dua himpunan dikatakan saling lepas atau saling asing bila
kedua himpunan itu tidak memp[unyai anggota
persekutuan.
Contoh :
P = {1, 2, 3, 4, 5}
Q = {6, 7, 8, 9, 10}
S
.1
.2
.3
.4
.5
.6
.7
.8
.9
.10
P P

23. 2. Himpunan Tidak Saling Lepas
Dua himpunan dikatakan tidak saling lepas bila kedua himpunan itu
mempunyai anggota persekutuan.
Contoh :
A = {a, b, c, d, e}
B = {d, e, f, g, h}
3. Himpunan yang Sama (=)
Dua himpunan dikatakan sama bila keduanya mempunyai anggota
yang sama. A = B
Contoh :
M = {1, 2, 3, 4, 5}
N = {1, 2, 3, 4, 5}
S
.a
.b
.c
.d
.e
.f
.g
.h
A B
S A=B
.1
.2
.3
.5
.4

24. 4. Himpunan yang Ekuivalen (~)
Dua himpunan dikatakan ekuivalen jika kedua anggota himpunan
mempunyai jumlah anggota yang sama.
Contoh :
P = {1, 2, 3, 4}
Q = {a, b, c, d}
S
.1
.2.3
.4
.a
.b
.c
.d
P Q

25. E. OPERASI HIMPUNAN
1.IRISAN DUA HIMPUNAN (∩)
a. Pengertian Irisan Dua Himpunan
Misalkan : A = {1, 2, 3, 4, 5}
B = { 3, 4, 5, 6,7}
Anggota himpunan A dan B adalah anggota himpunan A dan
sekaligus menjadi anggota himpunan B = {3, 4, 5}
Selanjutnya, anggota persekutuan dua himpunan disebut
irisan dua himpunan dan dinotasikan dengan “∩ “
Jadi, A ∩ B = {3, 4, 5}
Secara umum dapat dikatakan sebagai berikut :
𝐼𝑟𝑖𝑠𝑎𝑛 (𝑖𝑛𝑡𝑒𝑟𝑠𝑒𝑘𝑠𝑖) dua himpunan adalah suatu himpunan
yang anggotanya merupakan anggota persekutuan dari dua
himpunan tersebut.
Irisan dua himpunan A dan B dinotasikan dengan :
𝐴 ∩ 𝐵 = { 𝑥
𝑥 ∈ 𝐴 𝑑𝑎𝑛 𝑥 ∈ 𝐵}

26. b. Menentukan Irisan Dua Himpunan
Contoh :
Diketahui : A = {2, 3, 5} dan
B = {1, 2, 3, . . . , 10}
a. Tentukan 𝐴 ∩ 𝐵 !
b. Gambarlah diagram venn 𝐴 ∩ 𝐵 !
Penyelesaian :
a. A ∩ B = {2, 3, 5} ∩ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A ∩ B = {2, 3, 5}
b. Gambar diagram venn A ∩ B
S
B
A
.2
.3
.5
.1
.4
.6
.7 .8
.9
.10

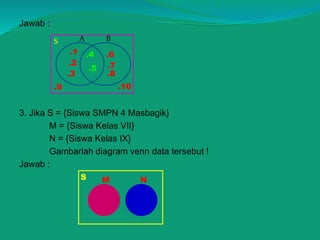
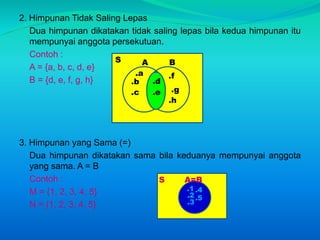
27. 2. Diketahui :
M = {a, b, c, d,e, f}
N = {d, e, f, g, h, i]
a. Tentukan M ∩ N
b. Gambarlah diagram venn M ∩ N
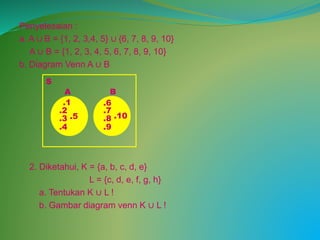
Penyelesaian :
a. M ∩ N = {a, b, c, d, e, f} ∩ {d, e, f, g, h, i}
M ∩ N = {d, e, f}
b. Diagram Venn M ∩ N
M
S
.i
.e
.f
N
.h
.g
.c
.b
.a
.d

28. 3. Diketahui :
K = {1, 4, 9,16, 25}
L = {1, 4, 9, 16, 25}
a. Tentukan K ∩ L
b. Gambarlah diagram venn K ∩ L
Penyelesaian :
a. K ∩ L = {1, 4, 9, 16, 25} ∩ {1, 4, 9, 16, 25}
K ∩ L = { 1, 4, 9, 16, 25}
Artinya bahwa K = L
b. Diagram venn K ∩ L
K = L
S
.1
.4 .9
.16
.25

29. 2. GABUNGAN DUA HIMPUNAN
a. Pengertian gabungan (Union) dua himpunan
Jika A dan B adalah dua buah himpunan , gabungan himpunan A
dan B adalah himpunan yang anggotanya terdiri atas anggota –
anggota A atau anggota – anggota B.
Dengan notasi pembentuk himpunan, gabungan A dan B
dituliskan sebagai berikut :
𝐴 ∪ 𝐵 = { 𝑥
𝑥 𝜖 𝐴 𝑎𝑡𝑎𝑢 𝑥 𝜖 𝐵 }
Catatan : “∪ “ dibaca gabungan atau union
b. Menentukan Gabungan Dua Himpunan
Contoh :
Diketahui : A = {1, 2, 3, 4, 5}
B = {6, 7, 8, 9, 10}
Tentukan :
a. 𝐴 ∪ 𝐵
b. Gambarlah diagram venn 𝐴 ∪ 𝐵 !

30. Penyelesaian :
a. A ∪ B = {1, 2, 3,4, 5} ∪ {6, 7, 8, 9, 10}
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
b. Diagram Venn A ∪ B
2. Diketahui, K = {a, b, c, d, e}
L = {c, d, e, f, g, h}
a. Tentukan K ∪ L !
b. Gambar diagram venn K ∪ L !
S
A B
.1
.5
.4
.2
.3 .10
.9
.8
.7
.6

31. Penyelesaian :
a. K ∪ L = {a, b, c, d, e} ∪ {c, d, e, f, g, h}
K ∪ L = {a, b, c, d, e, f, g, h}
b. Diagram venn K ∪ L
S
K L
.a
.b
.c
.d
.e
.f
.g
.h

32. 4. KOMPLEMEN SUATU HIMPUNAN
Komplemen himpunan A adalah suatu himpunan yang anggota –
anggotanya merupakan anggota S tetapi bukan anggota himpunan A.
Dengan notasi pembentuk himpunan dapat dituliskan sebagai berikut
: 𝐴 𝑐 𝐴′ = { 𝑥 𝑥 ∈ 𝑆 𝑑𝑎𝑛 𝑥 ∉ 𝐴 }
Komplemen A dinotasikan dengan “ 𝐴 𝑐
𝑎𝑡𝑎𝑢 𝐴′
Contoh :
Diketahui :
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 3, 4}
B = {2, 3, 5, 7}
Tentukan :
a. 𝐴 𝑐
b. 𝐵 𝑐
c. (𝐴 ∩ 𝐵) 𝑐

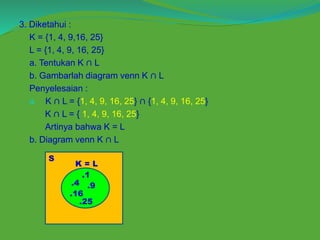
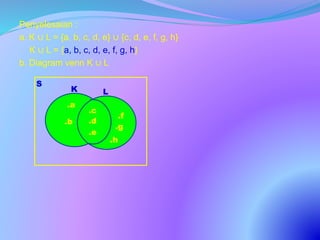
33. Penyelesaian :
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 3, 4}
B = {2, 3, 5, 7}
𝑎. 𝐴 𝑐 = {5, 6, 7, 8, 9, 10]
𝑏. 𝐵 𝑐 = {1, 4, 6, 8, 9, 10}
c. A ∩ B = {2, 3}
(𝐴 ∩ 𝐵) 𝑐
= {1, 4, 5, 6, 7, 8, 9, 10}
Diagram venn (𝐴 ∩ 𝐵) 𝑐
S
A B
.4
.1
.5
.7
.6
.8 .9 .10
.2
.3

34. 5. SELISIH (DIFFERENCE) DUA HIMPUNAN
Selisih (difference) himpunan A dan B adalah himpunan yang
anggotanya semua anggota dari A tetapi bukan anggota dari B.
Selisih himpunan A dan B dinotasikan dengan A – B atau A/B
Dengan notasi pembentuk himpunan dituliskan sebagai berikut :
A – B = { 𝑥 𝑥 ∈ 𝐴, 𝑥 ∉ 𝐵 }
𝐵 − 𝐴 = { 𝑥 𝑥 ∈ 𝐵, 𝑥 ∉ 𝐴 }
Contoh :
Diketahui : A = {a, b, c, d} dan B = {a, c, f, g}
A – B = {a, b, c, d} – {a, c, f, g}
= {b, d}
B – A = {a, c, f, g} – {a, b, c, d}
= {f, g}

35. 5. SIFAT – SIFAT OPERASI HIMPUNAN
a.Untuk setiap himpunan A dan B berlaku sifat komutatif irisan.
𝐴 ∩ 𝐵 = 𝐵 ∩ 𝐴
b. Untuk setiap himpunan A, B dan C berlaku sifat asosiatif irisan
𝐴 ∩ 𝐵 ∩ 𝐶 = 𝐴 ∩ ( 𝐵 ∩ 𝐶 )
c. Sifat idempotent irisan
𝐴 ∩ 𝐴 = 𝐴
d.Sifat identitas irisan
𝐴 ∩ 𝑆 = 𝐴
e. Sifat komplemen irisan
𝐴 ∩ 𝐴 𝑐
= 𝑎𝑡𝑎𝑢 ∅ (ℎ𝑖𝑚𝑝𝑢𝑛𝑎𝑛 𝑘𝑜𝑠𝑜𝑛𝑔)

36. f. Untuk setiap himpunan A, B,dan C berlaku sifat distributif irisan
terhadap gabungan.
𝐴 ∩ 𝐵 ∪ 𝐶 = 𝐴 ∩ 𝐵 ∪ ( 𝐴 ∩ 𝐶 )
g. Untuk setiap himpunan A, B, dan C berlaku sifat distributif gabungan
terhadap irisan
𝐴 ∪ 𝐵 ∩ 𝐶 = 𝐴 ∪ 𝐵 ∩ ( 𝐴 ∪ 𝐶 )
h. Untuk setiap himpunan A, B, dan C berlaku sifat distributif selisih
terhadap irisan
𝐴 − 𝐵 ∩ 𝐶 = 𝐴 − 𝐵 ∩ ( 𝐴 − 𝐶 )
i.Untuk setiap himpunan A, B, dan C berlaku sifat distributif selisih
terhadap gabungan.
𝐴 − 𝐵 ∪ 𝐶 = 𝐴 − 𝐵 ∪ ( 𝐴 − 𝐶 )
Menentukan banyak anggota dari gabungan dua himpunan dengan
menggunakan rumus sebagai berikut :
𝑛 𝐴 ∪ 𝐵 = 𝑛 𝐴 + 𝑛 𝐵 − 𝑛( 𝐴 ∩ 𝐵 )

37. 6.MENYELESAIKAN MASALAH DENGAN
MENGGUNAKAN KONSEP HIMPUNAN
Contoh :
1. Dalam suatu kelas yang terdiri atas 40 siswa, diketahui 24 siswa
yang suka bermain tenis, 23 siswa yang suka bermain sepak bola,
dan 11 siswa yang suka kedua – duanya.
a. Gambarlah diagram venn dari keterangan tersebut
b. Tentukan banyak siswa yang hanya suka bermain tenis
c. Tentukan banyak siswa yang hanya suka bermain sepak bola
d. Tentukan banyak siswa yang tidak suka kedua – duanya.
Penyelesaian :
Diketahui :
n(S) = 40 siswa
n(T) = 24 siswa
n(B) = 23 siswa
n(T ∩ B) = 11 siswa

38. a. Diagram venn data tersebut sebagai berikut :
b. Banyak siswa yang hanya
suku tenis
= 24 – 11
= 13 siswa
Jadi banyak siswa yang
hanya suka tenis
adalah 13 siswa.
c. Banyak siswa yang hanya suka sepak bola.
= 23 – 11
= 12 siswa
d. Banyak siswa yang tidak suka kedua – duanya
= n(s) – {n(T)saja + n(B)saja + n(T ∩ B)}
= 40 – (13 + 12 + 11)
= 40 – 36 = 4 siswa
S T B
11
24 – 11
= 13
23 – 11
= 12
4

39. 2.Dari sekelompok anak, diperoleh data 23 suka makan bakso dan mi
ayam, 45 orang suka makan bakso, 34 orang suka makan mi ayam,
dan 6 orang tidak suka kedua – duanya.
a. Gambarlah diagram venn dari keadaan tersebut.
b. Tentukan banyak anak dalam kelompok tersebut.
Penyelesian :
Diketahui :
N(B) = 45 orang, n(M) = 34 orang, n(B∩M) = 23 orang, n(B∩ 𝑀) 𝑐=
6 𝑜𝑟𝑎𝑛𝑔
a.
b. Banyak anak dalam kelompok itu
adalah
= 22 + 23 + 11 + 6
= 45 + 17
= 62 orang
S B M
6
23
45 – 23
= 22
34 – 23
= 11