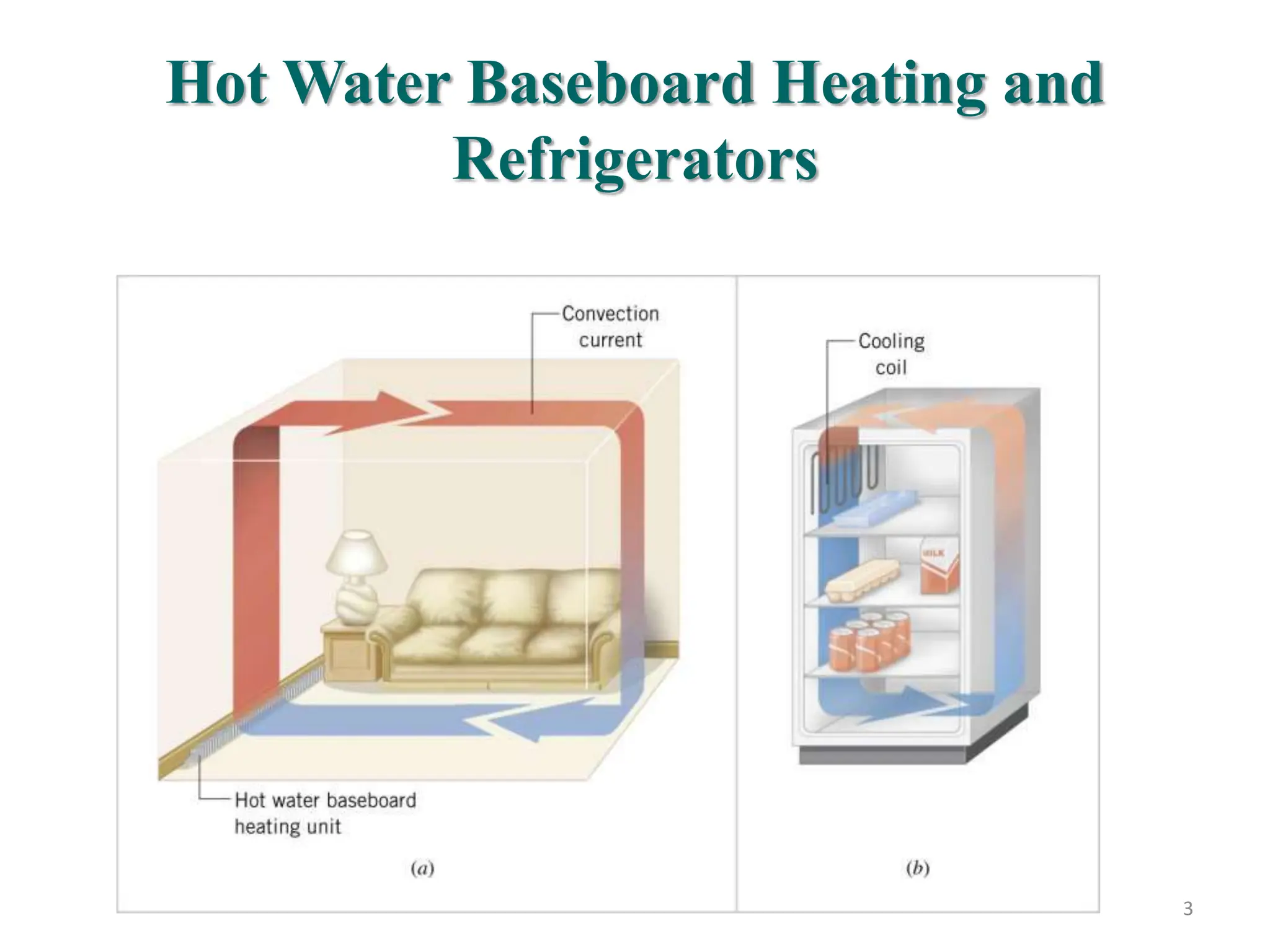
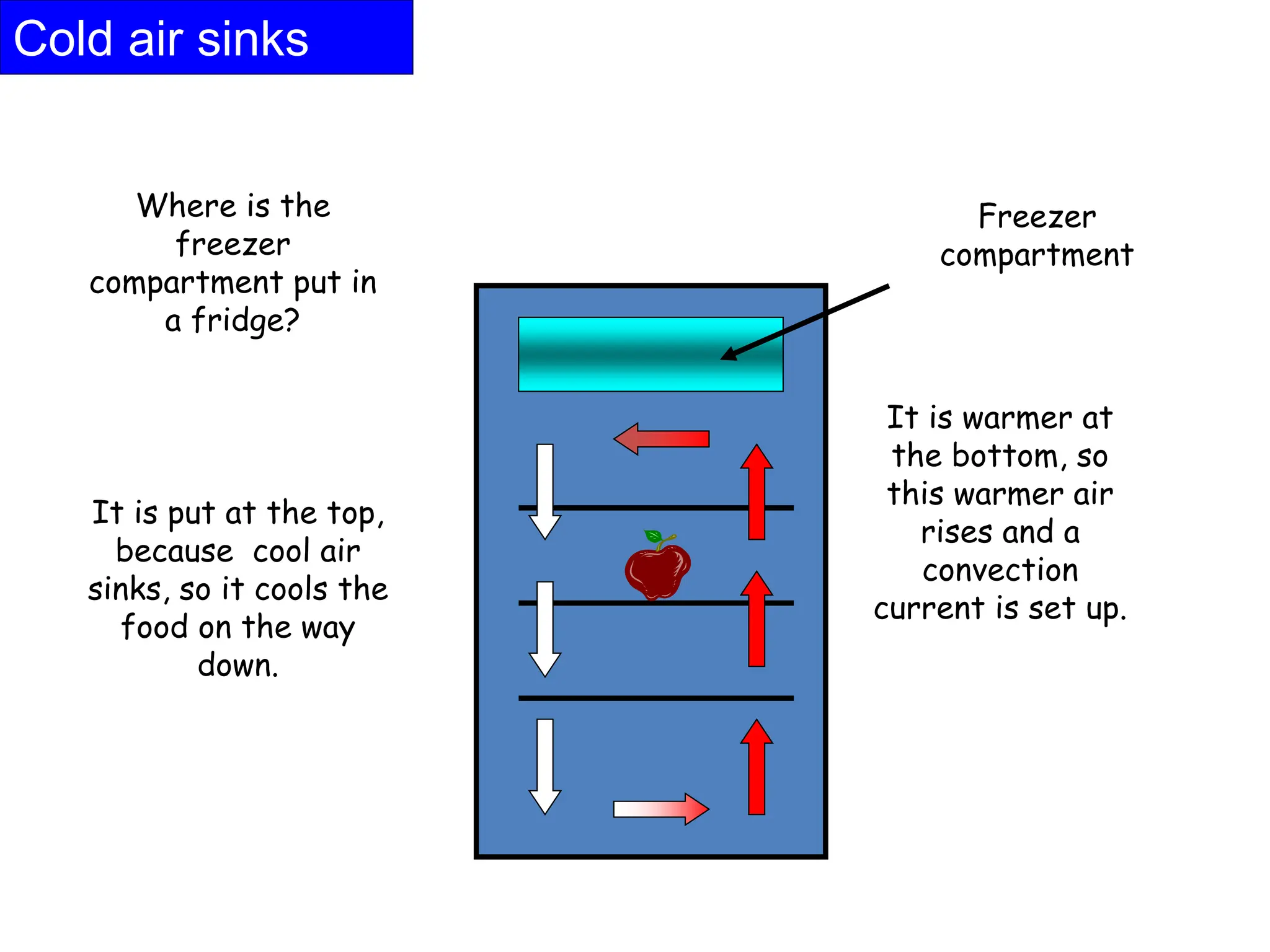
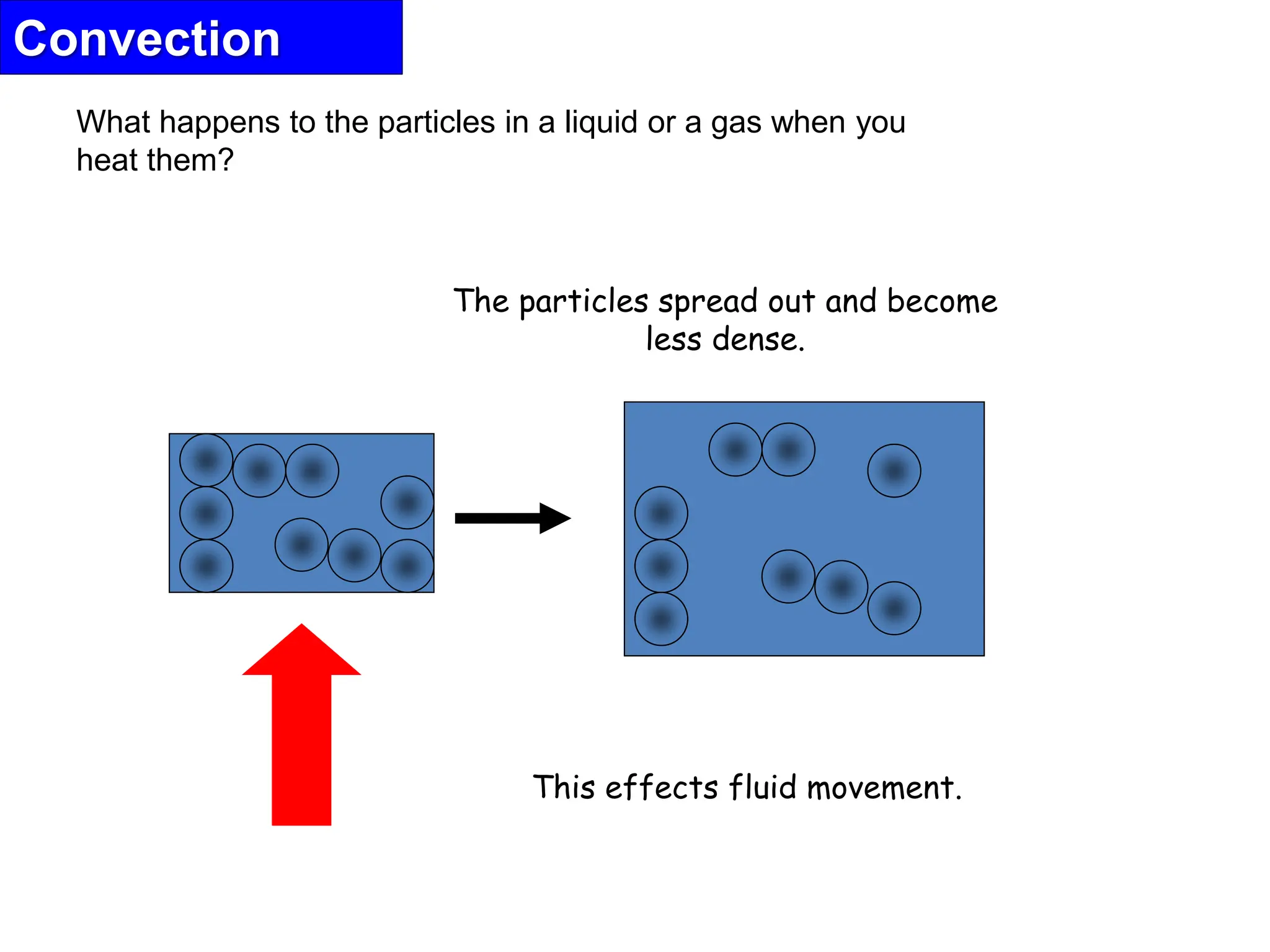
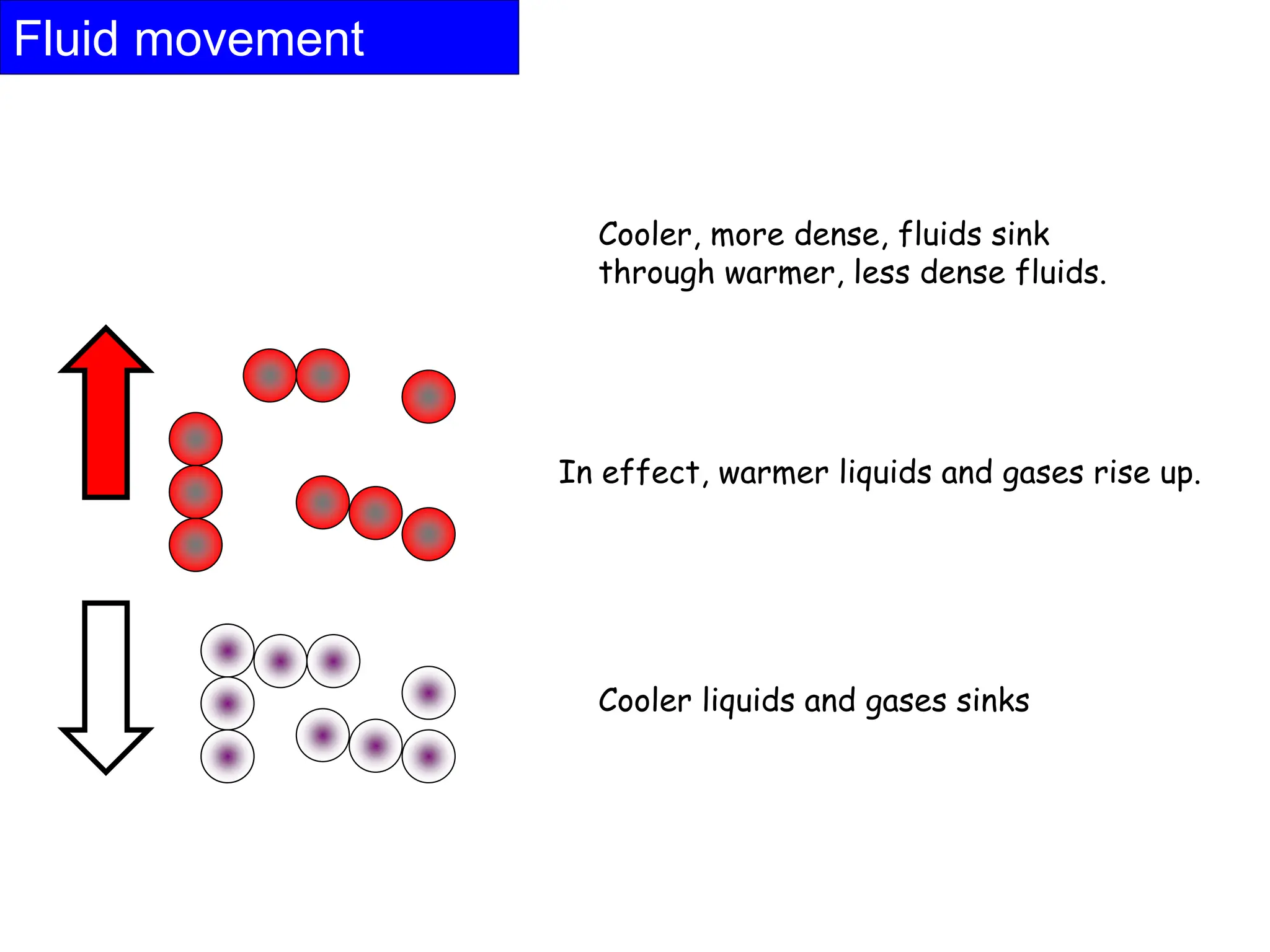
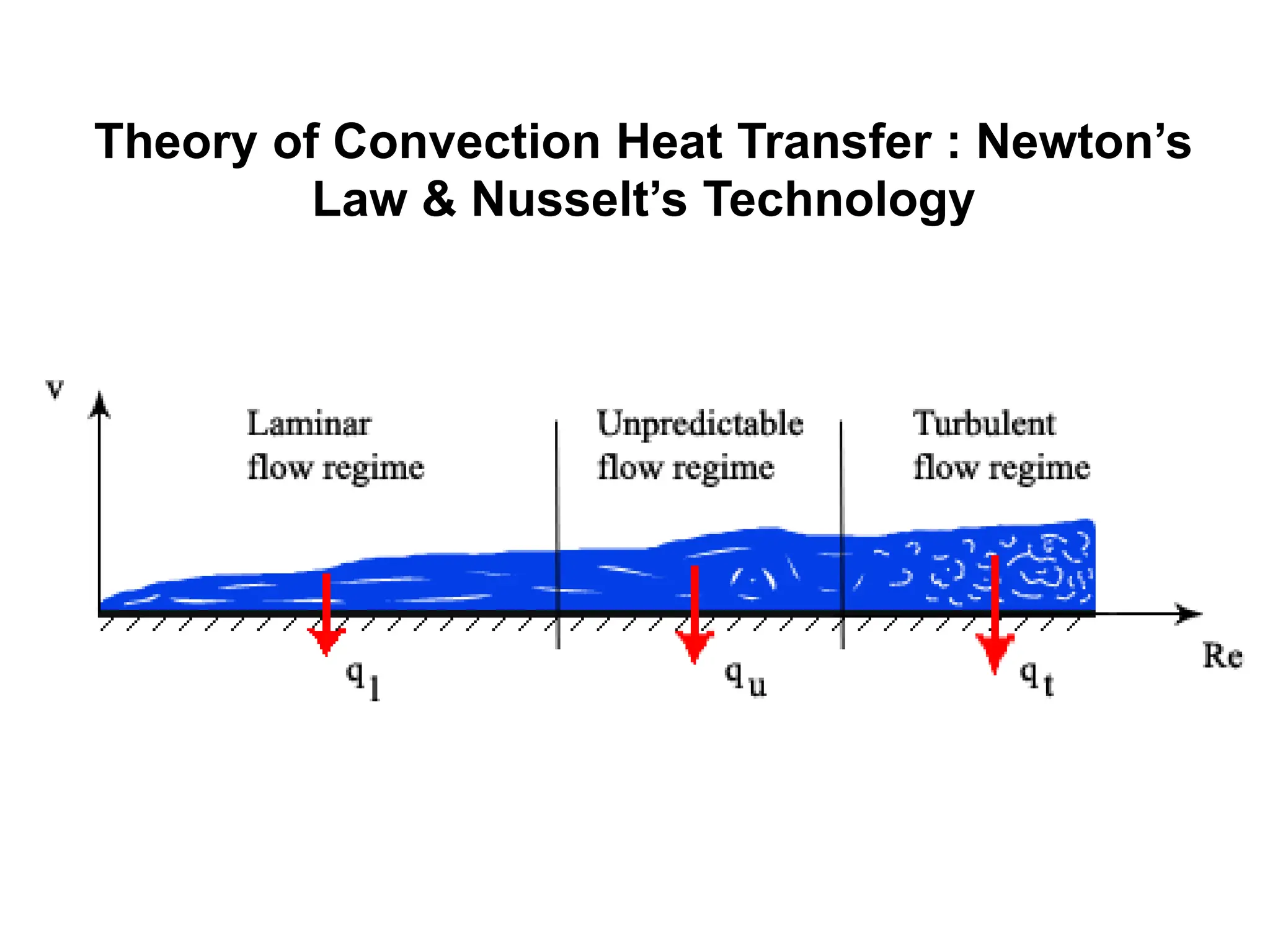
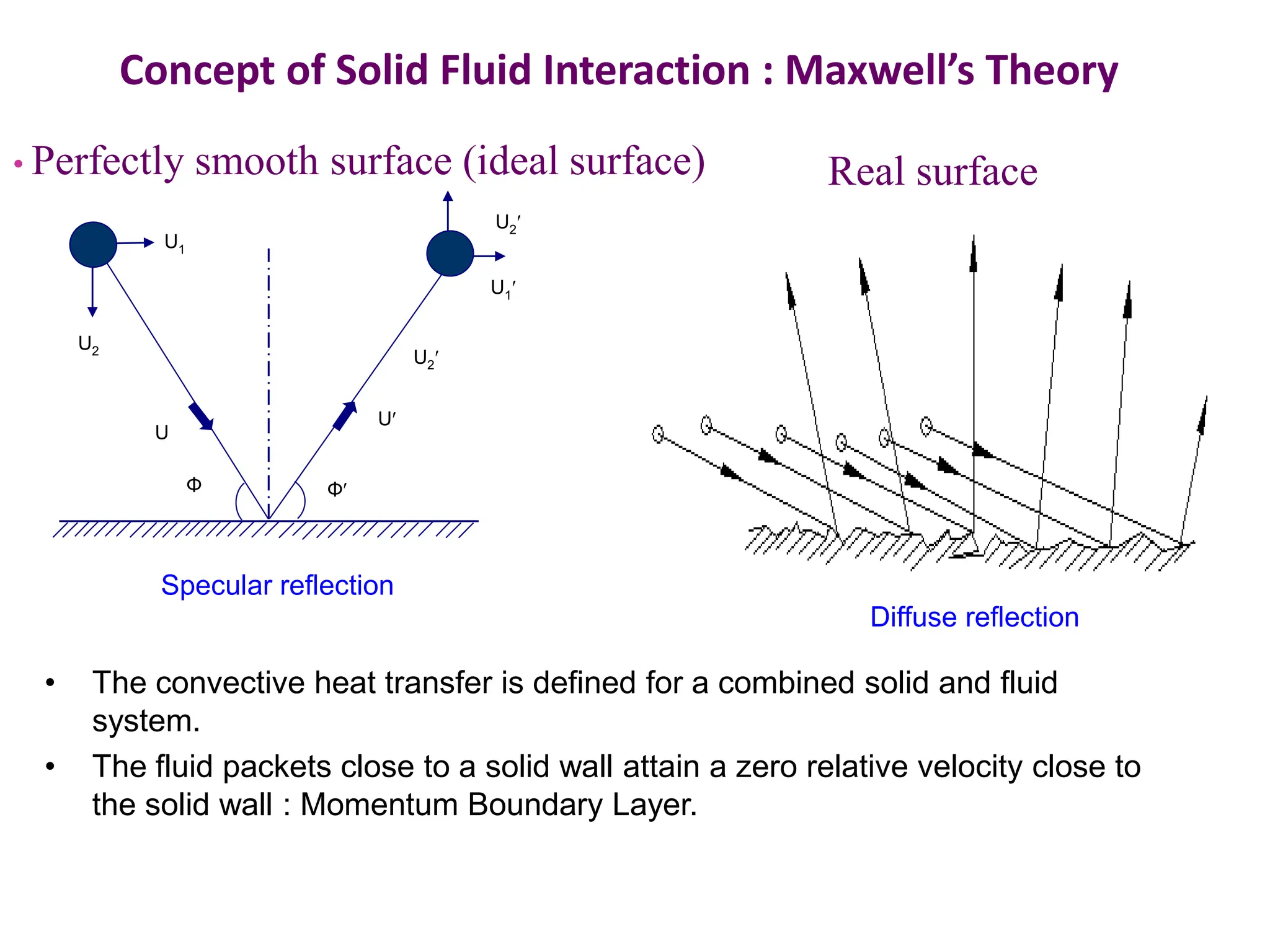
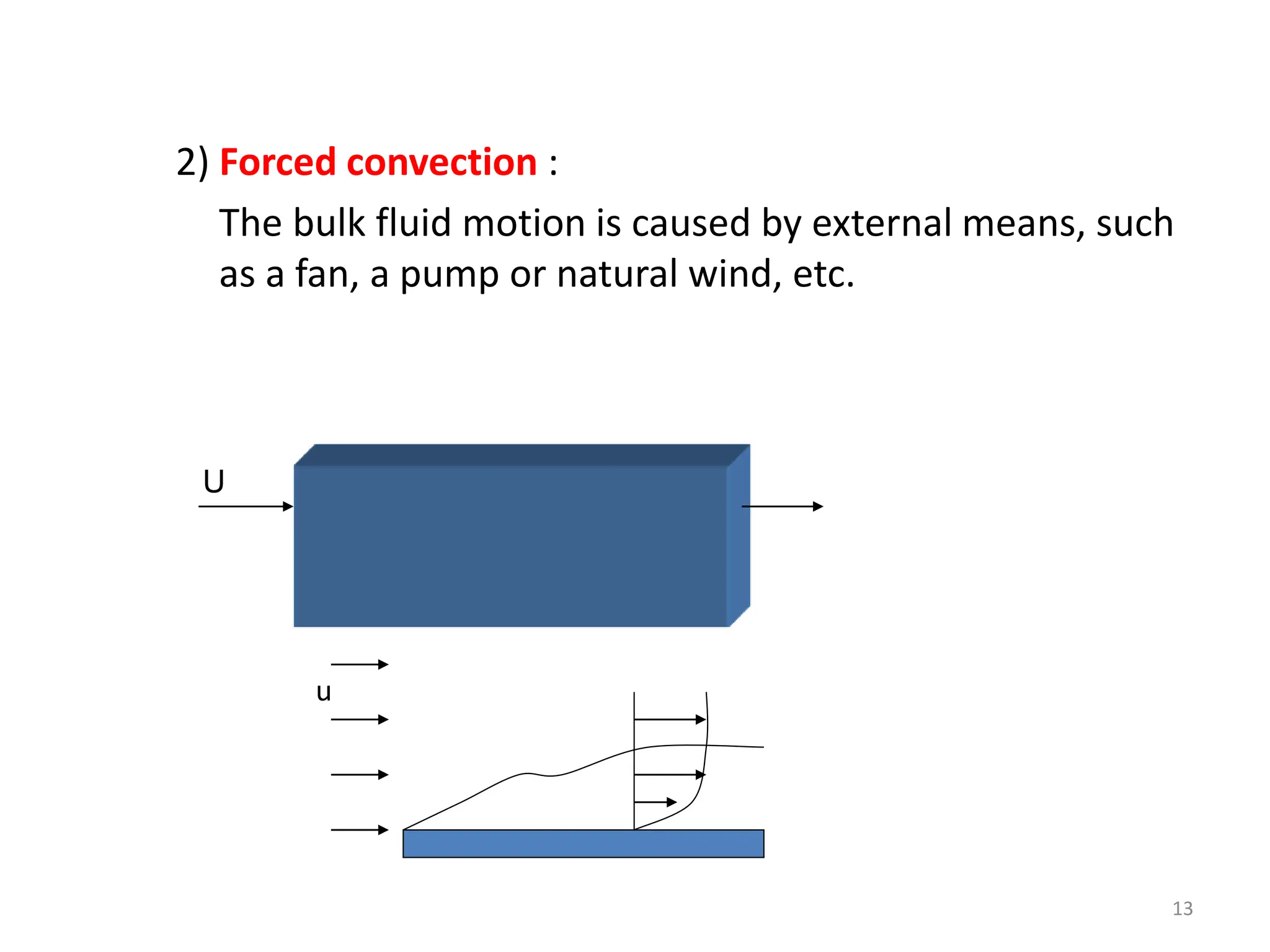
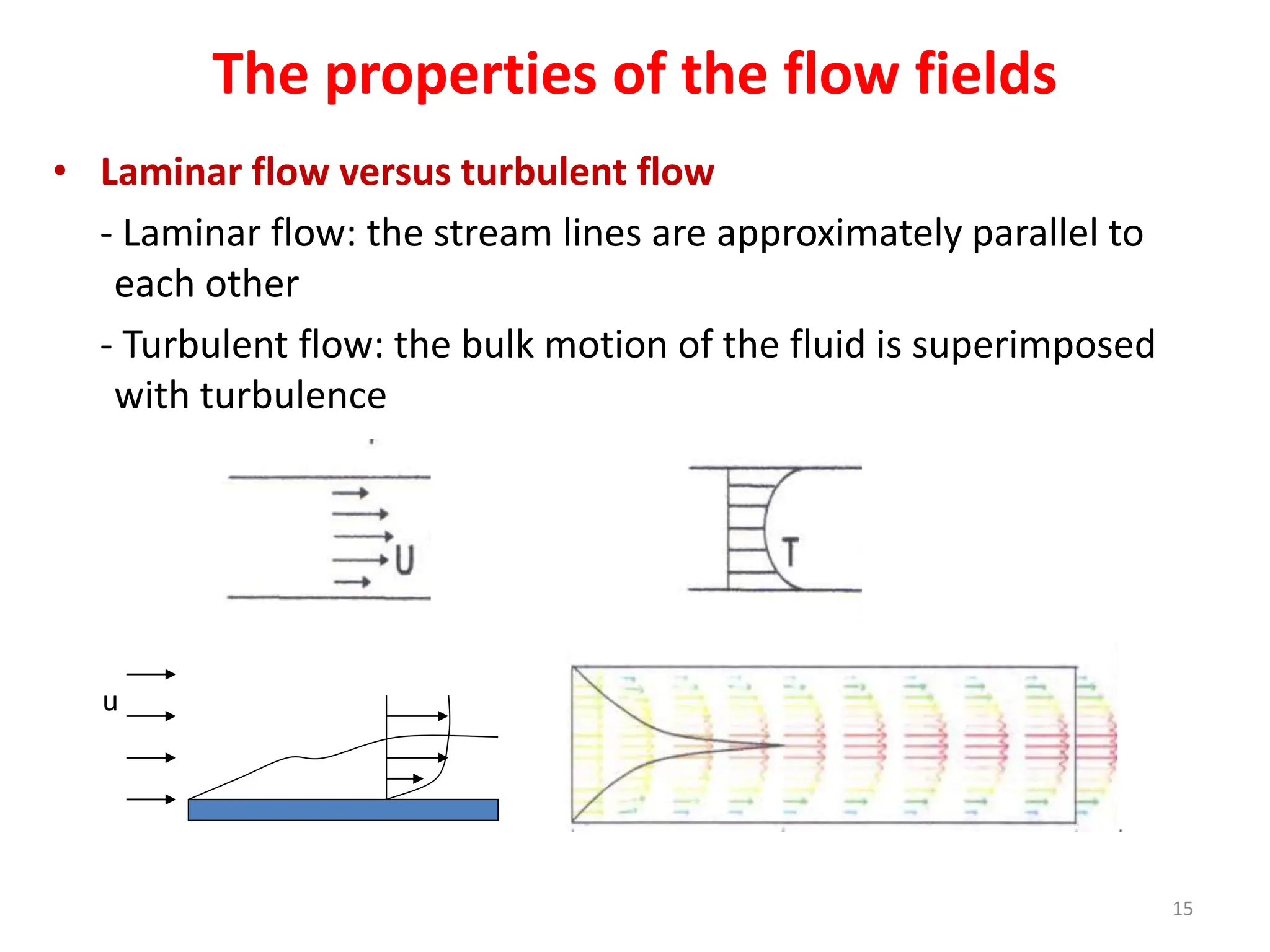
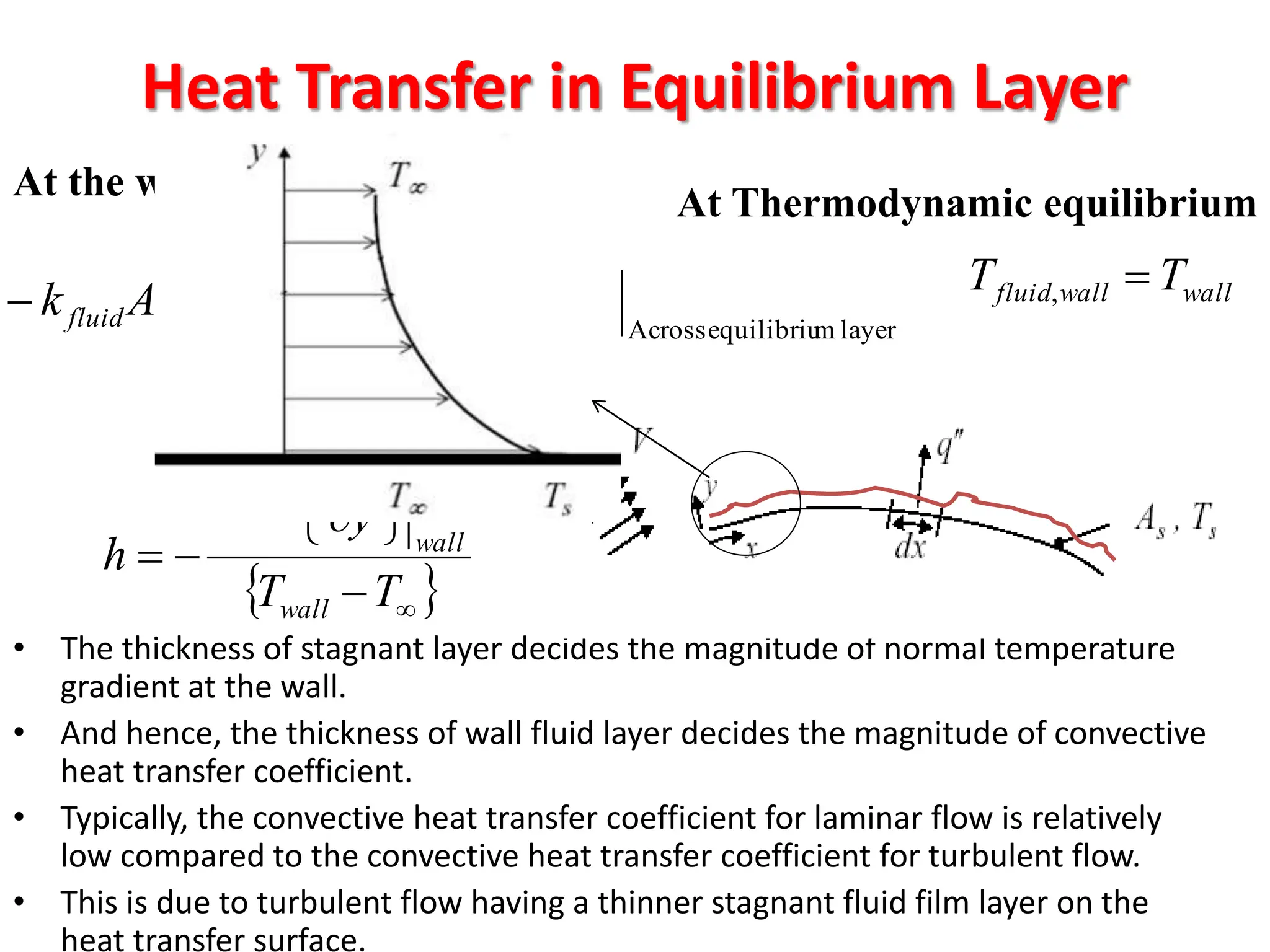
This document provides information about convection heat transfer, including definitions, concepts, governing parameters, and dimensionless numbers used in convection analysis. It defines convection as the mechanism of heat transfer due to bulk fluid motion. Natural and forced convection are described. Dimensionless parameters that characterize convection include the Nusselt number, Reynolds number, Prandtl number, Grashof number, and thermal expansion coefficient. Reducing the governing equations using dimensional analysis is also discussed.

1. Nazaruddin Sinaga
Laboratorium Efisiensi dan Konservasi Energi
Fakultas Teknik Universitas Diponegoro

2. 2
Convection
• Bulk movement of thermal energy in fluids

3. 3
Hot Water Baseboard Heating and
Refrigerators

4. Cold air sinks
Where is the
freezer
compartment put in
a fridge?
Freezer
compartment
It is put at the top,
because cool air
sinks, so it cools the
food on the way
down.
It is warmer at
the bottom, so
this warmer air
rises and a
convection
current is set up.

5. Convection
What happens to the particles in a liquid or a gas when you
heat them?
The particles spread out and become
less dense.
This effects fluid movement.

6. Fluid movement
Cooler, more dense, fluids sink
through warmer, less dense fluids.
In effect, warmer liquids and gases rise up.
Cooler liquids and gases sinks

7. 7
Convection is the process in which heat is carried from
place to place by the bulk movement of a fluid.
Convection currents are set up when a pan of water is
heated.
Convection

8. Why is it windy at the seaside?

9. Theory of Convection Heat Transfer : Newton’s
Law & Nusselt’s Technology

10. Concept of Solid Fluid Interaction : Maxwell’s Theory
Diffuse reflection
U2
U
U
Φ
U2
Φ
U1
U1
Φ
U2
Specular reflection
• Perfectly smooth surface (ideal surface) Real surface
• The convective heat transfer is defined for a combined solid and fluid
system.
• The fluid packets close to a solid wall attain a zero relative velocity close to
the solid wall : Momentum Boundary Layer.

11. • The fluid packets close to a solid wall come to thermal
equilibrium with the wall.
• The fluid particles will exchange maximum possible energy
flux with the solid wall.
• A Zero temperature difference exists between wall and
fluid packets at the wall.
• A small layer of fluid particles close the the wall come to
Mechanical, Thermal and Chemical Equilibrium With solid
wall.
• Fundamentally this fluid layer is in Thermodynamic
Equilibrium with the solid wall.

12. 12
Physical Mechanism of
Convection Heat Transfer
Convection is the mechanism of heat transfer in
the presence of bulk fluid motion.
It can be classified as:
1) Natural or free convection:
The bulk fluid motion is due to buoyant force caused by density
gradient between the hot and cold fluid regions. The temperature &
velocity distributions of free convection along a vertical hot flat
surface is shown in figure below.
Ts
T∞ T∞

13. 13
2) Forced convection :
The bulk fluid motion is caused by external means, such
as a fan, a pump or natural wind, etc.
u
U

14. 14
The properties of the flow fields
• Due to the properties of fluid both velocity and thermal
boundary layers are formed. Velocity boundary layer is
caused by viscosity and thermal boundary layer is
caused by both viscosity and thermal conductivity of the
fluid.
• Internal versus external flow
- External flow : the solid surface is surrounded by the
pool of moving fluid
- Internal flow : the moving fluid is inside a solid channel
or a tube.

15. 15
The properties of the flow fields
• Laminar flow versus turbulent flow
- Laminar flow: the stream lines are approximately parallel to
each other
- Turbulent flow: the bulk motion of the fluid is superimposed
with turbulence
u

16. Heat Transfer in Equilibrium Layer
• The thickness of stagnant layer decides the magnitude of normal temperature
gradient at the wall.
• And hence, the thickness of wall fluid layer decides the magnitude of convective
heat transfer coefficient.
• Typically, the convective heat transfer coefficient for laminar flow is relatively
low compared to the convective heat transfer coefficient for turbulent flow.
• This is due to turbulent flow having a thinner stagnant fluid film layer on the
heat transfer surface.
At the wall for fluid layer :
  layer
m
equilibriu
Across
, 










 T
T
hA
y
T
A
k wall
fluid
fluid
 












T
T
y
T
k
h
wall
wall
fluid
At Thermodynamic equilibrium
wall
wall
fluid T
T 
,

17. Estimation of Heat Transfer
Coefficient
 












T
T
y
T
k
h
wall
wall
fluid

18.  
0
'
'








y
Across
s
y
T
k
T
T
h
q 
Non-dimensional Temperature:





T
T
T
T
s

Non-dimensional length:
L
y
y 
*
0
*
0 *
scale
Length
scale
e
Temperatur















y
y
y
y
T 

19.  
0
*
*










 



y
s
fluid
s
y
L
T
T
k
T
T
h

fluid
y
k
hL
y



0
*
*

0
*
*




y
fluid
y
L
k
h


20. This dimensionless temperature gradient at the wall is named as
Nusselt Number:
resistance
Convection
resistance
Conduction
1



h
k
L
k
hL
Nu
fluid
fluid
fluid
y
k
hL
y
Nu 



0
*
*

Local Nusselt Number

21. Average Nusselt Number
avg
fluid
avg
avg
k
L
h
Nu
,

• Estimation of heat transfer coefficient is basically
computation of temperature profile at the wall.
• A general theoretical and experimental study is
essential to understand how the stagnant layer is
developed.
• The global geometry of the solid wall and flow
conditions will decide the structure of stagnant layer.
• Basic Geometry : Internal Flow or External Flow.

22. 22
The governing parameters of convection
heat transfer
• Newton’s law of cooling
• The main objective to study convection heat transfer is to
determine the proper value of convection heat transfer
coefficient for specified conditions. It depends on the
following parameters:
- The Bulk motion velocity, u, (m/s)
- The dimension of the body, L, ( m)
- The surface temperature, Ts, oC or K
- The bulk fluid temperature, T∞ , oC or K
( )
s
Q hA T T
 

23. 23
The governing parameters of convection
heat transfer (Cont.)
• - The density of the fluid, ρ , kg/m3
- The thermal conductivity of the fluid, kf, (W/m.K)
- The dynamic viscosity of the fluid, μ , (kg/m.s)
- The specific heat of the fluid, Cp , (J/kg.K)
- The change in specific weight, Δ, (kg/(m2s2) or (N/m3)
- The shape and orientation of the body, S
• The convection heat transfer coefficient can be written as
h = f( u, L, Ts, T∞, ρ, kf , μ, Cp, Δ , S)

24. 24
• It is impossible to achieve a correlation equation for
convection heat transfer in terms of 10 variables. A better
way to reduce the number of variables is required.
• Dimensionless analysis
There are 11 parameters with 4 basic units (length, m), (mass,
kg), (temperature, oC or K) , and (time, s).
Applying the method of dimensional analysis, it can be
grouped into 11- 4 = 7 dimensionless groups, they are:
3 2
2
( , , , , , )
p s
p
c T
hL uL g L u
F S
k k T c T

  
   



25. 25
1. Nusselt number : =
2. Eckert number : =
3. Reynods number : =
4. Temperature ratio : θs =
5. Grashof number : =
6. S : shape of the surface
7. Prandtl number : =
hL
k
uL


3
2
g L
 


p
c
k

2
p
u
c T
s
T
T
L
Nu
ReL
L
Gr
Pr
k
E

26. 26
The Governing Parameters of
Convection Heat Transfer
• The convection heat transfer
coefficient can be written as:
Nu = f( Ek , ReL, θs , GrL , Pr, S)

27. 27
• To find Reynolds number
Choosing density (ρ), dimension (L), surface temperature (Ts), and
dynamic viscosity (μ) as the 4 basic parameters, and velocity (u) as the
input parameter. The dimensionless number is obtained by solving the 4
constants, a, b, c, & d.
1
3
0
( ) ( ) ( ) ( )
3 1 0
0
0
1 0
1, 0, 1, 1
Re
a b c d
s
a b o c d
o
L
L T u
kg kg L
L C
L sL s
L a b d
kg a d
C c
s d
d c a b
Lu
 






     
  
 
   
    
 

28. 28
Simply the dimensionless equations !!!
 Now we have reduced the equation involving 11
variables into a 7 dimensionless group equation.
 However, 7 dimensionless groups is still too large, we
need neglecting the unimportant dimensionless
groups.
 Eckert number is important for high speed flow. It can be
neglected for our application.
 If the average fluid temperature is used for getting the fluid
properties, the temperature ratio can also be discarded.

29. 29
Nu = f( Ek , ReL, θs , GrL , Pr, S)
After neglecting the two unimportant
dimensionless groups, the general
convection equation is
(Re ,Pr, , )
L L L
Nu F Gr S


30. 30
• Forced Convection: the density change is very small, the
Grashoff number is neglected
• Natural Convection: there is no bulk fluid motion induced by
external means, u = 0, Reynolds number is disappeared.
(Re ,Pr, )
L L
Nu F S

( ,Pr, )
L L
Nu F Gr S


31. 31
The Physical Meaning of
The Dimensionless Numbers
• Nusselt Number
It is the ratio of convection heat transfer
rate to the conduction heat transfer rate.
Consider an internal flow in a channel of
height L and the temperatures at the lower
and upper surfaces are T1 & T2, respectively.
The convection heat transfer rate is
The conduction heat transfer rate is
The ratio
&
Qcov
 hA(T1
T2
)
&
Qcond

kA
L
(T1
 T2
)
NuL

&
Qcov
&
Qcond

hA
kA
L

hL
k
u
T1
T2
L

32. 32
• The Reynolds Number
It is the ratio of inertia force to viscous force of the
moving fluid.
- Inertia force
- The viscous force
- The ratio
3 2 2 2 2
2
( )
i
L L
F ma L L L u
s s
  
   
2 2
v
u u
F A L L uL
y L
   

   

ReL
uL uL uL


 

  

33. 33
• The Prandtl Number
 It is the ratio of the momentum diffusivity to the thermal
diffusivity.
 The momentum diffusivity is the kinematic viscosity and it
controls the rate of diffusion of momentum in a fluid
medium.
 Thermal difusivity controls how fast the heat diffuses in a
medium. It has the form
The ratio of the two is called Prandtl number.
Pr
p
p
c
k k
c


 


  
p
k
c




34. 34
• The Thermal Expansion Coefficient
It is defined as
The negative sign results from the fact that, for gases, the
change of density with respect to temperature under constant
pressure process is always negative. From ideal gas law
For ideal gas, the thermal expansion coefficient is the inverse
of the absolute temperature
1
( )p
T




 

0
p RT dp RdT RTd
  
     ( )p
d
dT T
 
 
1
T
 

35. 35
• Grashoff Number
The Grashoff number represents the ratio of
the buoyant force to the viscous force.
3
2
g L
Gr

 



36. 36
• Grashof number
The change of density is
Substituting into Grashof number
The subscript L means that the characteristic length of the
Grashof number. It may be the length of the surface. For
ideal gas, GrL is
( ) ( )
T T T T T
     
  
          
3 3
3
2 2 2
( ) ( )
L
g T T L g T T L
g L
Gr
 

    
 
 

  
3
2
( )
L
g T T L
Gr
T




Ts
T∞ T∞
Buoyant force
Viscous force

37. Chapter 1 Chee 318 37
Example
Air at 20°C blows over a hot plate, which is maintained at
a temperature Ts=300°C and has dimensions 20x40 cm.
C
T 
20


q”
C
TS

300

Air
The convective heat flux is proportional to


 T
T
q S
x
"

38. Chapter 1 Chee 318 38
• The proportionality constant is the convection heat
transfer coefficient, h (W/m2.K)
)
(
"


 T
T
h
q S
x Newton’s law of Cooling
• For air h=25 W/m2.K, therefore the heat flux is qx”= 7,000
W/m2
• The heat rate, is qx= qx”. A = qx”. (0.2 x 0.4) = 560 W.
• In this solution we assumed that heat flux is positive when heat
is transferred from the surface to the fluid
• How would this value change if instead of blowing air we had
still air (h=5 W/m2.K) or flowing water (h=50 W/m2.K)

39. The End
Terima kasih