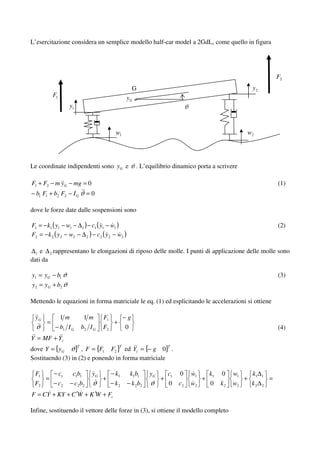
Il documento descrive la simulazione di un modello dinamico half-car a 2 gradi di libertà per un veicolo, evidenziando le equazioni che governano il comportamento dinamico e l'equilibrio del sistema. Viene presentato un approccio numerico per risolvere il sistema di equazioni differenziali e si discute l'impatto di un dosso sul comportamento dell'auto. Infine, si menzionano i parametri di progetto e le caratteristiche delle sospensioni da ottimizzare per migliorare le prestazioni del veicolo.

1. Simulazione tramite un programma in Matlab di un semplice modello dinamico di tipo half-
car model a 2 gradi di libertà.
Un automobile è un sistema dinamico complesso. Il corpo principale dell’automobile (vedi figura
seguente) ha 6 GdL. A questi vanno aggiunti i gradi di libertà dovuti agli spostamenti relativi delle
altre masse all’interno del veicolo come motore, assi, ruote, sedili + passeggeri.
Per ottimizzare la scelta dei componenti costituenti le sospensioni sono stati proposti durante gli
anni diversi modelli di cui si è studiato il comportamento dinamico, mettendo in evidenza di volta
in volta caratteristiche dinamiche diverse. Sostanzialmente i tipi di modelli si dividono in due
grandi raggruppamenti: half-car model ed quarter-car model. I primi considerano il comportamento
dinamico di “mezza auto”, supponendo che vi sia simmetria tra parte destra e parte sinistra. I
secondi considerano solo un quarto di auto focalizzando lo studio su di una sola sospensione senza
tenere conto delle reciproche influenze tra le sospensioni di più ruote.
In seguito è riportato uno schema di un half-car model. Il sistema ha 5 GdL: rotazione e posizione
verticale del corpo centrale; posizioni delle due ruote; posizione del sedile dell’autista.
Anche il modello seguente appartiene ad i half-car model. Rispetto al precedente, ha 1 GdL in
meno, in quanto non viene considerata la posizione del sedile dell’autista. Inoltre non si tiene conto
dello smorzamento del pneumatico. Notare che in mezzo tra smorzatore e molla c’è un elemento
aggiuntivo che rappresenta una sospensione attiva (attuatore).

2. Per ultimo presentiamo il modello di un quarter-car. (2 GdL) E’ presente solo un quarto della massa
dell’automobile e la massa della ruota + l’asse della ruota.

3. L’esercitazione considera un semplice modello half-car model a 2GdL, come quello in figura
F2
G y2
F1 yG
y1 ϑ
w1 w2
Le coordinate indipendenti sono yG e ϑ . L’equilibrio dinamico porta a scrivere
F1 + F2 − m yG − mg = 0 (1)
− b1 F1 + b2 F2 − I G ϑ = 0
dove le forze date dalle sospensioni sono
F1 = −k1 ( y1 − w1 − ∆1 ) − c1 ( y1 − w1 ) (2)
F2 = −k 2 ( y 2 − w2 − ∆ 2 ) − c2 ( y2 − w2 )
∆1 e ∆ 2 rappresentano le elongazioni di riposo delle molle. I punti di applicazione delle molle sono
dati da
y1 = yG − b1 ϑ (3)
y 2 = yG + b2 ϑ
Mettendo le equazioni in forma matriciale le eq. (1) ed esplicitando le accelerazioni si ottiene
yG 1m 1m F1 −g
= +
ϑ − b1 I G b2 I G F2 0 (4)
Y = MF + Yc
dove Y = {yG ϑ} , F = {F1 F2 } ed Yc = {− g 0} .
T T T
Sostituendo (3) in (2) e ponendo in forma matriciale
F1 − c1 c1b1 yG − k1 k1b1 yG c1 0 w1 k 0 w1 k∆
= + + + 1 + 1 1 =
F2 − c2 − c2b2 ϑ − k2 − k 2 b2 ϑ 0 c2 w2 0 k2 w2 k2∆ 2
F = CY + KY + C ′W + K ′W + Fc
Infine, sostituendo il vettore delle forze in (3), si ottiene il modello completo

4. Y = M (CY + KY + C ′W + K ′W + Fc ) + Yc =
(5)
= MCY + MKY + MC ′W + MK ′W + MFc + Yc
Notare che le matrici MC, MK, MC’, MK’ ed MFc sono costanti e note. Perciò il sistema di
equazioni dinamiche (5) fornisce l’accelerazione del vettore delle coordinate indipendenti a partire
da velocità e posizione del vettore delle coordinate indipendenti
Y Modello
dinamico
Y 2 equazioni
Y
W
W
velocità e posizione del vettore che definisce il punto di appoggio delle ruote.
Per risolvere il sistema di equazioni differenziali è sufficiente ricorrere ai metodi tradizionali di
soluzione, dato che ci troviamo di fronte ad eq. differenziali a coefficienti costanti.
In alternativa, si imposterà un metodo numerico di soluzione. Il metodo è un metodo iterativo.
Conoscendo il vettore velocità ad un certo istante i-esimo, la velocità ad un istante i+1-esimo può
essere stimata attraverso la seguente relazione
Yi+1 = Yi + Yi +1 dt (6)
dove dt è l’incremento temporale tra un istante e l’altro. Vale la stessa cosa per il vettore posizione,
perciò
Yi +1 = Yi + Yi +1 dt (7)
In uno schema iterativo, partendo dalla conoscenza del vettore velocità e posizione al passo i-esimo,
attraverso la formula (5) è possibile calcolare il vettore accelerazione al passo i+1-esimo.
Successivamente, attraverso le formule (6) e (7) si stimano velocità ed accelerazioni al passo i+1-
esimo. Il ciclo riparte, ricalcolando l’accelerazione al passo i+2-esimo sempre con la formula (5).
Quanto detto è schematizzato nel seguente schema a blocchi
Yi Modello
dinamico Stima Stima
Yi 2 equazioni Yi+1 velocità Yi +1 Yi +1
posizione
Wi
Wi
Aggiornamento
di Yi e Yi

5. Scelta delle condizioni iniziali
Dato che il metodo è iterativo, è necessario individuare due valori di partenza per il vettore velocità
e posizione. Si può ipotizzare che l’automobile stia percorrendo all’inizio un tratto rettilineo su una
superficie idealmente piana. Perciò l’auto in questa fase iniziale non subisce sobbalzi, perciò il
vettore velocità è nullo, cioè
{
Y0 = yG 0 ϑ0 } = {0 0}
T T
(8)
Il vettore posizione al contrario non è nullo, perché le molle devono essere compresse di una
determinata quantità per bilanciare la forza peso, anche se si sta percorrendo un tratto rettilineo
piano. La posizione iniziale si determina risolvendo l’equazione (5), nel caso in cui accelerazioni e
velocità del corpo rigido siano nulle (moto a regime) e non vi sia alcuna sollecitazione dal terreno
( W = W = 0 ). Perciò
0 = MKY + MFc + Yc
(9)
Y0 = −(MK ) MFc − (MK ) Yc
−1 −1
Tipologia della forzante
Bisogna tradurre le caratteristiche del terreno attraverso la definizione dei vettori W e W nel tempo.
Poniamoci come obiettivo lo studio del comportamento dinamico dell’automobile quando incontra
un dosso.
h
l s
La prima ruota dell’auto incontra il dosso dopo una distanza l; il dosso è alto h ed è lungo s.
Rappresentiamo il dosso attraverso una funzione sinusoidale, perciò l’andamento del terreno può
essere espresso dalla funzione
0 se x<l
h 2π
hx ( x ) = 1 − cos (x − l ) se l ≤ x < l + s (10)
2 s
0 se x ≥ l + s
La simulazione deve essere eseguita ad una ben determinata velocità dell’automobile v. Per cui lo
spostamento del punto di appoggio della prima ruota che va incontro al dosso è espresso rispetto al
tempo da
x = vt
Sostituendo nella eq. (10), si ottiene

6. 0 se t < l v
h 2π
w1 (t ) = 1 − cos (v t − l ) se l v ≤ t < (l + s ) v (11)
2 s
0 se t ≥ (l + s ) v
La seconda ruota impatta il dosso con un determinato ritardo, dato da
t r = (b1 + b1 ) v
Perciò l’andamento del punto di appoggio della seconda ruota è
0 se t < l v + t r
h 2π
w2 (t ) = 1 − cos (v t − l − t r ) se l v + t r ≤ t < (l + s ) v + t r (12)
2 s
0 se t ≥ (l + s ) v + t r
Conoscendo l’andamento temporale dei punti di appoggio delle ruote rispetto al tempo si possono
calcolare anche le velocità
0 se t < l v
π hv 2π
w1 (t ) = sin (v t − l ) se l v ≤ t < (l + s ) v (13)
s s
0 se t ≥ (l + s ) v
0 se t < l v + t r
π hv 2 pi
w2 (t ) = sin (v t − l − t r ) se l v + t r ≤ t < (l + s ) v + t r (14)
s s
0 se t ≥ (l + s ) v + t r
Supponiamo che l’incremento temporale scelto sia dt. I vettori che esprimono le posizioni e le
velocità dei punti di appoggio sono
w1 (i dt )
Wi =
w2 (i dt )
(15)
w1 (i dt )
Wi =
w2 (i dt )
Notare che nelle ultime equazioni il simbolo “i” non indica un valore complesso, bensì un numero
naturale.

7. Modello ottimizzato delle sospensioni
Nel modello precedente si ipotizza che le ruote non si distacchino mai dal terreno. Se si vuole
introdurre un modello più raffinato è necessario tenere conto del distacco, durante il quale le forze
esercitate dalle sospensioni non diventano mai negative. Per imporre che le forze non diventino
negative bisogna modificare l’eq. che esprime le forze
F1 se F1 > 0 F2 se F2 > 0
F1r = F2 r =
0 se F1 ≤ 0 0 se F2 ≤ 0
dove F1r ed F2 r sono le forze del modello con distacco delle ruote.
Note riguardanti l’implementazione
Dati caratteristici dell’auto:
m = 630 kg; I G = 840 kgm2; b1 = 1.56 m; b2 = 2.84 m;
Dati riguardanti la simulazione:
v = 70 km/h; l = 0.1 m; s = 0.3 m; h = 0.1 m;
Per quanto riguarda le sospensioni devono essere inserite diverse combinazioni in maniera da
determinare l’assetto ottimale dell’automobile (le rigidezze sono dell’ordine di grandezza delle
decine/centinaia di migliaia di N/m; gli smorzamenti sono dell’ordine di grandezza di migliaia
Ns/m).