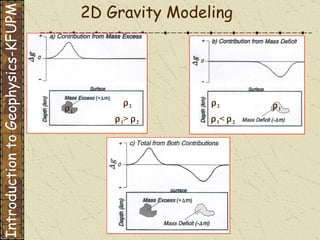
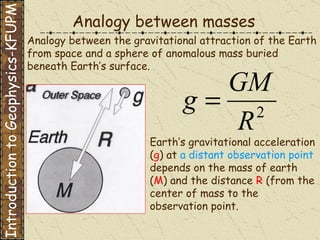
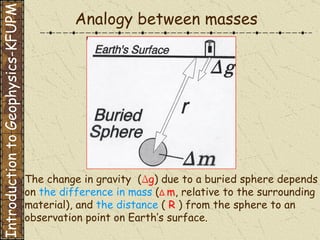
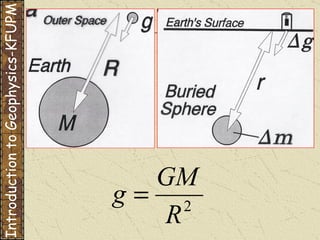
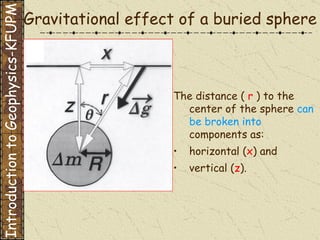
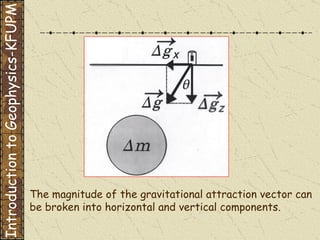
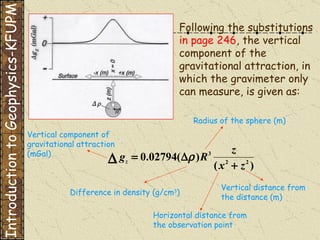
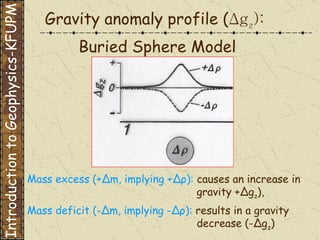
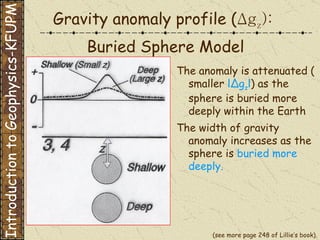
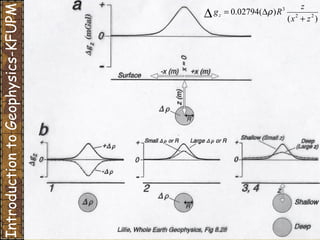
The document discusses gravity modeling and introduces the buried sphere model. It explains that a buried sphere of different density than the surrounding material causes a gravitational anomaly that can be measured on Earth's surface. The vertical component of this gravitational attraction depends on the density difference of the sphere, its radius, and the horizontal and vertical distances from the observation point. A more massive sphere or one closer to the surface produces a larger anomaly. Deeper spheres cause smaller, wider anomalies.

1. Ali Oncel [email_address] Department of Earth Sciences KFUPM Gravity Modeling 2 Introduction to Geophysics Introduction to Geophysics-KFUPM Highest peaks on the planet

2. Previous Lecture Local Isostasy & Flexure Regional Isostasy & Flexure Flexural Rigidity (D) Flexural Modeling Examples of Lithospheric Flexure Example from the West Africa (Watts and Stewart, 1998). Introduction to Geophysics-KFUPM

3. Homework Status, Due to May 17 Use the online tool for making a gravity map from the site http://www.itis-molinari.mi.it/Gravity.htm . Make your gravity map and compare changes in the gravity to changes through regions of major tectonics? What is the gravity through the areas: a) Red Sea b) Dead Sea Fault c) Iranian Sea d) Gulf of Aqaba e) Zagros Thrust Fold Introduction to Geophysics-KFUPM

4. Introduction to Geophysics-KFUPM

5. Red Sea Arabian Gulf DSF Arabian Shield Gulf of Aden Zagros Suture GO AS MS OM Introduction to Geophysics-KFUPM

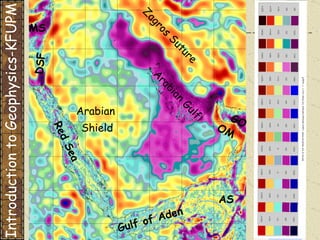
6. Homework Status, Due to May 20 Given the following exercises of your handout: 8.2 8.3 8.8 Try to use one of those provided Excel Programs if possible in solving your problems from the link: http://www.mtech.edu/clink/Home/Classes/Geop3020/chapter6.htm Then, e-mail your homework which is solved under Excel to me : [email_address] . Introduction to Geophysics-KFUPM

7. 2D Gravity Modeling  1 >  2  1  2  1 <  2  1  2 Introduction to Geophysics-KFUPM

8. Analogy between the gravitational attraction of the Earth from space and a sphere of anomalous mass buried beneath Earth’s surface. Earth’s gravitational acceleration ( g ) at a distant observation point depends on the mass of earth ( M ) and the distance R (from the center of mass to the observation point. Analogy between masses Introduction to Geophysics-KFUPM

9. The change in gravity ( Δ g ) due to a buried sphere depends on the difference in mass ( Δ m , relative to the surrounding material), and the distance ( R ) from the sphere to an observation point on Earth’s surface. Analogy between masses Introduction to Geophysics-KFUPM

10. Introduction to Geophysics-KFUPM

11. Gravitational effect of a buried sphere The distance ( r ) to the center of the sphere can be broken into components as: horizontal ( x ) and vertical ( z ). Introduction to Geophysics-KFUPM

12. The magnitude of the gravitational attraction vector can be broken into horizontal and vertical components. Introduction to Geophysics-KFUPM

13. Introduction to Geophysics-KFUPM See pages 245-246 to see how that equation is derived since final equation is given here as: Horizontal component Vertical component

14. Following the substitutions in page 246 , the vertical component of the gravitational attraction, in which the gravimeter only can measure, is given as: Vertical component of gravitational attraction (mGal) Difference in density (g/cm 3 ) Radius of the sphere (m) Horizontal distance from the observation point Vertical distance from the distance (m) Introduction to Geophysics-KFUPM

15. Gravity anomaly profile ( Δ g z ): Buried Sphere Model Mass excess (+ Δ m, implying + Δ ρ ): causes an increase in gravity + Δ g z ), Mass deficit (- Δ m, implying - Δ ρ ): results in a gravity decrease ( - Δ g z ) Introduction to Geophysics-KFUPM

16. The more massive the sphere (larger Δ ρ /or larger R), the greater the amplitude ( l - Δ g z l ) of the gravity anomaly Gravity anomaly profile ( Δ g z ): Buried Sphere Model Introduction to Geophysics-KFUPM

17. The anomaly is attenuated ( smaller l Δ g z l ) as the sphere is buried more deeply within the Earth The width of gravity anomaly increases as the sphere is buried more deeply. Gravity anomaly profile ( Δ g z ): Buried Sphere Model Introduction to Geophysics-KFUPM (see more page 248 of Lillie’s book).

18. Introduction to Geophysics-KFUPM