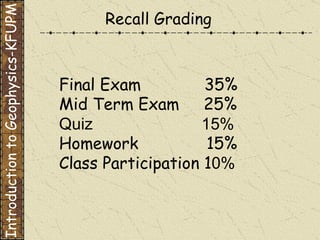
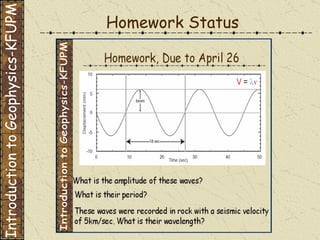
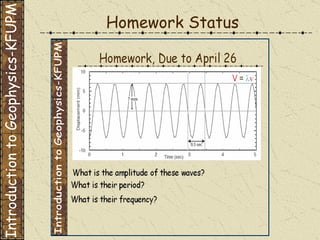
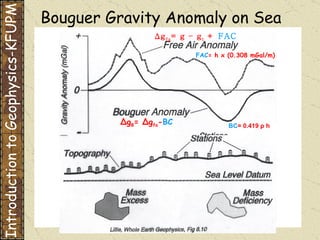
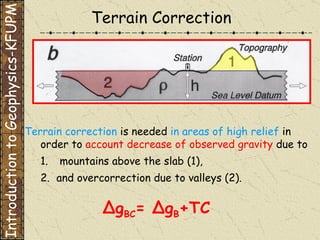
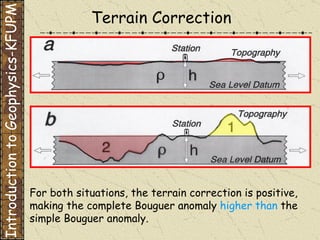
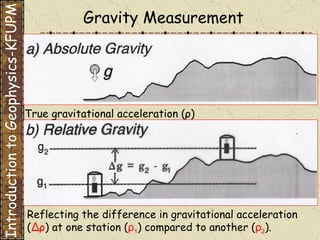
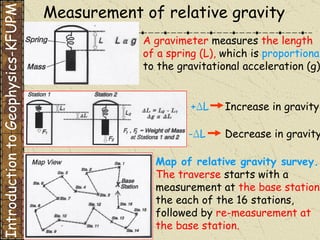
The document discusses gravity methods in geophysics. It provides examples of gravity measurements and calculations, including Bouguer corrections on land and sea. It also discusses different units used to measure gravitational acceleration and explains the use of milligals for small measurements like on Phobos.

1. Ali Oncel [email_address] Department of Earth Sciences KFUPM Gravity Methods 3 Introduction to Geophysics Introduction to Geophysics-KFUPM

2. Previous Lecture Gravity Methods 2 Bouguer Correction Bouguer Gravity Anomaly on Land Bouguer Gravity Anomaly on Sea Mid-Term Exam Introduction to Geophysics-KFUPM

3. Grade Students Grade Distribution in Mid-Term Exam 204317 214269 222736 226202 234345 Introduction to Geophysics-KFUPM

4. Mid-Term Exam Solutions h 1 X CR h 1 V 1 V 2 1200 3200 0.4 0.6 Meters Seconds V 1 , V 2 , h 1 ? 0.3 0.2 0.1 Introduction to Geophysics-KFUPM Simplified version of Assignment 2

5. Introduction to Geophysics-KFUPM For example, a double spike function , 2, 0, 1 convolved with an impulse response function 4, 3, 2, 1 . It was class example of Lecture 9.2 From Kearey, Brooks, and Hill, 2002

6. Given that the P-velocity of a rock is 6.8 km/s, the S-velocity is 3.82 km/s, and density 2.95 g/cm 3 , calculate µ and k? Introduction to Geophysics-KFUPM Modified version asked in Quiz 1

7. Where possible, supply the missing quantity in each case in the following table, where: i = angle of incidence r = angle of refraction v1 = wave speed in upper layer, v2 = wave speed in lower layer. The wave originates in the upper layer. Introduction to Geophysics-KFUPM Modified version asked in Quiz 2

8. The same question solved in Class v 1 =1500 m s -1 v 2 =2000 m s -1 v 3 =2345 m s -1 t 1 =2.14 s t 2 =1.21 s t 3 =1.13 s v rms at the base of layer 3? Introduction to Geophysics-KFUPM v rms at the base of layer 1? v rms at the base of layer 2?

9. Introduction to Geophysics-KFUPM

10. Introduction to Geophysics-KFUPM

11. Introduction to Geophysics-KFUPM

12. Recall Grading Introduction to Geophysics-KFUPM

13. Homework Status Introduction to Geophysics-KFUPM

14. Homework Status Introduction to Geophysics-KFUPM

15. Homework Status Introduction to Geophysics-KFUPM

16. Summary of Equations for Free Air and Bouguer Gravity Anomalies Standard parameters used to compute gravity anomalies on land and at sea. FAC =Free-Air Correction; BC =Bouguer Corrections; BC s =Bouguer correction at sea ρ =reduction density; h =elevation (m) and hw =water depth (m) Introduction to Geophysics-KFUPM

17. Bouguer Gravity Anomaly on Sea Introduction to Geophysics-KFUPM Δ g fa = g – g t + FAC Δ g B = Δ g fa - BC BC = 0.419 ρ h FAC = h x (0.308 mGal/m)

18. Terrain Correction Introduction to Geophysics-KFUPM Δ g BC = Δ g B +TC terrain correction is no needed in areas of low relief but is required where changes in topography is significant and equation for a complete Bouguer anomaly is:

19. Terrain correction is needed in areas of high relief in order to account decrease of observed gravity due to mountains above the slab (1), and overcorrection due to valleys (2). Terrain Correction Introduction to Geophysics-KFUPM Δ g BC = Δ g B +TC

20. Terrain Correction For both situations, the terrain correction is positive, making the complete Bouguer anomaly higher than the simple Bouguer anomaly. Introduction to Geophysics-KFUPM

21. Gravity Measurement Introduction to Geophysics-KFUPM True gravitational acceleration ( ρ ) Reflecting the difference in gravitational acceleration ( Δρ ) at one station ( ρ 1 ) compared to another ( ρ 2 ).

22. Measurement of relative gravity A gravimeter measures the length of a spring (L), which is proportional to the gravitational acceleration (g). + Δ L Increase in gravity - Δ L Decrease in gravity Map of relative gravity survey. The traverse starts with a measurement at the base station , the each of the 16 stations, followed by re-measurement at the base station. Introduction to Geophysics-KFUPM

23. Microgravity surveys require that we measure g with precision of better than 1 part in 40 million • we measure either absolute gravity or more commonly, relative gravity ( change in g between two stations ) Methods: 1. Falling body 2. Pendulums 3. Mass-spring gravimeters Gravity Measurement Introduction to Geophysics-KFUPM

24. Gravitational acceleration can be measured directly by dropping an object and measuring its acceleration. Free Fall Methods • distance a body falls is proportional to the time it has fallen squared z = ½ g t 2 g = 2 z /t 2 g inst = 2 ·50 m/(3.19 s) 2 = 9.8 m/s 2 Introduction to Geophysics-KFUPM

25. Pendulums Gravity first measured by Pierre Bouguer in 1749 ( 257 years ago ) using Pendulum: period of oscillation T of pendulum is inversely proportional to g T = 2  K /g K = constant related to pendulum design Introduction to Geophysics-KFUPM

26. Gravity Units Most of us are familiar with the units of g as feet/sec 2 or meters/sec 2 , etc. From Newton’s law of gravity g also has units of Introduction to Geophysics-KFUPM

27. Using the metric system, we usually think of g as being 9.8 meters/sec 2 . This is an easy number to recall. If, however, we were on the Martian moon Phobos, g p is only about 0.0056meters/sec 2 [m/sec 2 ] might not be the most useful units to use on Phobos. Some unit names you will hear when gravity applications are discussed include: 9.8 m/sec 2 980 Gals (or cm/sec 2 ) 980000 milligals (i.e. 1000th of a Gal) We experience similar problems in geological applications, because changes of g associated with subsurface density contrasts can be quite small . Gravity Units http://www.esa.int/SPECIALS/Mars_Express/SEM21TVJD1E_0.html Introduction to Geophysics-KFUPM

28. 1 mGal = 10 microns/sec 2 1 milligal equals 10 -5 m/sec 2 or conversely 1 m/sec 2 = 10 5 milligals. The gravity on Phobos is 0.0056m/s 2 or 560 milligals . Are such small accelerations worth contemplating? Can they even be measured? Gal Gal = 1 cm/sec 2 = 0.01 m/sec 2 1 mGal = 10 -3 Gal Istituto e Museo di Storia della Scienza Introduction to Geophysics-KFUPM 1564-1642