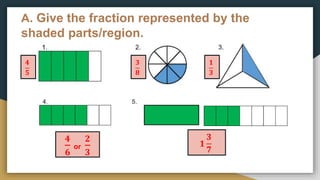
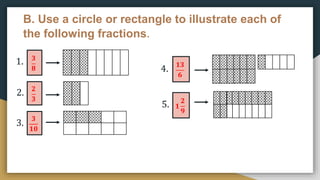
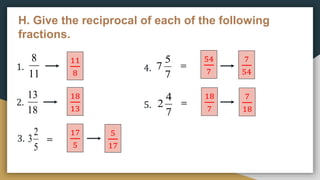
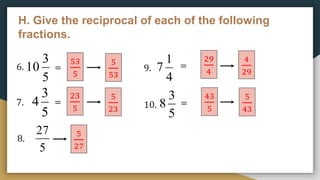
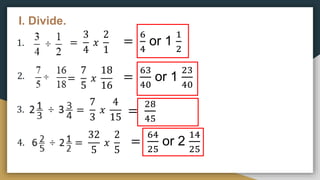
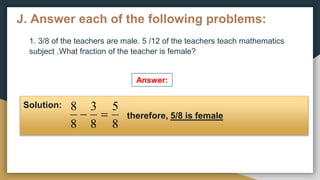
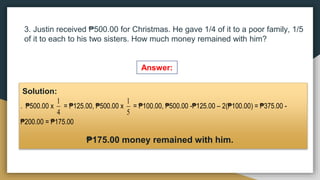
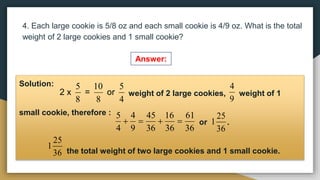
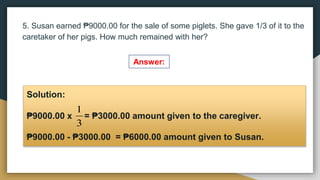
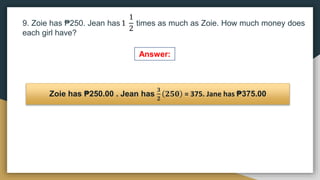
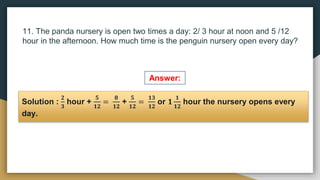
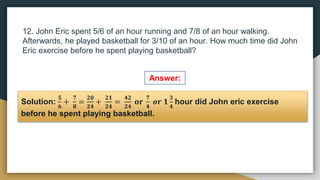
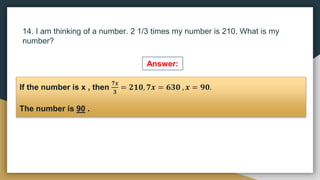
1) The document provides examples and exercises on fractions, including representing fractions, comparing fractions, reducing fractions to lowest terms, and operations involving fractions such as addition, subtraction, multiplication, division, and solving word problems involving fractions. 2) The problems cover a range of skills and concepts related to fractions including illustrating fractions using circles or rectangles, arranging fractions in order from least to greatest or greatest to least, reducing fractions, performing the basic operations on fractions, and solving multi-step word problems involving fractions. 3) The document is intended for a 5th grade mathematics session, with the goal of reinforcing students' understanding of key fraction concepts and skills through worked examples and practice exercises.

1. MTAP Program of
Excellence in Mathematics
Grade 5 Session 3
LUIS V. SALENGA
(Teacher )

3. FRACTIONS

4. A. Give the fraction represented by the
shaded parts/region.
𝟒
𝟓
𝟑
𝟖
𝟏
𝟑
𝟒
𝟔
or
𝟐
𝟑
𝟏
𝟑
𝟕

5. B. Use a circle or rectangle to illustrate each of
the following fractions.
𝟑
𝟖
𝟐
𝟑
𝟑
𝟏𝟎
𝟏𝟑
𝟔
𝟏
𝟐
𝟗
1.
2.
3.
4.
5.

6. COMPARING FRACTIONS
.

7. C. Arrange the following fractions from least to
greatest.
15
8
,
17
3
,
11
5
,
7
3
,
5
2
13
8
,
11
2
,
9
8
,
7
2
,
11
4
1.
2.
15
8
,
11
5
,
7
3
,
5
2
,
17
3
9
8
,
13
8
,
11
4
,
7
2
,
11
2

8. D. Arrange the following fractions from greatest to
least.
1.
2.
7
5
1
,
5
9
,
4
3
,
10
9
,
7
6
7
3
,
7
1
1
,
11
6
,
13
5
,
5
9
4
3
,
7
6
,
10
9
,
7
5
1
,
5
9
13
5
,
7
3
,
11
6
,
7
1
1
,
5
9

9. REDUCING TO ITS
LOWEST TERMS
.

10. E. Reduce each fractions to lowest terms.
÷
𝟐
𝟐
=
𝟏
𝟓
=
𝟐
𝟓
÷
𝟓
𝟓
=
𝟏
𝟔
÷
𝟑
𝟑
=
𝟐
𝟑
÷
𝟖
𝟖
=
𝟐
𝟓
÷
𝟗
𝟗
÷
𝟒
𝟒
=
𝟑
𝟒
÷
𝟏𝟓
𝟏𝟓
=
𝟏
𝟑
÷
𝟒
𝟒
=
𝟒
𝟕
÷
𝟕
𝟕
=
𝟒
𝟕
=
𝟓
𝟗
÷
𝟑
𝟑

11. ADDITION AND SUBTRACTION
OF FRACTIONS
.

12. F. Add or Subtract the following fractions.
5
4
+
2
3
–
10
7
1.
2.
3.
8
4
–
3
1
+
12
5
9
7
–
3
2
+
7
4
=
8+15 −7
10
=
16
10
or 1
6
10
=
12−8
24
+
5
12
=
4
24
+
5
12
=
2
12
+
5
12
=
7
12
1
6
=
21−18
27
+
4
7
=
3
27
+
4
7
1
9
=
7
63
+
4
63
=
11
63

13. F. Add or Subtract the following fractions.
4.
5.
6.
5
2
+
10
3
–
15
11
12
7
5 +
24
5
–
8
5
=
2 +15
10
−
11
15
=
17
10
-
11
15
=
51
30
-
22
30
=
29
30
=
2 +15
10
−
11
15
=
17
10
-
11
15
=
51
30
-
22
30
=
29
30



7
6
11
4
7
6
=
67
12
+
5
24
−
5
8
=
134
24
-
5
24
+
15
24
=
144
24
= 6

14. MULTIPLICATION AND DIVISION
OF FRACTIONS
.

15. 3
2
5 x
2
1
3
G. Multiply.
1.
2.
3.
=
12
55
=
4
11
2
=
21
32
5
2
x
11
6
15
6
x
11
10
3
2
1
4
3
x
8
7
8 x
24
10
4.
5.
6.
=
10
3
or 3
1
3
2
4
3
x
4
1
1 =
11
4
×
5
4
1
3
=
55
16
or 3
7
16
1
1
= 15
1
3

16. H. Give the reciprocal of each of the following
fractions.
1.
2.
3.
4.
5.
11
8
11
8
18
13
5
2
3
7
5
7
7
4
2
18
13
17
5
=
5
17
54
7
=
7
54
18
7
=
7
18

17. 5
3
10
H. Give the reciprocal of each of the following
fractions.
6.
7.
8.
9.
10.
5
53
5
23
5
27
29
4
=
4
29
43
5
=
5
43
53
5
=
5
3
4
23
5
=
5
27
4
1
7
5
3
8

18. I. Divide.
1.
2.
3.
4.
=
3
4
𝑥
2
1
=
6
4
or 1
1
2
=
7
5
𝑥
18
16
=
63
40
or 1
23
40
=
7
3
𝑥
4
15
=
28
45
=
32
5
𝑥
2
5
=
64
25
or 2
14
25

19. I. Divide.
5.
6.
7.
8.
71
32

13
12
37
21

57
55
150
125

50
25
5
2
4 
3
2
3
=
32
71
𝑥
13
12
=
104
213
=
21
37
𝑥
57
55
=
1197
2035
=
125
150
𝑥
50
25
=
5
3
𝑜𝑟 1
2
3
5
1
1
3
=
22
5
𝑥
3
11
2
1
=
6
5
𝑜𝑟 1
1
5

20. I. Perform the indicated operations.
1.
2.
3.
4.
= 2
8
20
+ 5
15
20
= 7
23
20
or 8
3
20
= 9
9
12
− 4
4
12
= 5
5
12
=
9
7
𝑥
21
4
=
27
4
𝑜𝑟 6
3
4
3
1
=
14
3
𝑥
2
5
=
28
15
𝑜𝑟 1
13
15
5
2
2 +
4
3
5
4
3
9 –
3
1
4
7
2
1 x
4
1
5
3
2
4 
2
1
2

21. I. Perform the indicated operations.
5.
6.
7.
8.
=
48
5
𝑥
8
3
=
128
5
or 25
3
5
= 4
8
12
+ 5
3
12
= 9
11
12
= 7
27
45
− 3
20
45
= 4
7
45
=
26
3
𝑥
4
11
=
104
33
𝑜𝑟 3
5
33
5
3
9 x
3
2
2
16
1
3
2
4 +
4
1
5
5
3
7 –
9
4
3
3
2
8 
4
3
2
9.
7
3
9 +
3
2
4
= 9
9
21
+ 4
14
21
= 13
23
21
or 14
2
21

22. SOLVING WORD
PROBLEMS

23. J. Answer each of the following problems:
1. 3/8 of the teachers are male. 5 /12 of the teachers teach mathematics
subject .What fraction of the teacher is female?
Answer:
Solution:
therefore, 5/8 is female
8
5
8
3
8
8



24. 2. A whale weighed 5/ 6 kilograms. After two weeks, its weight was increased
by 3/ 10 kilograms. But afterwards, it lost 1/ 5 kilograms in weight as it was sick.
What is its current weight?
Answer:
Solution:
or is the
current weight of a whale.
30
28
30
6
30
9
30
25
5
1
10
3
6
5






15
14

25. 3. Justin received ₱500.00 for Christmas. He gave 1/4 of it to a poor family, 1/5
of it to each to his two sisters. How much money remained with him?
Answer:
Solution:
₱175.00 money remained with him.
. ₱500.00 x
4
1
= ₱125.00, ₱500.00 x
5
1
= ₱100.00, ₱500.00 -₱125.00 – 2(₱100.00) = ₱375.00 -
₱200.00 = ₱175.00

26. 4. Each large cookie is 5/8 oz and each small cookie is 4/9 oz. What is the total
weight of 2 large cookies and 1 small cookie?
Answer:
Solution:
weight of 2 large cookies, weight of 1
small cookie, therefore :
or .
the total weight of two large cookies and 1 small cookie.
. 2 x
8
5
=
8
10
or
4
5
9
4
36
61
36
16
36
45
9
4
4
5




36
25
1
36
25
1

27. 5. Susan earned ₱9000.00 for the sale of some piglets. She gave 1/3 of it to the
caretaker of her pigs. How much remained with her?
Answer:
Solution:
₱9000.00 x = ₱3000.00 amount given to the caregiver.
₱9000.00 - ₱3000.00 = ₱6000.00 amount given to Susan.
3
1

28. 6. There are 75 birds in a big cage. If 1/5 are parrots, 2/5 are mayas and the
rest are doves, how many of each kind of birds are there?
7. What fraction of the letters of the word “insufficient” are the vowels? What
fraction are the consonants?
Answer:
Answer:
There are parrots, are mayas. So, 75 – 45 = 30 are
doves.
1
5
x 75 = 15
2
5
x 75 = 30
There are 5 vowels out of the 12 letter-word “insufficient”, therefore by
fraction it is . There are 7 consonants out of the 12 letter-word
“insufficient”, so by fraction it is
5
12
7
12
.

29. 8. There is a bag of sugar in the storage room. The bag contained 4/5
kilograms of sugar. The chef filled up an empty can with 3/10 kilogram of sugar
and then used 7/20 of a kilogram of sugar for a cake. How much sugar was left
in the bag?
Solution:
𝟒
𝟓
−
𝟑
𝟏𝟎
−
𝟕
𝟐𝟎
=
𝟏𝟔
𝟐𝟎
−
𝟔
𝟐𝟎
−
𝟕
𝟐𝟎
=
𝟑
𝟐𝟎
𝒌𝒈. of sugar was left in the bag.
Answer:

30. 9. Zoie has ₱250. Jean has times as much as Zoie. How much money does
each girl have?
Answer:
Zoie has ₱250.00 . Jean has
𝟑
𝟐
𝟐𝟓𝟎 = 375. Jane has ₱375.00
1
1
2

31. 10. The goldfish are fed three times a day. During the morning feeding, 2/15 of
a ton of goldfish is fed. During the afternoon feeding, the weight of the goldfish
fed will be 1/15 of a ton more than the goldfish fed during the morning. If the
total weight of goldfish fed in a day is 1/2 of a ton, how much is fed during the
feeding at night?
Solution:
𝟐
𝟏𝟓
+
𝟑
𝟏𝟓
=
𝟓
𝟏𝟓
,
𝟏
𝟐
−
𝟓
𝟏𝟓
=
𝟏𝟓
𝟑𝟎
−
𝟏𝟎
𝟑𝟎
=
𝟓
𝟑𝟎
𝒐𝒓
𝟏
𝟔
were fed during at night.
Answer:

32. 11. The panda nursery is open two times a day: 2/ 3 hour at noon and 5 /12
hour in the afternoon. How much time is the penguin nursery open every day?
Solution :
𝟐
𝟑
hour +
𝟓
𝟏𝟐
=
𝟖
𝟏𝟐
+
𝟓
𝟏𝟐
=
𝟏𝟑
𝟏𝟐
or 𝟏
𝟏
𝟏𝟐
hour the nursery opens every
day.
Answer:

33. 12. John Eric spent 5/6 of an hour running and 7/8 of an hour walking.
Afterwards, he played basketball for 3/10 of an hour. How much time did John
Eric exercise before he spent playing basketball?
Solution:
𝟓
𝟔
+
𝟕
𝟖
=
𝟐𝟎
𝟐𝟒
+
𝟐𝟏
𝟐𝟒
=
𝟒𝟐
𝟐𝟒
𝐨𝐫
𝟕
𝟒
𝒐𝒓 𝟏
𝟑
𝟒
hour did John eric exercise
before he spent playing basketball.
Answer:

34. 13. Jhamia decided to walk for 6/7 mile every day to keep her fit. She walked
3/7 mile to work and walked 1/4 mile at lunchtime. How much more does she
need to walk after dinner if she wants to meet her target distance?
Solution:
𝟑
𝟕
+
𝟏
𝟒
=
𝟏𝟐
𝟐𝟖
+
𝟕
𝟐𝟖
=
𝟏𝟗
𝟐𝟖
.
𝟔
𝟕
−
𝟏𝟗
𝟐𝟖
=
𝟐𝟒
𝟐𝟖
−
𝟏𝟗
𝟐𝟖
=
𝟓
𝟐𝟖
mi., she needs to
walk after dinner if she wants to meet her target distance.
Answer:

35. 14. I am thinking of a number. 2 1/3 times my number is 210. What is my
number?
If the number is x , then
𝟕𝒙
𝟑
= 𝟐𝟏𝟎, 𝟕𝒙 = 𝟔𝟑𝟎 , 𝒙 = 𝟗𝟎.
The number is 90 .
Answer:

36. CHALLENGE!

37. Let us apply what we
learned!

38. Solve the following problems.
1. Sean has 360 chocolates. She gave 1/5 of them to his
family; 1/4 of them to his friends, 1/3 to their neighbors and the
rest to his cousins. How many chocolates were given to each
group?
Sean gave
1
5
of 360 = 72 chocolates to his family;
1
4
of 360 = 90 chocolates
to his friends,
1
4
of 360 = 120 to neighbors and 360 – (72 + 90 + 120) = 360 -282 = 78
chocolates to his cousins.

39. 2. The average of three numbers is 44. The first is 6 less
than the average, the second is 5 less than the average and
the third is 11 more than the average. What are the three
numbers?
Average of 3 numbers = 44. 1st number = 44 – 6 = 38, the second number 44 – 5 = 39
and the third number = 44 + 11 = 55.

40. 3. A big rectangle has 9 rows of smaller rectangle with 9 squares
in each row. One third of the rectangles are colored red, one
ninth is colored green, 2/3 of the remainder are blue, and the rest
are yellow. How many small rectangles are red? Green? Blue?
And Yellow
There are 9 x 9 = 81 small rectangles.
1
3
of 81 = 27 are red,
1
9
of 81 = 9 of
them are green. Of the remaining 81 – ( 27 + 9) = 45,
2
3
of 45 = 30 are blue
and the remaining 15 are yellow.

41. 4. The ones digit of a two-digit number is half of the tens digit
and their sum is 12. If the digits are interchanged the resulting
number is 36 less than the original number. Find the number.
Let a = tens digit and b = the ones digit. Since b= ½ of a, then a + ½ a = 12 , 3a = 24
therefore a= 8 and b = ½ of 8 = 4. 84 – 48 = 36 . The number is 84.

42. 5. Find a 4-digit number in which the second digit is half the first;
the third digit is the sum of the first two digits and the fourth digit
is the product of the first two digits. Can you find more than one
number?
Two possible answers are: 2132 and 4268.