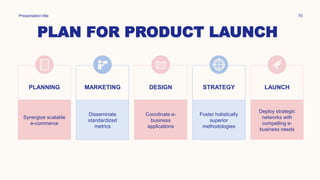
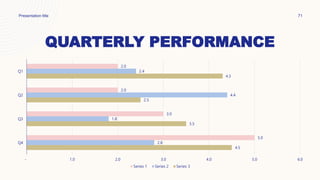
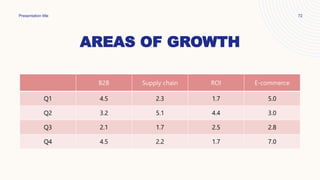
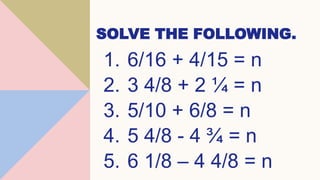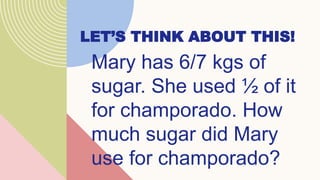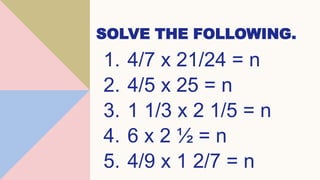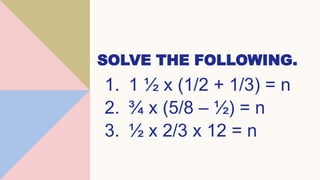This document provides lessons on dividing fractions. It begins with the learning competencies and standards for dividing simple fractions and mixed fractions. Examples are provided to demonstrate how to divide fractions by other fractions or whole numbers. The steps are to get the reciprocal of the divisor, apply cancellation if possible, then multiply the numerators and denominators. Mixed numbers should first be converted to improper fractions before dividing. Multiple choice questions assess understanding of dividing fractions. The assignment involves dividing the total amount of wax Mang Ambo has into portions for making candles.

1. MULTIPLICATION
AND DIVISION OF
FRACTIONS
GRADE 6
NOVEMBER 14-18, 2022

2. MULTIPLICATION
OF FRACTIONS
Grade 6
November 14, 2022

3. A. CONTENT STANDARDS
The learner demonstrates
understanding of the four fundamental
operations involving fractions and
decimals.

4. B. PERFORMANCE STANDARDS
The learner is able to apply the four
fundamental operations involving
fractions and decimals in mathematical
problems and real-life situations.

5. C. LEARNING COMPETENCIES
Multiplies simple fractions
and mixed fractions.
(M6NS- Ib-90.2)

6. SOLVE THE FOLLOWING.
1. 6/16 + 4/15 = n
2. 3 4/8 + 2 ¼ = n
3. 5/10 + 6/8 = n
4. 5 4/8 - 4 ¾ = n
5. 6 1/8 – 4 4/8 = n

7. LET’S DO THIS!
What is ½ of a whole?
Show it through a piece of
paper.
If you fold ½ of that part again,
what answer will you get?
Fold the paper once more in half
and shade that part.
How is the result compared to

8. LET’S THINK ABOUT THIS!
Mary has 6/7 kgs of
sugar. She used ½ of it
for champorado. How
much sugar did Mary
use for champorado?

9. LET’S DO SOME MORE!
If the given are mixed
fraction, convert mixed
fraction to improper
fraction before multiplying.
4 ½ x ¾ = n

10. ONE MORE TIME!
If the given are whole
number, convert to fraction by
making the whole number
numerator, and 1 as
denominator before
multiplying.

11. SOLVE THE FOLLOWING.
EXPRESS YOUR ANSWERS IN
LOWEST TERM.
1. ½ x 3 = n
2. 1/3 x 2/3 = n
3. 1/6 x 6 = n
4. 3/8 x ½ = n
5. 3 3/8 x 2 2/5 = n

12. WE CAN DO IT!
Discuss how the problem will be solved.
1. There are 50 pupils in a class. Four-
fifths of the class are boys. How
many are boys?
2. A coin weighs about 6 ¾ grams.
How many grams will eight of this coin
weigh?

13. WHAT I HAVE LEARNED…
How do you multiply fraction by another fraction?
How do you multiply fraction by a whole
number?
How do you multiply fraction by a mixed
fraction?

14. CHOOSE THE LETTER OF THE CORRECT ANSWER.
1. HOW DO WE MULTIPLY FRACTIONS?
a. Change dissimilar fractions to similar fractions then multiply the
numerators and denominators.
b. Apply cancellation, if possible, then multiply the numerators and
denominators, check if the answer is expressed in lowest term.
c. Get the reciprocal of the second fraction before multiplying the
numerators and the denominators.
d. Apply butterfly method to get the answer in lowest term.

15. 2. WHAT DO WE DO IF THE GIVEN IS A MIXED FRACTION?
a. Convert to similar fractions.
b. Convert to lowest terms.
c. Convert to dissimilar fractions.
d. Convert to improper fraction.
3. DETERMINE THE VALUE OF N IN THE EQUATION:
1 2/15 X 20 = N
a. 28 2/3 c. 32 2/3
b. 38 2/3 d. 22 2/3

16. 4. ONE CRATE OF MANGOES WEIGHS 14 1/2 KG. THERE
ARE TWENTY-FOUR CRATES IN ALL. WHAT IS THE TOTAL
WEIGHT OF MANGOES?
a. 264 kilos c. 400 kilos
b. 348 kilos d. 528 kilos
5. LITO TRIES TO LIFT THE TRUNK OF A TREE WHICH
WEIGHS TWICE AS HIM. IF HE WEIGHS 31 ½ KG, HOW
HEAVY IS THE TRUNK?
a. 63 kg c. 64 kg
b. 52 kg d. 51 kg

17. CORRECT ANSWERS:
17
1. B
2. D
3. D
4. B
5. A

18. ASSIGNMENT:
In a local supermarket,
3/5 kilogram of squid
costs P156.00. How
much do 4 kilograms of
squid cost?

19. SOLVING WORD
PROBLEM
INVOLVING
MULTIPLICATION
OF FRACTIONS
Grade 6
November 15, 2022

20. A. CONTENT STANDARDS
The learner demonstrates
understanding of the four fundamental
operations involving fractions and
decimals.

21. B. PERFORMANCE STANDARDS
The learner is able to apply the four
fundamental operations involving
fractions and decimals in mathematical
problems and real-life situations.

22. C. LEARNING COMPETENCIES
Solves routine or non-routine problems
involving multiplication without or with
addition or subtraction of fractions and
mixed fractions using appropriate
problem-solving strategies and tools.
(M6NS-Ib-92.2)

23. SOLVE THE FOLLOWING.
1. 4/7 x 21/24 = n
2. 4/5 x 25 = n
3. 1 1/3 x 2 1/5 = n
4. 6 x 2 ½ = n
5. 4/9 x 1 2/7 = n

24. LET’S DO THIS!
Do you save money?
Why?
Why not?
Is saving money
important to the

25. LET’S THINK ABOUT THIS!
Mr. Revilla earns P48, 150.00
every month. He saves 2/9 of it
and spends the remaining amount
of money on food and rent. How
much does he spend on food and
rent every month? How much
money will he save after a year?

26. LET’S DO SOME MORE!
Use the 4-step plan to solve the
problem.
1. A vacant lot near your residence is
for sale. The lot is in rectangular form
having a length of 3 3/9 units and
width of 5 3/6 units. The piece of lot
per square unit is P100.00. What is
the total value of the lot?

27. ONE MORE TIME!
Let the class solve the problem. Ask a
volunteer to discuss their answer.
Alexa takes ¼ hour to ride her bicycle to
find her friend’s house. If Alexa walks
instead, the trip takes her 2 ½ times long.
How long does Alexa take to walk to her
friend’s house?
A. in hours

28. WE CAN DO IT!
Discuss how the problem will be solved.
1. There are 50 pupils in a class. Four-
fifths of the class are boys. How
many are boys?
2. A coin weighs about 6 ¾ grams.
How many grams will eight of this coin
weigh?

29. WHAT I HAVE LEARNED…
How do we solve word problem?
Enumerate the steps.
Why do we have to check our answers
after solving the equation?

30. CHOOSE THE LETTER OF THE CORRECT ANSWER.
1. WHAT IS THE CORRECT ARRANGEMENT OF THE
STEPS IN PROBLEM SOLVING?
a. What is asked?, What are the given?, What operation/s to be
used?,
Write your equation, Show your solution, and check your final answer.
b. What operation/s to be used?, What is asked?, What are the
given?, Write your equation, Show your solution.
c. Write your equation, Show your solution, and check your final
answer.
d. What is asked?, What are the given?, Show your solution, and
check your final answer.

31. 2. DURING YEAR-END SALE, THE COST OF A TV SET IS ₱ 18,355.35.
ITS PRICE HAS BEEN REDUCED BY 2/10 OF THE ORIGINAL PRICE.
WHAT WAS THE PRICE OF THE TV SET BEFORE THE SALE?
WHAT IS ASKED IN THE PROBLEM?
3. MARY COUNTED 160 FAMILIES IN A BARANGAY. SHE FOUND OUT
THAT 40 FAMILIES WERE ENGAGED IN VEGETABLE GARDENING. IT
MEANS ¼ OF THEM ARE FARMERS. WHAT DID SHE DO TO GET SUCH
CONCLUSION?
a. The original cost of the TV set.
b. The discounted price of the TV set.
c. The amount of discount during the sale.
d. The duration of the year-end sale.
a. addition
b. subtraction
c. multiplication
d. simplifying fraction

32. 4. A KILO OF RICE COSTS ₱45.00. HOW MUCH WILL
2 ¾ KILOS OF RICE COST?
WHAT IS THE EQUATION IN THE PROBLEM?
a. 45 ¾ x 2 = n c. 45x 2 ¾
= n
b. 45/4 x 3 = n d. ¾ x 45
= n
5. MARK CAN PAINT 8 ½ SQUARE METERS PER HOUR.
AT THE SAME RATE, HOW MANY SQUARE METERS CAN
HE PAINT IN 2 ½ HOURS?
WHAT IS THE CORRECT EQUATION IN THE PROBLEM?
a. 8 ½ x 2 ½ = 21 c. 8 ½ x 2 ½ = 16 ¼
b. 8 ½ x 2 ½ = 17 d. 8 ½ x 2 ½ =15

33. CORRECT ANSWERS:
33
1. A
2. B
3. D
4. C
5. A

34. ASSIGNMENT:
A square lot, which is 6 3/5
m on each side, is covered
with Bermuda grass. The lot
is surrounded by a cemented
path 1 ¼ m wide. Find the
area of the cemented path.

35. DIVISION OF
FRACTIONS
Grade 6
November 16, 2022

36. A. CONTENT STANDARDS
The learner demonstrates
understanding of the four fundamental
operations involving fractions and
decimals.

37. B. PERFORMANCE STANDARDS
The learner is able to apply the four
fundamental operations involving
fractions and decimals in mathematical
problems and real-life situations.

38. C. LEARNING COMPETENCIES
Divides simple fractions and
mixed fractions.
(M6NS- Ic-96.2)

39. SOLVE THE FOLLOWING.
1. 1 ½ x (1/2 + 1/3) = n
2. ¾ x (5/8 – ½) = n
3. ½ x 2/3 x 12 = n

40. LET’S DO THIS!
Complete the following statement about
multiplication and division of fractions.
1. To multiply fractions,
_________________________.
2. To multiply mixed numbers,
_______________.
3. Final answers in operations with
fractions must always be expressed in
_____________.

41. LET’S THINK ABOUT THIS!
Emma bought 1/2 cake for
a party. Each child at the
party received 1/6 of a
cake. How many children
did Emma give the cakes
to?

42. LET’S DO SOME MORE!
If the given are mixed
fraction, convert mixed
fraction to improper
fraction before dividing.
2 ½ ÷ 1 ¼ = n

43. ONE MORE TIME!
If the given are whole
number, convert to fraction by
making the whole number
numerator, and 1 as
denominator before dividing.
18 ÷ 1 1/8 = n

44. SOLVE THE FOLLOWING.
EXPRESS YOUR ANSWERS IN
LOWEST TERM.
1. 1/3 ÷ 3 = n
2. 1 ¼ ÷ 5/15 = n
3. 3 ¾ ÷ 1 ¼ = n
4. (4/9 x3) ÷ (3/5 – 1/3)= n
5. (2 4/9 x 6/11) ÷ (5 ¾ - 1/3) =

45. WE CAN DO IT!
Discuss how the problem will be solved.
1. Mr. Cruz bought a loaf of bread for
breakfast. It measures 18 inches long.
How many slices can she make if
each slice measures 1 1/8 inches
long?
2. Each costume for a school play
requires 3 ½ yards of cloth. How many

46. WHAT I HAVE LEARNED…
How do you divide fraction by another fraction?
How do you divide fraction by a whole number?
How do you divide mixed number by a mixed
number?

47. CHOOSE THE LETTER OF THE CORRECT ANSWER.
1. HOW DO WE DIVIDE FRACTIONS?
a. Get the reciprocal of the divisor, apply cancellation, if possible,
then multiply the numerators and then the denominators, lastly, check
if the answer is expressed in lowest term.
b. Apply cancellation, if possible, then divide the numerators and
denominators, check if the answer is expressed in lowest term.
c. Apply cancellation, if possible, get the reciprocal of the divisor,
then multiply the numerators and denominators, check if the answer
is expressed in lowest term.
d. Apply butterfly method to get the answer in lowest term.

48. 2. WHAT DO WE DO IF THE GIVEN IS A MIXED FRACTION?
a. Convert to similar fractions.
b. Convert to lowest terms.
c. Convert to dissimilar fractions.
d. Convert to improper fraction.
3. DETERMINE THE VALUE OF N IN THE EQUATION:
4 3/8 ÷ 2 1/3 = N
a. 15/8 c. 1 4/8
b. 1 7/8 d. 1 3/8

49. 4. JOANA IS MAKING CAKES FOR A PARTY. SHE USES ¼
CUP OF OIL FOR EACH CAKE. HOW MANY CAKES CAN
SHE MAKE IF SHE HAS 8 CUPS OF OIL?
a. 24 c. 32
b. 30 d. 36
5. MARTHA HAS 5 1/2 M OF CLOTH. SHE NEEDS 1 ¼
METER OF CLOTH TO MAKE ONE PROP. HOW MANY
PROPS CAN SHE MAKE OUT OF THE CLOTH?
a. 4 ¼ c. 4
b. 4 2/5 d. 5

50. CORRECT ANSWERS:
50
1. A
2. D
3. B
4. C
5. B

51. ASSIGNMENT:
Mang Ambo makes decorative
candles to sell on ‘All Souls Day’.
He has 15 ½ kg of wax. He
bought 20 ¼ kg more. If he uses
1 3/5 kg each candle, how many
candles can he make?

52. SOLVING WORD
PROBLEM
INVOLVING
DIVISION OF
FRACTIONS
Grade 6
November 17, 2022

53. A. CONTENT STANDARDS
The learner demonstrates
understanding of the four fundamental
operations involving fractions and
decimals.

54. B. PERFORMANCE STANDARDS
The learner is able to apply the four
fundamental operations involving
fractions and decimals in mathematical
problems and real-life situations.

55. C. LEARNING COMPETENCIES
Solves routine or non-routine problems
involving division without or with any of
the other operations of fractions and
mixed fractions using appropriate
problem-solving strategies and tools.
(M6NS-Ic-97.2)

56. SOLVE THE FOLLOWING.
1. 3 1/5 ÷ 1 5/7 = n
2. (2/3 ÷ 1/3) ÷ ¼ = n
3. 2 8/9 ÷ (1/2 ÷ 2/3) = n
4. 5/6 ÷ (2 ½ ÷ ½)= n
5. (5/6 ÷ 4 3/10) ÷ 3/5 =

57. LET’S DO THIS!
Complete the following statement about multiplication
and division of fractions.
1. To multiply fractions,
_________________________.
2. To multiply mixed numbers, _______________.
3. To divide fractions, _________________________.
4. To divide mixed numbers, _______________.
5. Final answers in operations with fractions must

58. LET’S THINK ABOUT THIS!
An 8/10 m of wood is cut
equally into shorter
pieces of 1/5 m of each.
How many shorter pieces
will be there?

59. LET’S DO SOME MORE!
Use the 4-step plan to solve the
problem.
1. The barangay chairman plans to
have flower pots along their 4 3/5
km road. If the pots must be 1/10
km apart, how many flower pots
must be used on one side of the

60. WE CAN DO IT!
Discuss how the problem will be solved.
1. Francis is a working student at a fast-food
restaurant. This week, he worked 4/8 as
many hours as he did last week. He worked
10 hours last week. How many hours did he
work this week?

61. WHAT I HAVE LEARNED…
How do we solve word problem?
Enumerate the steps.
Why do we have to check our answers
after solving the equation?

62. CHOOSE THE LETTER OF THE CORRECT ANSWER.
1. WHAT IS THE CORRECT ARRANGEMENT OF THE
STEPS IN PROBLEM SOLVING?
a. What is asked?, What are the given?, What operation/s to be
used?,
Write your equation, Show your solution, and check your final answer.
b. What operation/s to be used?, What is asked?, What are the
given?, Write your equation, Show your solution.
c. Write your equation, Show your solution, and check your final
answer.
d. What is asked?, What are the given?, Show your solution, and
check your final answer.

63. 2. A BAMBOO IS 26 2/5 METERS LONG. IF IT IS CUT
INTO 12 PIECES, HOW LONG WILL EACH PIECE BE?
WHAT IS ASKED IN THE PROBLEM?
3. IN DIVIDING FRACTIONS, WE MUST FIRST GET THE
RECIPROCAL OF THE DIVISOR BEFORE APPLYING THE RULES IN
MULTIPLICATION OF FRACTIONS. HOW CAN WE GET THE
RECIPROCAL OF A MIXED FRACTION?
a. The length of the bamboo.
b. How many pieces the bamboo will be cut into.
c. Who will cut the bamboo.
d. The length of each piece of the bamboo after it is divided into 12 equal parts.
a. Flip the numerator and denominator first, and then convert to improper fraction.
b. Convert the mixed fraction to improper fraction and flip the numerator and denominator.
c. Set aside the whole number and flip the numerator and denominator.
d. Reciprocal is not needed if the divisor is mixed fraction.

64. 4. MYRNA HAS A 12 ¾ M LONG CLOTH. HOW MANY
BLOUSES CAN SHE MAKE IF EACH BLOUSE USES A
1 ½ M OF CLOTH?
WHAT IS THE EQUATION IN THE PROBLEM?
a. 1 ½ ÷ 12 ¾ = n c. 12 ¾ ÷ 1 ½ = n
b. ¾ ÷ ½ = n d. 12 ÷ 1 = n
5. A FLOATING RESTAURANT CONTAINS 105
OCCUPIED SEATS AND IT WAS 7/9 FILLED. HOW MANY
EMPTY SEATS ARE THERE?
WHAT IS THE CORRECT EQUATION IN THE PROBLEM?
a. 105 ÷ 7/9 = 30 c. (7/9 ÷ 105) –
105 = 30
b. 135 – 105 = 30 d. (105 ÷ 7/9) –

65. CORRECT ANSWERS:
Multiplication of Fractions 65
1. A
2. D
3. B
4. C
5. D

66. ASSIGNMENT:
Multiplication of Fractions
A square lot, which is 6 3/5
m on each side, is covered
with Bermuda grass. The lot
is surrounded by a cemented
path 1 ¼ m wide. Find the
area of the cemented path.

67. QUESTION
BANK
5. SAM CAN ANSWER A DOZEN OF MATH PROBLEMS
IN ¾ HOUR. HOW MANY PROBLEMS CAN HE ANSWER
IN 4 ¼ HOURS?
WHAT IS THE CORRECT EQUATION IN THE PROBLEM?
a. (12 x ¾) x 4 ¼= 68

68. MEET OUR TEAM
Presentation title 68
TAKUMA HAYASHI
President
MIRJAM NILSSON
Chief Executive Officer
FLORA BERGGREN​
Chief Operations Officer
RAJESH SANTOSHI​
VP Marketing

69. MEET OUR EXTENDED TEAM
TAKUMA HAYASHI
President
GRAHAM BARNES
VP Product
MIRJAM NILSSON
Chief Executive Officer
ROWAN MURPHY
SEO Strategist
FLORA BERGGREN​
Chief Operations Officer
ELIZABETH MOORE
Product Designer
RAJESH SANTOSHI​
VP Marketing
ROBIN KLINE
Content Developer
69

70. PLAN FOR PRODUCT LAUNCH
Presentation title 70
PLANNING
Synergize scalable
e-commerce
MARKETING
Disseminate
standardized
metrics
DESIGN
Coordinate e-
business
applications
STRATEGY
Foster holistically
superior
methodologies
LAUNCH
Deploy strategic
networks with
compelling e-
business needs

71. QUARTERLY PERFORMANCE
4.5
3.5
2.5
4.3
2.8
1.8
4.4
2.4
5.0
3.0
2.0
2.0
- 1.0 2.0 3.0 4.0 5.0 6.0
Q4
Q3
Q2
Q1
Series 1 Series 2 Series 3
Presentation title 71

72. AREAS OF GROWTH
Q1 4.5 2.3 1.7 5.0
Q2 3.2 5.1 4.4 3.0
Q3 2.1 1.7 2.5 2.8
Q4 4.5 2.2 1.7 7.0
Presentation title 72