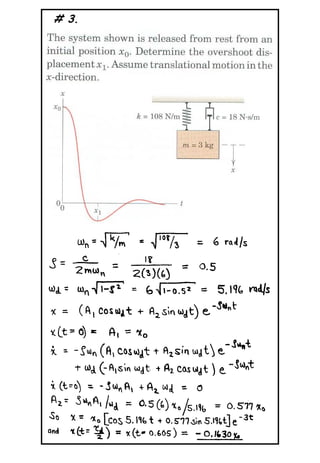
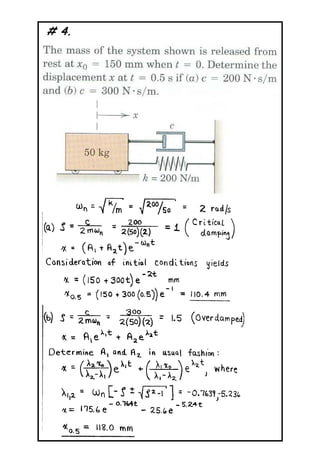
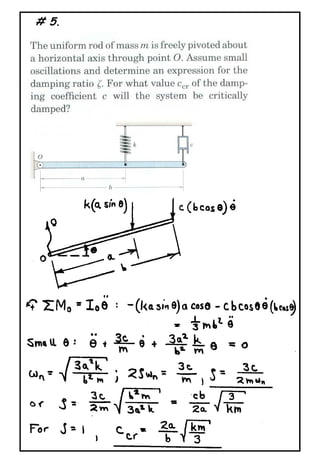
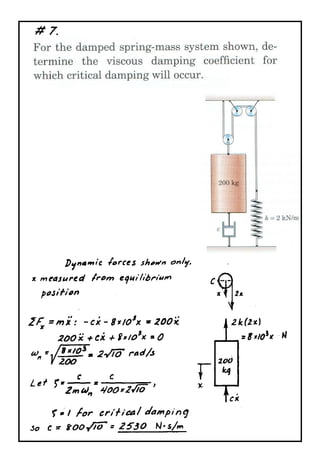
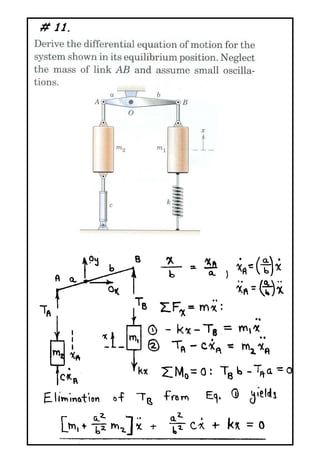
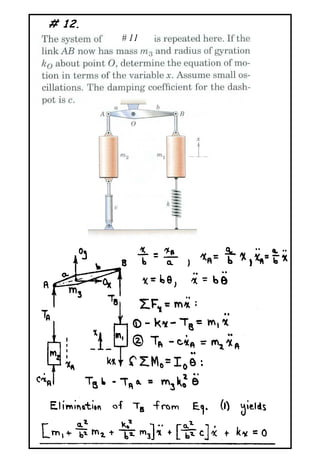
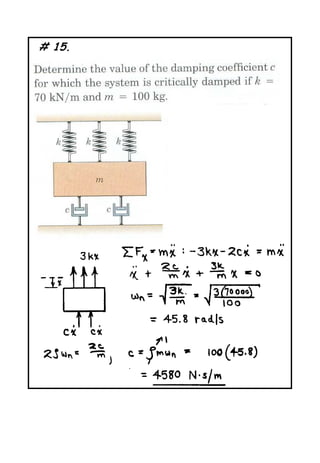
The document describes a problem involving a damped spring-mass system. It is determined that the system is underdamped with a damping ratio of 0.625. The damped natural frequency is calculated to be 1.561 rad/s. The displacement of the mass at time t=2s is calculated to be -0.01616m.

1. 610 Chapter 8 Vibration and Time Response
Sample Problem 8/2
The 8-kg body is moved 0.2 m to the right of the equilibrium position and
released from rest at time t 0. Determine its displacement at time t 2 s. The
viscous damping coefficient c is 20 N s/m,
and the spring stiffness k is 32 N/m.
Solution. We must first determine whether the system is underdamped, criti-cally
damped, or overdamped. For that purpose, we compute the damping ratio .
n k/m 32/8 2 rad/s c
2mn
20
2(8)(2)
0.625
Since 1, the system is underdamped. The damped natural frequency is
1 2 21 (0.625)2
dn 1.561 rad/s. The motion is given by Eq. 8/12
and is
x Cent sin (dt ) Ce1.25t sin (1.561t )
The velocity is then
x˙ 1.25Ce1.25t sin (1.561t ) 1.561Ce1.25t cos (1.561t )
Evaluating the displacement and velocity at time t 0 gives
x0 C sin 0.2 x˙0 1.25C sin 1.561C cos 0
Solving the two equations for C and yields C 0.256 m and 0.896 rad.
Therefore, the displacement in meters is
x 0.256e1.25t sin (1.561t 0.896)
Evaluation for time t 2 s gives x20.01616 m. Ans.
k
x
c
8 kg
x
Equilibrium
position
mg
N
·
cx ·
= 20x kx = 32x
Helpful Hint
We note that the exponential factor
e1.25t is 0.0821 at t 2 s. Thus,
0.625 represents severe damp-ing,
although the motion is still
oscillatory.

2. Sample Problem 8/8
The uniform bar of mass m and length l is pivoted at its center. The spring
of constant k at the left end is attached to a stationary surface, but the right-end
spring, also of constant k, is attached to a support which undergoes a harmonic
motion given by yB b sin t. Determine the driving frequency c which causes
resonance.
Solution. We use the moment equation of motion about the fixed point O to
obtain
k l
2
sin l
2
cos kl
2
sin yB l
Assuming small deflections and simplifying give us
¨ 6k
m
6kb
ml
2
sin t
cos 1
12
ml2 ¨
The natural frequency should be recognized from the now-familiar form of the
equation to be
6k/m
n 6k/m
Thus, c n will result in resonance (as well as violation of our small-angle
assumption!). Ans.
yB O
= b sin ωt
B
m
k
l—2
l—2
k
Helpful Hints
As previously, we consider only the
changes in the forces due to a move-ment
away from the equilibrium
Oy
mg
Ox
θ
2
k ( sin θ
) l—k 2
l—( sin θ
– y) Bposition.
¨ 2
The standard form here is
where M0 and IO
The natural frequency n of a
system does not depend on the exter-nal
disturbance.
1
12
ml2.
klb
2
M0 sin t
IO
,
n

3. Sample Problem 8/9
Derive the equation of motion for the homogeneous circular cylinder, which
rolls without slipping. If the cylinder mass is 50 kg, the cylinder radius 0.5 m,
the spring constant 75 N/m, and the damping coefficient 10 determine
(a) the undamped natural frequency
(b) the damping ratio
(c) the damped natural frequency
(d) the period of the damped system.
In addition, determine x as a function of time if the cylinder is released from rest
at the position x0.2 m when t 0.
Solution. We have a choice of motion variables in that either x or the angular
displacement of the cylinder may be used. Since the problem statement in-volves
x, we draw the free-body diagram for an arbitrary, positive value of x and
write the two motion equations for the cylinder as
[ΣFx m¨x] c˙x kx F m¨x
¨x r ¨.
The condition of rolling with no slip is Substitution of this condition
into the moment equation gives F Inserting this expression for the
friction force into the force equation for the x-direction yields
12
Comparing the above equation with that for the standard damped
oscillator, Eq. 8/9, allows us to state directly
(a) Ans.
2n 2
c
m
1
c
mn
10
3(50)(1)
(b) Ans.
3
3
0.0667
Hence, the damped natural frequency and the damped period are
(c) d n1 2 (1)1 (0.0667)2 0.998 rad/s
Ans.
(d) Ans.
d 2/d 2/0.998 6.30 s
From Eq. 8/12, the underdamped solution to the equation of motion is
x Cent sin (dt ) Ce(0.0667)(1)t sin (0.998t )
The velocity is ˙x 0.0667Ce0.0667t sin (0.998t )
x˙
0.998Ce0.0667t cos (0.998t )
At time t 0, x and become
x0 C sin 0.2
x˙0 0.0667C sin 0.998C cos 0
The solution to the two equations in C and gives
C 0.200 m 1.504 rad
Thus, the motion is given by
x 0.200e0.0667t sin (0.998t 1.504) m Ans.
n
2 2
3
k
m
cx˙ kx 1
2
mx¨ mx¨ or x¨ 2
3
c
m
x˙ 2
3
k
m
x 0
mx¨.
Fr 12
[ΣMG I ¨] mr2 ¨
N s/m,
Article 8/4 Vibration of Rigid Bodies 637
x
m
k r c
Helpful Hints
The angle is taken positive clock-wise
to be kinematically consistent
The friction force F may be as-sumed
in either direction. We will
find that the actual direction is to
the right for x 0 and to the left
for x 0; F 0 when x 0.
F
mg
O
N
with x.
Equilibrium
position
x
+θ
kx cx·
n 2
3
k
m 2
3
75
50 1 rad/s

4. # 1.

5. # 2.

6. # 3.

7. # 4.

8. # 5.

9. # 6.

10. # 7.

11. # 8.

12. # 9.

13. # 10.

14. # 11.

15. # 11
# 12.

16. # 13.

17. # 14.

18. # 15.

19. # 16.