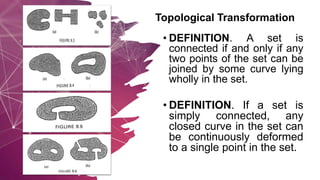
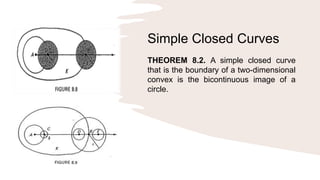
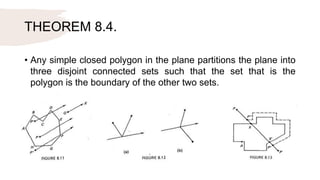
The document discusses several theorems in topological transformation and simple closed curves. It defines topological transformation as the study of properties of a set of points invariant under continuous transformations. It also examines theorems like the Jordan Curve Theorem, which states that a simple closed curve partitions the plane into an interior and exterior region.

1. Geometric Topology
8.1. TOPOLOGICAL TRANSFORMATION
8.2. SIMPLE CLOSED CURVE

2. Topological Transformation
• Topology is sometimes called “Rubber Sheet”
Geometry.
• It can be seen that the image of a circle could be an
ellipse, a triangle, or a polygon. For example, straight
lines are not necessarily changed into straight lines.
• A topology on a set X is a collection of subsets of X, called open
sets, that satisfy certain axioms.

3. Topological Transformation
• Topology is one of the modern geometries created
within the past and outstanding names of history
which include A.F. Moebius (1790-1868), J.B. Listing
(1808-1882) and Bernhard Riemann (1826-1866)
• The study of topology continues to grow and develop
with some American mathematicians.

4. Topological Transformation
• DEFINITION. Topology is the study of those properties
of a set of points invariant under the group of
bicontinuous transformations of a space onto itself.
• DEFINITION. A transformation ʄ is bicontinuous if and
only if ʄ and ʄ-1 are both continuous.

5. Doughnut-
shaped or Torus

6. Topological Transformation
• The concept of a continuous
transformation, used extensively in
calculus, since its definition makes
use of the topological concept of
neighborhood of a point.
THEOREM 8.1 The set of topological
transformations of a space onto itself is
group of transformations.

7. Question to Theorem 8.1
• Explain why the inverse of a bicontinuous transformation is
always a bicontinuous transformation.
 A bicontinuous transformation is a function that is both
continuous and has a continuous inverse. If we have a bicontinuous
transformation, it preserves the topological properties of the space
acting on it specifically, it maps open sets to open sets, closed sets
to closed sets, and preserves the notion of connectedness and
compactness.

8. Question to Theorem 8.1
• Explain why the inverse of a bicontinuous transformation is
always a bicontinuous transformation.
 Considering the inverse of a bicontinuous transformation and its
inverse. Since the original transformation is continuous and bijective
(one-to-one and onto), its inverse exist and also bijective. Since the
original transformation is continuous, we know that its inverse is also
continuous.

9. Question to Theorem 8.1
• Explain why the inverse of a bicontinuous transformation is
always a bicontinuous transformation.
 In this case, the composition of the bicontinuous transformation
and its inverse, since bicontinuous transformation maps open sets to
open sets, it follows that the composition maps open sets to open
sets which is similar to the inverse of the bicontinuous transformation,
then the composition of the inverse with the original transformation
also maps open sets to open set.

10. Topological Transformation
• DEFINITION. A set is
connected if and only if any
two points of the set can be
joined by some curve lying
wholly in the set.
• DEFINITION. If a set is
simply connected, any
closed curve in the set can
be continuously deformed
to a single point in the set.

11. • DEFINITION. In general, if 𝑛 − 1 nonintersecting cuts are
needed to convert a set into simple connected set, the is n-
tuple connected.

12. Simple Closed Curves
THEOREM 8.2. A simple closed curve
that is the boundary of a two-dimensional
convex is the bicontinuous image of a
circle.

13. • Some proofs of the fundamental
theorem of algebra depend on an
application of topology using
ideas very similar to those in the
proof of Theorem 8.2.
• Consider the intuitive notion of
tracing a simple closed curve by
moving a pencil over a piece of
paper, subject only to restriction
that you cannot cross a previous
path and that you must return to
the starting point.

14. THEOREM 8.3.
JORDAN CURVE
THEOREM
• A simple closed curve in the
plane partitions the plane into
three disjoint connected sets
such that the set is the curve
is the boundary of both the
other sets.

15. THEOREM 8.4.
• Any simple closed polygon in the plane partitions the plane into
three disjoint connected sets such that the set that is the
polygon is the boundary of the other two sets.

16. THEOREM 8.5.
• For one point A in the interior and one point B in the exterior of a
simple closed curve S. AB ∩ S is not empty.
• To prove this theorem, we will use the Jordan Curve Theorem, which states that
any simple closed curve in the plane divides the plane into exactly two regions:
an interior and an exterior. Let A be a point in the interior of the simple closed
curve S, and let B be a point in the exterior of S. Assume for contradiction that the
line segment AB does not intersect S. Then, we can draw a small circle centered
at A that lies entirely inside the interior region of S. Similarly, we can draw a small
circle centered at B that lies entirely outside the exterior region of S.

17. THEOREM 8.5.
• For one point A in the interior and one point B in the exterior of a
simple closed curve S. AB ∩ S is not empty.
• Since the two circles do not intersect S, we can draw a curve that connects the two circles
and lies entirely in either the interior or exterior region of S. Without loss of generality,
assume that the curve lies in the interior region. Then, by the Jordan Curve Theorem, the
curve must intersect S at least twice, once when it enters the exterior region and once
when it re-enters the interior region. However, this contradicts the fact that the curve lies
entirely in the interior region and does not intersect S. Therefore, our assumption that the
line segment AB does not intersect S must be false, and we conclude that the line
segment must intersect S.

18. THEOREM 8.6.
• Every ray with an endpoint in the interior of a simple closed
curve intersects the curve.
• To prove this theorem, we will use the Jordan Curve Theorem, which states that any
simple closed curve in the plane divides the plane into exactly two regions: an interior and
an exterior. Let C be a simple closed curve in the plane, and let P be a point in the interior
of C. Let R be a ray with endpoint P that does not intersect C. Consider the set of all
points that can be connected to P by a line segment that does not intersect C. This set
consists of two parts: the set of points in the interior of C, and the set of points in the
exterior of C. Since P is in the interior of C, we know that the set of points in the interior of
C is nonempty.

19. THEOREM 8.6.
• Every ray with an endpoint in the interior of a simple closed
curve intersects the curve.
• Choose a point Q in the set of points in the interior of C that is closest to P. Let r be the
line segment connecting P and Q. Since Q is in the interior of C, r intersects C at some
point S. Now consider the triangle formed by P, Q, and S. Since S is on the boundary of
the interior of C, the entire triangle must lie in the interior of C. In particular, the endpoint P
of the ray R is contained in this triangle. But this implies that the ray R intersects the line
segment r at a point T, which lies on C. Therefore, the ray R intersects the curve C, as
desired.