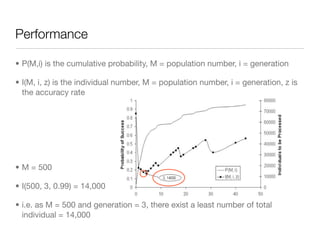
The document discusses using genetic programming with lambda abstractions and recursion to solve problems like parity. It outlines challenges with recursion in genetic programming like infinite loops. A new strategy is proposed using implicit recursion with higher-order functions like fold, lambda abstractions to define program structure, and a type system to preserve semantics. An experiment applies this approach to the even-n-parity problem, generating programs that work for any input size with high success rates using fewer individuals than other methods.

1. Genetic Programming
Recursion, Lambda Abstractions and Genetic Programming
by Tina Yu and Chris Clack
Yun-Yan Chi

2. Outline
❖Introduction ❖Experimentation
❖Background ❖fitness
❖The problem with recursion ❖crossover
❖Presentations ❖Resulting and analysis
❖The experiment ❖Experiment result
❖New strategy ❖Performance
❖Implicit recursion ❖Conclusion
❖λ abstraction
❖Type system

3. Background - Genetic Programming
• [Nichael L. Cramer - 1985]
• [John R. Koza - 1992]
• evolutionary-based search strategy
• dynamic and tree-structure representation
• favors the use of programming language that naturally embody tree structure

4. Shortcoming of GP
• simple problems suitability
• very computationally intensive
• hardware dependency

5. Enhance GP
• John R. Koza - 1994
• supporting modules in program representation
• module creation
• module reuse
• e.g. function, data structure, loop, recursive etc.
• here, we focus on the behavior of recursion

6. The problem with recursion (1/3)
• infinite loop in strict evaluation
• finite limit on recursive calls [Brave - 1996]
• finite limit on execution time [Wong & Leung - 1996]
• the “Map” function [Clack & Yu - 1997]
• “Map”, a higher-order function, can work on a finite list
• a non-terminated program with good properties
may or may not be discarded in selection step

7. The problem with recursion (2/3)
• infinite loop in lazy evaluation
• all the pervious methods are suitable in this evaluating strategy
• “map” can also work on a infinite list in lazy evaluation very well
• with lazy strategy, we can keep some potential solutions
that contain infinite loop

8. The problem with recursion (3/3)
• without semantics measuring
• GP uses a syntactic approach to construct programs
• will not consider any semantical conditions
• here, using type system to describe semantics, very lightly

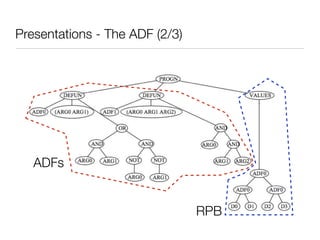
9. Presentations - The ADF (1/3)
• Automatically Defined Function (ADF) [Koza - 1994]
• Divide and Conquer:
• each program in population contains two main parts:
i. result-producing branch (RPB)
ii.definition of one or more functions (ADFs)

10. Presentations - The ADF (2/3)
ADFs
RPB

11. Presentations - The ADF (3/3)
• there are two kind of module creating in ADFs
i. statically, define ADFs before running GP
- have no opportunity to explore more advantageous structure
ii.randomly, define ADFs during the 1st generation
- crazy computationally expensive
• using GP with ADF is more powerful approach than using GP alone

12. Presentations - The λ abstraction
• λ abstraction is a kind of anonymous
• λ abstraction can to do everything what ADF can
• it can be easy to reuse by supporting with higher-order function
what could take function as argument
• by the using of higher-order function, we can adopt a middle ground:
dynamically module specify

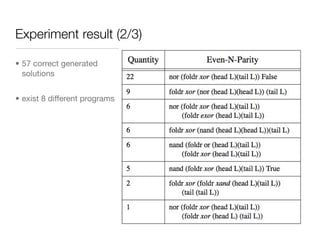
13. The experiment (1/2)
• Even-N-Parity problem
• has been used as a difficult problem for GP [Koza - 1992]
• returning True if an even number of input are true
• Function Set {AND, OR, NAND, NOR}
• Terminal Set {b0, b1, ..., bN-1} with N boolean variables
• testing instance consists of all the binary strings with length N
[00110100] → 3 → False
[01100101] → 4 → True

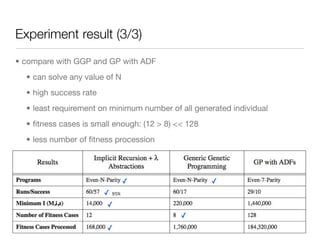
14. The experiment (2/2)
• using GP only [Koza - 1992]
• can solve the problem with very high accuracy when 1 ≤ N ≤ 5
• using GP with ADF [Koza - 1994]
• can solve this problem up to N = 11
• using GP with a logic grammar [Wong & Leung - 1996]
• according to the Curry-Howard Isomorphism, a logic system consists a
type system that can describe some semantics
• strong enough to handle any value of N
• however, any noisy case will increase the computational cost

15. New strategy
• there are three key concepts
i. implicit recursion
- to generate general solutions that work for any value of N
ii.λ abstraction (higher-order function)
- to present the module mechanism
iii.type system
- to preserve the structure (semantics) of program

16. Implicit recursion (1/2)
• this term, “implicit recursion”, states a kind of function that define the
structure of recursion
• i.e. implicit recursion is a higher-order function that takes another function as
the behavior of recursion, i.e. semantics
• usually, implicit recursions are also polymorphic
• there are several higher-order functions: fold, map, filter, etc...
• in fact, all of those functions can be defined by fold
• thus, we take foldr, a specific fold, to specify recursive structure of program

17. Implicit recursion (2/2)
• fold have two major advantages
I. with implicit recursion, the program do not produce infinite loop
- can use the pre-defined recursive structure only
II. fold is very suitable because fold takes a list as input and return a single
value
- functor is just a structural definition without any semantics

18. λ abstraction
• we use λ function as what the program will do actually
• i.e. the parameter of fold, this means that fold reuse the defined λ function
• using de Burjin denotation to make parameter number explicit
• de Burjin index : denote the outmost parameter with smallest index
β
• λ0. λ1. (+ P0 P1) 10 = λ1. (+ 10 P1)

19. Type system (1/4)
• using type system to reserve the structure of program
• for example: in even-n-parity, program :: [Bool] → Bool
• we can also using type system to run GP with slight semantics
• perform type checking during crossover and mutation
• to ensure the resulting program is reasonable

20. Type system (2/4)
• simple second-order polymorphic type system

21. Type system (3/4)
• type inferring rule:
I. constants
II.variables
III.application
IV.function

22. Type system (4/4)
• foldr :: (a→b→b) →b →[a] →b
• glue function (induction) (a→b→b) →b →[a] →b
• base case (a→b→b) →b →[a] →b
• foldr takes two arguments and return a function
that takes a list of some type a and return a single value with type b
• example: foldr (+) 0 [1,2,3] = foldr (+) 0 (1:(2:(3:[ ]))) = (1+(2+(3+0))) = 6
• another example: foldr xor F [T,F] = (xor T (xor F F)) = (xor T F) = T
• another example: foldr (λ.λ.and T P1) T [1,2] = ((λ.λ.and T P1) 1 ((λ.λ.and T P1)
2 ((λ.λ.and T P1) T))) = ((λ.λ.and T P1) 1 ((λ.λ.and T P1) 2 T)) = ((λ.λ.and T P1) 1
T) = and T T = T

23. Experimentation
• maximum tree depth for λ abstraction = 4
• crossover rate = 100%
• primitives :

24. Experimentation
• maximum depth of nested recursion = 100
• simple example with depth = 2
foldr
+ [1,2,3]
foldr
+ [1,2,3]
0

25. Selection of fitness cases & error handling
• even-2-parity, as even patterns - 4 cases
• even-3-parity, as odd patterns - 8 cases
• total 12 cases
• is hoped that generated programs can work for any value of N
• error will occur during run-time by implying a function into a value
• we capture this kind of error by type system and exception
• using a flag to mark this solution for penalty during fitness evaluation

26. Fitness design
• each potential solution is evaluated against all of the fitness cases
• correct => 1
• incorrect => 0
• run-time error => 0.5
• computing the summation of all result
• thus, 0 ≤ fitness of a potential solution ≤ 12

27. Selection of cut-point
• because of the using of fold and λ abstract, a node with a less depth will have
a stronger description:
foldr
+ [1,2,3]
foldr
+ [1,2,3]
0
• adopting a method: node have a higher chance to be selected by crossover if
it is more close root

28. Crossover and mutation (1/2)
• by de Burjin denotation and type system
• we can explicit two useful informations during the major operation of GP
i. the number of parameters of function
ii.the type signature of function
• during crossover, the selection of a cut-point must be valid and reasonable
• i.e. both parents will exchange subtree with same type signature and
parameters’ number

29. Crossover and mutation (2/2)
• using the method in previous slide to select the point in first parent
• obtain some informations, for example: depth, type, parameter number, etc...
• using those informations to select the point in second parent

30. Experiment result (1/3)
• Fitness cases = 12
• start with 60 runs (initial individuals), population number = 60
• 57 (final individual) of them find a solution that work for any value of N

31. Experiment result (2/3)
• 57 correct generated
solutions
• exist 8 different programs

32. Experiment result (3/3)
• compare with GGP and GP with ADF
• can solve any value of N
• high success rate
• least requirement on minimum number of all generated individual
• fitness cases is small enough: (12 > 8) << 128
• less number of fitness procession
✓ ✓
✓ 95%
✓
✓
✓

33. Performance
• P(M,i) is the cumulative probability, M = population number, i = generation
• I(M, i, z) is the individual number, M = population number, i = generation, z is
the accuracy rate
• M = 500
• I(500, 3, 0.99) = 14,000
• i.e. as M = 500 and generation = 3, there exist a least number of total
individual = 14,000

34. Conclusion
• λ abstraction and fold can improve GP
• because original GP simulates structures and contents both, however, the
using of λ and fold can reduce the effort in structural evolution
• makes GP focus on contents only
• in other word, there use a higher-order methods to describe the syntactical
structure and remainder are semantical contents that can be found by GP