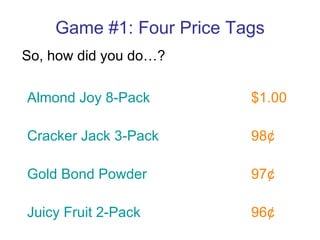
1. Game shows involve complex mathematical problems for both contestants and producers. Contestants must strategize their gameplay while producers aim to build entertaining yet profitable games.
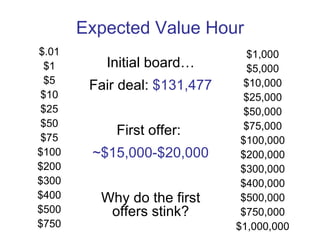
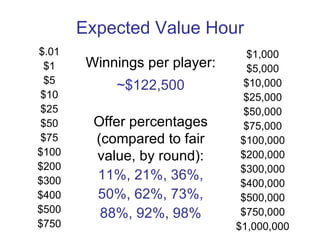
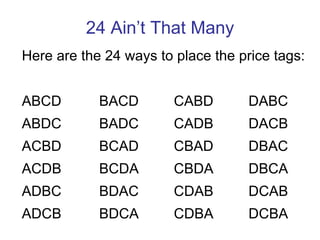
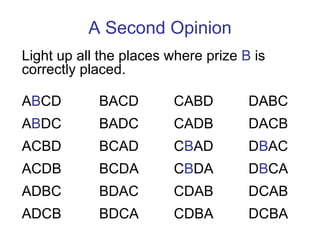
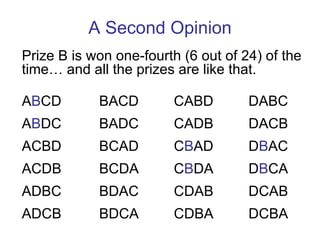
2. Common game show games like "The Price is Right" and "Deal or No Deal" can be analyzed using probability and expected value calculations to determine the optimal strategies for players and maximize producer profits.
3. Analyzing data from past episodes of popular game shows provides insights into real-world behaviors that can inform mathematical modeling of game dynamics.
![The Mathematics of Game Shows Bowen Kerins Senior Curriculum Designer, EDC (and part-time game consultant) [email_address]](https://image.slidesharecdn.com/gameshowsatmim2010-100113215903-phpapp02/75/Game-Show-Math-1-2048.jpg)












































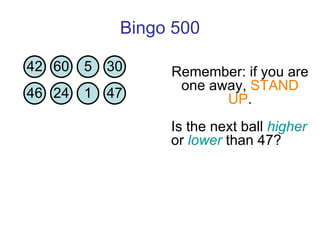
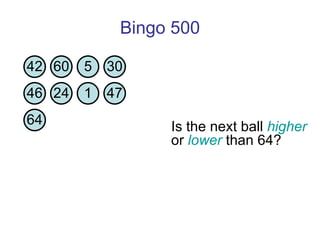
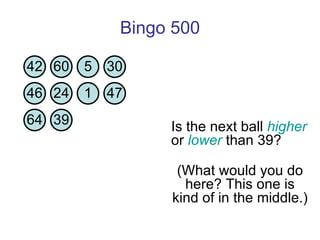
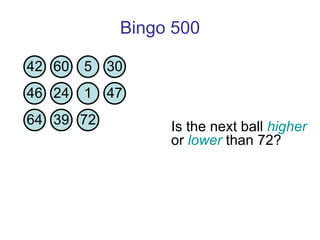
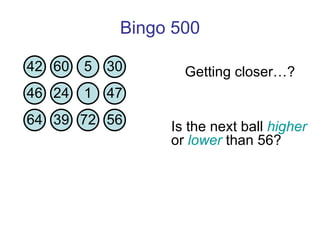
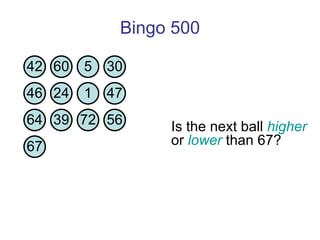
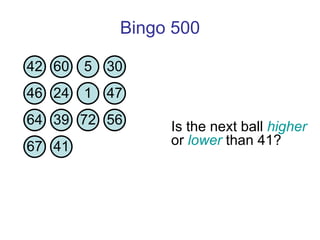
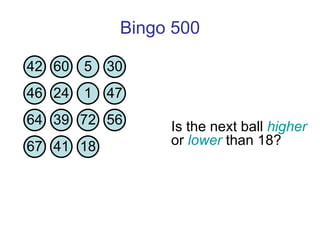
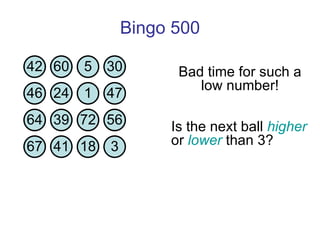
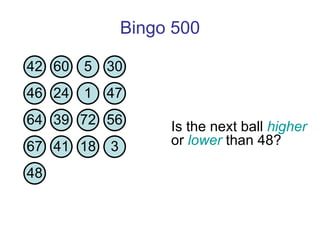
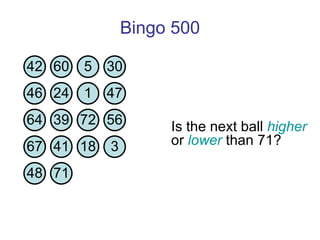
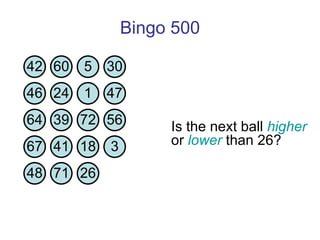


![Thanks and good luck! Any questions? Bowen Kerins Senior Curriculum Designer, EDC (and part-time game consultant) [email_address]](https://image.slidesharecdn.com/gameshowsatmim2010-100113215903-phpapp02/85/Game-Show-Math-81-320.jpg)