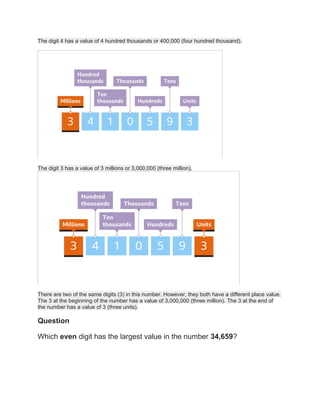
The document explains the concept of place value, detailing how the position of a digit in a number determines its value and aids in comparing and describing numbers. It also discusses positive and negative numbers, their representation on a number line, and the rules for adding, subtracting, multiplying, and dividing them. Real-world applications, including their uses in daily life and mathematics, are also highlighted.

1. NUMBER
Place Value
Key points

Place value describes the position of a digit in a number.

Numbers are part of everyday life. Understanding place value can help when
writing and describing numbers and carrying out simple calculations without
using a calculator.

Place value enables us to compare different values, e.g to compare high
scores when gaming.
What is place value?
Place value describes the position of a digit in a number. It also gives
the value of each digit in a number.

Whilst a digit in a number can be the same, its value depends on its position
within the number.

Knowing the place value of each digit can help when comparing numbers.

The order of place value of digits in a number from right to left is: units, tens,
hundreds, thousands, ten thousands, a hundred thousands, etc.

Units are often referred to as ones. E.g, 34 has 3 tens and 4 units, or we
could say 34 has 3 tens and 4 ones.
Example: place value

2. In the number 3,410,593 each digit represents a different place value.
The digit 3 has a value of 3 units or 3 (three).
The digit 9 has a value of 9 tens or 90 (ninety).

3. The digit 5 has a value of 5 hundreds or 500 (five hundred).
The digit 0 has a value of 0 thousands.
The digit 1 has a value of 1 ten thousands or 10,000 (ten thousand).

4. The digit 4 has a value of 4 hundred thousands or 400,000 (four hundred thousand).
The digit 3 has a value of 3 millions or 3,000,000 (three million).
There are two of the same digits (3) in this number. However, they both have a different place value.
The 3 at the beginning of the number has a value of 3,000,000 (three million). The 3 at the end of
the number has a value of 3 (three units).
Question
Which even digit has the largest value in the number 34,659?

5. Place value - writing and describing
whole numbers
Key points

Numbers can be written as digits or as words, eg 60 or sixty.

Understanding place value allows you to partition numbers in different
ways. This helps to deal with larger values more efficiently.

Place value can be used to compare and order integer values.
Writing numbers using place value
Whole numbers are a set of numbers including all positive integers
and 0. Whole numbers do not include fractions, decimals or negative
numbers.

When considering a larger number, using place value labels can often
help. Place value labels can be written as words or using digits. When
using words, units are often referred to as ones. Eg, 34 has 3 tens and
4 units, or we could say 34 has 3 tens and 4 ones.

When describing numbers, partition them according to their place
value. Partitioning numbers makes them easier to calculate with.

Some digits are 'joined' in their description. For example, the number
65 is not described as 'six tens and five units'. Instead, it is described
by the more common name of 'sixty-five'.
Example: using place value labels

6. Using place value, partition 65 into six tens and five units. This is written as sixty-five.
565 can be partitioned into five lots of 100, six lots of 10 and five units. 565 is written as five
hundred and sixty-five.
1,565 can be partitioned into one lot of 1,000, five lots of 100, six lots of 10 and five units. 1,565
is written as one thousand, five hundred and sixty-five.

7. 21,565 can be partitioned into two lots of 10,000, one lot of 1,000, five lots of 100, six lots of 10
and five units. 21,565 is written as twenty-one thousand, five hundred and sixty-five.
321,565 can be partitioned into three lots of 100,000, two lots of 10,000, one lot of 1,000, five
lots of 100, six lots of 10 and five units. 321,565 is written as three hundred and twenty-one
thousand, five hundred and sixty-five.

8. The number 5,321,565 can be written in words as five million, three hundred and twenty-one
thousand, five hundred and sixty-five.
Comparing numbers using place value

Place value can be used to compare two or more numbers.

Using place value can help to identify the largest number.

The place value of a digit increases by ten times each step to the left
and decreases by ten times each step to the right.
To compare numbers:
1. Start with the greatest place value. Compare the digits in the greatest
place value position.
2. If these digits are the same, continue to the next smaller place until the
digits are different.
Example: which number is greater?

9. Write the first number 4,567 using place value labels.
Write the second number 4,573 underneath using the same place value labels.

10. Compare the digits in the thousands place. The digit (4) is the same in each number.
Compare the digits in the hundreds place. The digit (5) is the same in each number.

11. Compare the digits in the tens place. The digits are different. 7 tens is greater than 6 tens.
The number 4,573 is greater than 4,567
Real-world maths
Place value for whole numbers is used regularly in daily life.
Sometimes numbers appear using digits or figures, but they can also
appear as words.

Numbers can appear as instructions in recipes, on a scale when
measuring quantities or as a price in shops or online.

12. 
Being able to compare numbers when shopping is important to make
sure you are getting a good deal. For example, comparing prices when
buying a car could save money.
Understanding place value can help to compare the prices of cars.
It is also used by different types of business such as car manufacturers
and shops.

A car manufacturer may want to compare different car models to see
which one makes the biggest profit.

A shop owner may want to order products in terms of how well they
sell. This is because how well they sell can affect where they position
each item within their shop.
Positive and Negative Numbers
Key points

Any number above zero is a positive number. Positive numbers can either
be written without a sign or with a + sign in front of them.

Any number below zero is a negative number. Negative numbers are always
written with a - sign in front of them.

Always look at the sign in front of a number to see if it is positive or negative.

Zero is neither positive nor negative. Learning about using a number line will
help you to understand this concept.
Positive and negative numbers
It may be useful to use a number line when representing both positive and
negative numbers.

13. 
Begin at zero.

For positive numbers, count to the right of zero. Positive numbers get
higher the further to the right, eg 6 is greater than 3

For negative numbers, count to the left of zero. Negative numbers get lower
the further to the left, eg -4 is less than -1

A number line can be split into different size steps.
Example: positive and negative numbers on a number line
When representing numbers, begin at zero.
To represent the value of -4, find zero. Then move 4 steps to the left.

14. To represent the value of -5, find zero. Then move 5 steps to the left.
To represent the value of 2, find zero. Then move 2 steps to the right.

15. A number line can be split into different size steps. Here each step is
worth 0.5 rather than a whole number.
Question
Which numbers are negative?
1, 0, -3, -4, 0.23, -1003, 7.2, -0.35 and -⅝
Key points

There are rules for adding and
subtracting positive and negative numbers.

If a number has no sign it usually means that it is a positive number.
For example, 7 is really +7

Learning how to use a number line may help you with calculations.
Adding and subtracting
When adding or subtracting negative numbers it can be useful to use
a number line.

To add and subtract numbers always begin counting from zero.

16. 
When adding positive numbers, count to the right.

When subtracting positive numbers, count to the left.
Example: calculate 4 – 6
To add and subtract numbers always begin counting from zero. When adding
positive numbers, count to the right. When subtracting positive numbers, count to
the left.
To work out 4 – 6, start at zero, then move 4 steps to the right. This is 4

17. Then move 6 places to the left. This shows that 4 – 6 = -2
Example: calculate (-6) + 8
Work out (-6) + 8

18. To work out (-6) + 8, start at zero. Move 6 steps to the left. This is -6
Then move 8 steps to the right. This shows that (-6) + 8 = 2
Example: calculate (-4) – 3

19. Work out (-4) – 3
To work out (-4) – 3, start at zero. Move 4 steps to the left. This is -4

20. Then move 3 more steps to the left. This shows that (-4) – 3 = -7
Real-world example
A thermometer is a number line that depicts temperature and often
uses a vertical number line rather than horizontal.
When reading a thermometer:

zero represents 0°C

plus temperatures are above zero, eg 8°C counting upwards as the
temperature gets warmer (positive numbers)

minus temperatures are below zero, eg -4°C counting downwards as
the temperature gets colder (negative numbers)
Question
In the example below, what is the difference between the daytime and
night-time temperatures?

21. How to multiply and divide positive
and negative numbers
Key points

Multiplication is commutative. This means that the order in which you
multiply a pair of numbers does not make a difference, eg 3 x 5 = 5 x 3

The product is the answer when two or more numbers are multiplied
together.

Calculations can be written with brackets around negative numbers
because this can make a calculation easier to read, eg -3 × -1 is the same
calculation as (-3) × (-1)

Learning about positive and negative numbers will help when
multiplying and dividing negative numbers.

22. Multiplying positive and negative numbers
When multiplying negative numbers it is often useful to complete the
calculation using positive numbers initially. Then remember that:

multiplying two numbers together with the same sign gives
a positive answer

multiplying two numbers together with different signs gives
a negative answer
Examples: multiplying positive and negative numbers
Start by completing the calculation using positive numbers first, then use the sign rules to
find the sign of the answer.

23. This multiplication table includes both positive and negative numbers. Follow the
pattern to see the effect of multiplying by negative numbers.
Calculate 3 × 2 initially to get 6, then remember that multiplying two numbers with
the same sign means the answer will be positive, (-3) × (-2) = +6

24. Calculate 3 × 3 initially to get 9, then remember that multiplying two numbers with
different signs means the answer will be negative, 3 x (-3) = -9
Dividing positive and negative numbers
When dividing negative numbers it is often useful to complete the
calculation using positive numbers initially. Remember that:

dividing two numbers with the same sign gives a positive answer

dividing two numbers with different signs gives a negative answer
Examples: dividing positive and negative numbers

25. Start by completing the calculation using positive numbers first, then use the sign rules to
find the sign of the answer.
Calculate 12 ÷ 4 initially to get 3, then remember that dividing two numbers with different
signs means the answer will be negative, 12 ÷ (-4) = -3

26. Calculate 32 ÷ 4 initially to get 8, then remember that dividing two numbers with different
signs means the answer will be negative, (-32) ÷ 4 = -8
Question
Calculate the following. You might need a pen and paper to note down
the answers.
1. (-6) × 3
2. (-4) × (-2)
3. (-6) ÷ 2
4. (-6) ÷ (-2)