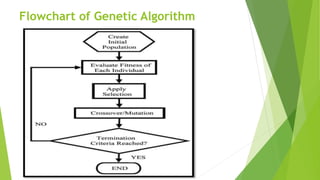
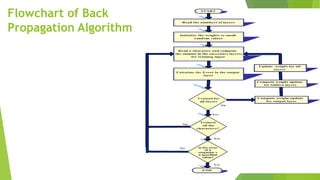
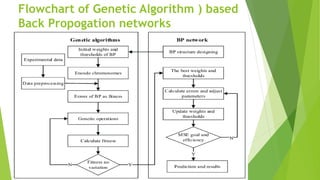
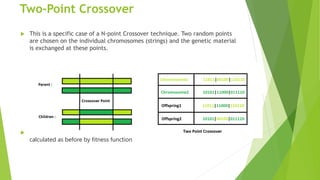
The document discusses the integration of genetic algorithms with back propagation networks to optimize weight extraction and training speed in artificial neural networks. It outlines the various components involved in this hybrid approach, including coding, weight extraction, fitness evaluation, reproduction, and convergence, and highlights the challenges such as vanishing gradients and the need for differentiable activation functions. The ultimate goal is to enhance the performance of neural networks by effectively guiding the optimization process through genetic algorithms.