This document contains 19 multiple choice questions about functions. The questions cover topics such as function graphs, polynomial functions, logarithmic functions, and inequalities involving functions. For each question there are 5 possible answer choices labeled a-e. The answers given are: 1) B 2) C 3) D 4) D 5) D 6) A 7) C 8) E 9) B 10) C 11) A 12) C 13) B 14) C 15) D 16) D 17) A 18) B 19) C.

1. LISTAS DE EXERCÍCIOS
FUNÇÕES

2. FUNÇÕES
1
01. (Unicamp 2015) A figura abaixo exibe o gráfico de uma função y f(x).
=
Então, o gráfico de y 2f(x 1)
= − é dado por
a) b) c) d)
02. (Insper 2015) A relação entre o investimento x (em milhões de reais) na propaganda para a divulgação de um
produto e o número k de potenciais consumidores (em milhões) atingidos por essa campanha é dada por uma função
k(x), cujo gráfico está representado a seguir.
Para avaliar o retorno dessa campanha, calculam-se dois índices, como se segue:
- identificam-se os valores 1
x , 2
x e 3
x para os quais 1, 2 e 4 milhões de potenciais consumidores são atingidos,
respectivamente;
- a razão 2
1
x
x
resulta no índice a
I ;
- a razão 3
2
x
x
resulta no índice b
I .
Para a função k(x) acima, o valor de
+
−
b a
b a
I I
I I
é
a) 2.
b) 3.
c) 4.
d) 5.
e) 6.

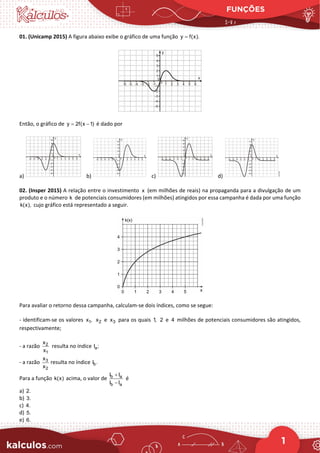
3. FUNÇÕES
2
03. (Mackenzie 2015) Sejam 𝑓𝑓: ℝ → ℝ e 𝑔𝑔: ℝ → ℝ funções definidas por
x x
2 2
f(x)
2
−
+
= e
x x
2 2
g(x) .
2
−
−
= Então,
podemos afirmar que
a) f é crescente e g é decrescente.
b) f e g se interceptam em x 0.
=
c) f(0) g(0).
= −
d) 2 2
[f(x)] [g(x)] 1.
− =
e) f(x) 0
≥ e g(x) 0,
≥ ∀ 𝑥𝑥 ∈ ℝ.
04. (Fatec 2015) “O número de deslocamentos de pessoas entre cidades paulistas dobrou em uma década, enquanto
o crescimento populacional foi de 1% ao ano. A pesquisa obtida pelo Estado considera viagens feitas por maiores de
15 anos na macrometrópole paulista – 173 municípios entre a Baixada Santista e o Vale do Paraíba, passando por
São Paulo, Campinas e São José dos Campos.” A notícia revela um fenômeno social chamado migração pendular, que
ocorre quando pessoas se deslocam entre diferentes cidades diariamente para trabalhar ou estudar. Suponha que,
nos próximos anos, o número de deslocamentos de pessoas entre cidades paulistas continue dobrando a cada década
e que o crescimento populacional continue aumentando à taxa de 1% ao ano. Com base nessas suposições, podemos
afirmar corretamente que
a) o crescimento dos deslocamentos será linear, enquanto que o crescimento populacional será exponencial.
b) o crescimento dos deslocamentos será logarítmico, enquanto que o crescimento populacional será linear.
c) o crescimento dos deslocamentos será exponencial, enquanto que o crescimento populacional será linear.
d) tanto o crescimento dos deslocamentos quanto o crescimento populacional serão exponenciais.
e) tanto o crescimento dos deslocamentos quanto o crescimento populacional serão lineares.
05. (Insper 2015) Uma operadora de telefonia celular oferece a seus clientes dois planos:
Superminutos: o cliente paga uma tarifa fixa de R$ 100,00 por mês para os primeiros 200 minutos que utilizar. Caso
tenha consumido mais minutos, irá pagar R$ 0,60 para cada minuto que usou a mais do que 200.
Supertarifa: o cliente paga R$ 60,00 de assinatura mensal mais R$ 0,40 por minuto utilizado.
Todos os meses, o sistema da operadora ajusta a conta de cada um de seus clientes para o plano mais barato, de
acordo com as quantidades de minutos utilizadas. Nesse modelo, o plano Superminutos certamente será selecionado
para consumidores que usarem
a) menos do que 60 minutos no mês.
b) entre 40 e 220 minutos no mês.
c) entre 60 e 300 minutos no mês.
d) entre 100 e 400 minutos no mês.
e) mais do que 400 minutos no mês.
06. (Insper 2015) Os ingressos para a pré-estreia mundial de um filme começaram a ser vendidos 20 dias antes da
exibição do filme, sendo que:
- nos 10 primeiros dias desse período, as vendas foram feitas exclusivamente nas bilheterias;
- nos dez últimos dias, as vendas ocorreram simultaneamente nas bilheterias e pela internet.
Considere que t representa o tempo, em dias, desde o início das vendas e v(t) o total de ingressos vendidos, em
milhões, até o tempo t. No período de vendas simultâneas nas bilheterias e pela internet, a função v(t) é dada por:
=
− + −
2
v(t) 0,1t 4t 10. O número de ingressos vendidos apenas nos 10 dias que antecederam a exibição do filme foi
a) 10 milhões b) 20 milhões c) 30 milhões d) 40 milhões e) 50 milhões

4. FUNÇÕES
3
07. (Insper 2015) Durante as vendas exclusivas nas bilheterias, a capacidade de atendimento dos guichês dos cinemas
do mundo todo, ao longo do tempo, era sempre a mesma, totalizando a venda de 2 milhões de ingressos por dia.
Assim, o gráfico que melhor descreve v(t) para esse período, em função de t, é
a) b) c) d) e)
08. (Insper 2015) Considere o polinômio dado por 3 2
p(x) x x 22x 40.
= − − + A figura a seguir mostra parte do gráfico
da função f, dada por f(x) p(x),
α
= ⋅ em que α é um número real.
A diferença entre a maior e a menor raiz de p(x) é igual a
a) 5.
b) 6.
c) 7.
d) 8.
e) 9.

5. FUNÇÕES
4
09. (Insper 2015) Informação I
A figura a seguir exibe parte do gráfico da função 0,85
f(x) log x,
= cujo domínio é {𝑥𝑥 ∈ ℝ|0 < 𝑥𝑥 ≤ 0,85}.
Informação II
Um carro, que no ato da compra vale R$ 40.000,00, tem uma desvalorização de 15% ao ano. Ou seja, após um ano,
o carro tem, a cada instante, um valor 15% menor do que o valor que tinha exatamente um ano antes. Passados 20
anos, o carro valerá cerca de
a) R$ 600,00. b) R$ 1.600,00. c) R$ 6.000,00. d) R$ 16.000,00. e) R$ 25.000,00.
10. (Insper 2014) A figura abaixo mostra o gráfico do polinômio P(x), de 5° grau e coeficientes reais, que apresenta
uma única raiz real.
O número de raízes reais do polinômio Q(x), dado, para todo x real, pela expressão Q(x) 2 P(x),
= − é igual a
a) 1 b) 2 c) 3 d) 4 e) 5

6. FUNÇÕES
5
11. (Insper 2014) Sendo k uma constante real positiva, considere o gráfico do polinômio de 3° grau P(x), mostrado na
figura.
Dentre as figuras a seguir, a única que pode representar o gráfico da função Q(x), definida, para todo x 0,
≠ pela lei
P(x)
Q(x)
x
= é
a) b) c) d) e)
12. (Mackenzie 2014) Se o polinômio de segundo grau 2
P(x) Ax Bx C
= + + é tal que P(1) 3,
= P(2) 11
= e P(4) 45,
= o
valor de B é
a) 0
b) 1
c) 1
−
d) 2
−
e) 5
−
13. (Insper 2014) Um leitor enviou a uma revista a seguinte análise de um livro recém-lançado, de 400 páginas:
“O livro é eletrizante, muito envolvente mesmo! A cada página terminada, mais rápido eu lia a próxima! Não conseguia
parar!”
Dentre os gráficos apresentados abaixo, o único que poderia representar o número de páginas lidas pelo leitor (N) em
função do tempo (t) de modo a refletir corretamente a análise feita é
a) b) c) d) e)

7. FUNÇÕES
6
14. (Mackenzie 2014) Se a função 𝑓𝑓: ℝ → ℝ é definida por x
f(x) | 3 1|,
= − a afirmação correta sobre f é
a) 𝐷𝐷(𝑓𝑓) = ℝ𝑒𝑒 𝐼𝐼𝐼𝐼(𝑓𝑓) = ℝ.
b) f é uma função crescente para todo x real.
c) f não é injetora nem sobrejetora.
d) f é injetora mas não é sobrejetora.
e) 𝐼𝐼𝐼𝐼 (𝑓𝑓) = ℝ+
∗
.
15. (Mackenzie 2014) Se 1 x
f(x) 3 +
= e g(x) sen x
= são duas funções definidas em ℝ, então os conjuntos de f g
 e
g f
 são, respectivamente,
a) ℝ+ e ℝ
b) ℝ+
∗
e ℝ
c) ℝ e [ ]
1, 9
−
d) [ ]
1, 9 e [ ]
1, 1
−
e) ℝ+
∗
e [ ]
1, 1
−
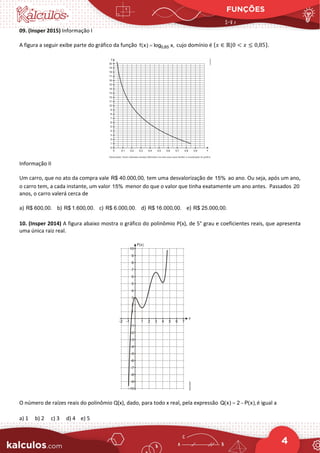
16. (Unicamp 2014) Considere as funções f e g, cujos gráficos estão representados na figura abaixo.
O valor de f(g(1)) g(f(1))
− é igual a
a) 0
b) – 1
c) 2
d) 1

8. FUNÇÕES
7
17. (Insper 2014) Analisando o comportamento das vendas de determinado produto em diferentes cidades, durante
um ano, um economista estimou que a quantidade vendida desse produto em um mês (Q), em milhares de unidades,
depende do seu preço (P), em reais, de acordo com a relação 2P
Q 1 4 (0,8) .
= + ⋅ No entanto, em Economia, é mais
usual, nesse tipo de relação, escrever o preço P em função da quantidade Q. Dessa forma, isolando a variável P na
relação fornecida acima, o economista obteve
a) 0,8
Q 1
P log .
4
−
=
b) 0,8
Q 1
P log .
8
−
 
=  
 
c) 0,8 Q 1
P 0,5 .
4
−
= ⋅
d) 0,8 Q 1
P .
8
−
=
e) 0,8
Q
P 0,5 log 1 .
4
 
=
⋅ −
 
 
18. (Unicamp 2014) O gráfico abaixo exibe a curva de potencial biótico q(t) para uma população de micro-organismos,
ao longo do tempo t.
Sendo a e b constantes reais, a função que pode representar esse potencial é
a) q(t) at b.
= +
b) t
q(t) a b .
=
c) 2
q(t) at bt.
= +
d) b
q(t) a log t.
= +

9. FUNÇÕES
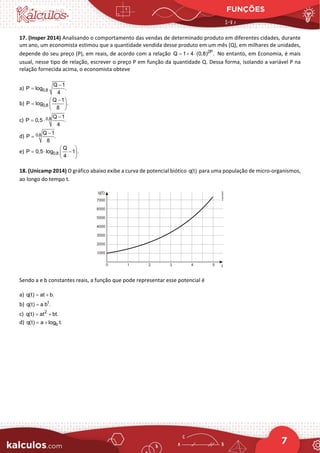
8
19. (Unesp 2014) Os gráficos de duas funções f(x) e g(x), definidas de ℝ em ℝ, estão representados no mesmo plano
cartesiano.
No intervalo [– 4, 5], o conjunto solução da inequação f(x) g(x) 0
⋅ < é
a) {𝑥𝑥 ∈ ℝ/−1 < 𝑥𝑥 < 3}.
b) {𝑥𝑥 ∈ ℝ/−1 < 𝑥𝑥 < 0𝑜𝑜𝑜𝑜3 < 𝑥𝑥 ≤ 5}
c) {𝑥𝑥 ∈ ℝ/−4 ≤ 𝑥𝑥 < −1𝑜𝑜𝑜𝑜0 < 𝑥𝑥 < 3}.
d) {𝑥𝑥 ∈ ℝ/−4 < 𝑥𝑥 < 0}.
e) {𝑥𝑥 ∈ ℝ/−4 ≤ 𝑥𝑥 < −1𝑜𝑜𝑜𝑜3 < 𝑥𝑥 < 5}.
GABARITO
1 - B 2 - C 3 - D 4 - D 5 - D
6 - A 7 - C 8 - E 9 - B 10 - C
11 - A 12 - C 13 - B 14 - C 15 - D
16 - D 17 - A 18 - B 19 - C