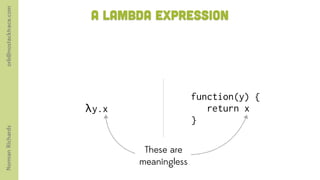
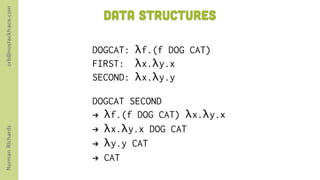
The document discusses the lambda calculus and its relationship to functional programming and JavaScript. It introduces Alonzo Church as the creator of lambda calculus and its use as the basis for functional programming. It then provides examples of lambda expressions, applications, and combinators to illustrate core concepts in lambda calculus and how it enables Turing completeness.