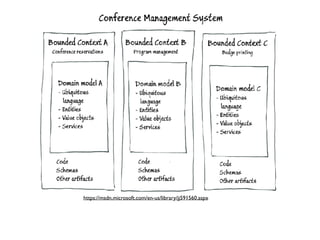
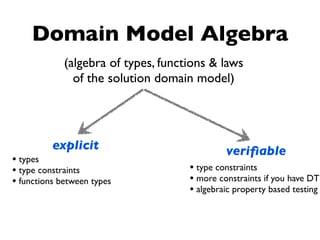
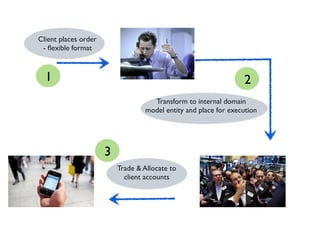
The document discusses functional and algebraic domain modeling. It defines an algebraic structure as a set with operations that satisfy axioms. Domain modeling involves identifying types, functions between types, and rules that govern the domain. A bounded context models a consistent vocabulary and behaviors as functions on domain objects. The algebra of a type refers to the number of possible inhabitants based on its structure. Product and sum types are discussed as ways to model heterogeneous data. Algebras of types and functions can be composed to build larger behaviors by following type relationships. An approach to domain modeling uses algebraic composition of identified behaviors to implement and modularize domain models.



















![Domain Model = ∪(i) Bounded Context(i)
Bounded Context = { m[T1,T2,..] | T(i) ∈ Types }
Module = { f(x,y,..) | p(x,y) ∈ Domain Rules }
• domain function
• on an object of types x, y, ..
• composes with other functions
• closed under composition
• business rules](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-21-320.jpg)







![Product Types in Scala
type Point = (Int, Int)
val p = (10, 12)
case class Account(no: String,
name: String,
address: String,
dateOfOpening: Date,
dateOfClosing: Option[Date]
)](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-30-320.jpg)





![sealed trait InstrumentType
case object CCY extends InstrumentType
case object EQ extends InstrumentType
case object FI extends InstrumentType
sealed trait Instrument {
def instrumentType: InstrumentType
}
case class Equity(isin: String, name: String, issueDate: Date,
faceValue: Amount) extends Instrument {
final val instrumentType = EQ
}
case class FixedIncome(isin: String, name: String, issueDate: Date,
maturityDate: Option[Date], nominal: Amount) extends Instrument {
final val instrumentType = FI
}
case class Currency(isin: String) extends Instrument {
final val instrumentType = CCY
}](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-36-320.jpg)












![Domain Model = ∪(i) Bounded Context(i)
Bounded Context = { m[T1,T2,..] | T(i) ∈ Types }
Module = { f(x,y,..) | p(x,y) ∈ Domain Rules }
• domain function
• on an object of types x, y
• composes with other functions
• closed under composition
• business rules](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-49-320.jpg)
![Domain Model = ∪(i) Bounded Context(i)
Bounded Context = { m[T1,T2,..] | T(i) ∈ Types }
Module = { f(x,y,..) | p(x,y) ∈ Domain Rules }
• domain function
• on an object of types x, y
• composes with other functions
• closed under composition
• business rules
Domain Algebra
Domain Algebra](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-50-320.jpg)



![def fromClientOrder: ClientOrder => Order
def execute(market: Market, brokerAccount: Account)
: Order => List[Execution]
def allocate(accounts: List[Account])
: List[Execution] => List[Trade]
trait Trading {
}
trait TradeComponent extends Trading
with Logging with Auditing
algebra of domain
behaviors / functions
functions aggregate
upwards into modules
modules aggregate
into larger modules](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-55-320.jpg)










![Option[A]
Either[A,B]
(partiality)
(disjunction)
List[A]
(non-determinism)
Reader[E,A]
(read from environment aka dependency Injection)
Writer[W,A]
(logging)
State[S,A]
(state management)
IO[A]
(external side-effects)
.. and there are many many more ..](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-66-320.jpg)
![F[A]
The answer that the
effect computesThe additional stuff
modeling the computation](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-67-320.jpg)
![• The F[_] that we saw is an opaque type - it
has no denotation till we give it one
• The denotation that we give to F[_] depends
on the semantics of compositionality that we
would like to have for our domain model
behaviors](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-68-320.jpg)
![def fromClientOrder: ClientOrder => F[Order]
def execute(market: Market, brokerAccount: Account)
: Order => F[List[Execution]]
def allocate(accounts: List[Account])
: List[Execution] => F[List[Trade]]
trait Trading[F[_]] {
}
Effect Type](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-69-320.jpg)
![• Just the Algebra
• No denotation, no
concrete type
• Explicitly stating that we
have effectful functions
here
def fromClientOrder: ClientOrder => F[Order]
def execute(market: Market, brokerAccount: Account)
: Order => F[List[Execution]]
def allocate(accounts: List[Account])
: List[Execution] => F[List[Trade]]
trait Trading[F[_]] {
}
Effect Type](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-70-320.jpg)

![The Program
def tradeGeneration[M[_]: Monad](T: Trading[M]) = for {
order <- T.fromClientOrder(cor)
executions <- T.execute(m1, ba, order)
trades <- T.allocate(List(ca1, ca2, ca3), executions)
} yield trades](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-72-320.jpg)
![class TradingInterpreter[F[_]]
(implicit me: MonadError[F, Throwable])
extends Trading[F] {
def fromClientOrder: ClientOrder => F[Order] = makeOrder(_) match {
case Left(dv) => me.raiseError(new Exception(dv.message))
case Right(o) => o.pure[F]
}
def execute(market: Market, brokerAccount: Account)
: Order => F[List[Execution]] = ...
def allocate(accounts: List[Account])
: List[Execution] => F[List[Trade]] = ...
}
One Sample Interpreter](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-73-320.jpg)

![The Program
def tradeGeneration[M[_]: Monad](T: Trading[M]) = for {
order <- T.fromClientOrder(cor)
executions <- T.execute(m1, ba, order)
trades <- T.allocate(List(ca1, ca2, ca3), executions)
} yield trades
import cats.effect.IO
object TradingComponent extends TradingInterpreter[IO]
tradeGeneration(TradingComponent).unsafeRunSync](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-75-320.jpg)
![The Program
def tradeGeneration[M[_]: Monad](T: Trading[M]) = for {
order <- T.fromClientOrder(cor)
executions <- T.execute(m1, ba, order)
trades <- T.allocate(List(ca1, ca2, ca3), executions)
} yield trades
import monix.eval.Task
object TradingComponent extends TradingInterpreter[Task]
tradeGeneration(TradingComponent)](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-76-320.jpg)
![The Program
def tradeGenerationLoggable[M[_]: Monad]
(T: Trading[M], L: Logging[M]) = for {
_ <- L.info("starting order processing")
order <- T.fromClientOrder(cor)
executions <- T.execute(m1, ba, order)
trades <- T.allocate(List(ca1, ca2, ca3), executions)
_ <- L.info("allocation done")
} yield trades
object TradingComponent extends TradingInterpreter[IO]
object LoggingComponent extends LoggingInterpreter[IO]
tradeGenerationLoggable(TradingComponent, LoggingComponent).unsafeRunSync](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-77-320.jpg)
![Raise the level of
abstraction
trait Trading[F[_]] {
def fromClientOrder
: Kleisli[F, ClientOrder, Order]
def execute(market: Market, brokerAccount: Account)
: Kleisli[F, Order, List[Execution]]
def allocate(accounts: List[Account])
: Kleisli[F, List[Execution], List[Trade]]
}](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-78-320.jpg)
![The Program
def tradeGeneration[M[_]: Monad](T: Trading[M])
: Kleisli[M, ClientOrder, List[Trade]] = {
T.fromClientOrder andThen
T.execute(m1, ba) andThen
T.allocate(List(ca1, ca2, ca3))
}
object TradingComponent extends TradingInterpreter[IO]
val tk = tradeGeneration(TradingComponent)
tk(cor).unsafeRunSync](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-79-320.jpg)








![• All names are from the domain vocabulary
• Just the algebra describing the promise, no
implementation details
• Purpose and effect explicit - yes, literally
explicit with effects
def fromClientOrder: ClientOrder => F[Order]
def execute(market: Market, brokerAccount: Account)
: Order => F[List[Execution]]
def allocate(accounts: List[Account])
: List[Execution] => F[List[Trade]]
trait Trading[F[_]] {
}](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-88-320.jpg)

![def tradeGeneration[M[_]: Monad](T: Trading[M]) = for {
order <- T.fromClientOrder(cor)
executions <- T.execute(m1, ba, order)
trades <- T.allocate(List(ca1, ca2, ca3), executions)
} yield trades
• The program tradeGeneration is completely side-effect free. It
generates a pure value.
• Since the program is pure, you can interpret it in many ways (as we saw
earlier).
• The side-effects occur only when you submit the program to the run time
system.
• This is also an example where using algebraic & functional approach we
get a clear separation between the building of an abstraction and
executing it.](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-90-320.jpg)

![trait Semigroup[A] {
def combine(x: A, y: A): A
}
trait Monoid[A] extends Semigroup[A] {
def empty: A
}
• With algebraic modeling, you can encode the closure of operations
through the algebra of a Monoid.
★ parametric
★ define the algebra once, implement it as many times based on the
context
★ compositionality at the algebra level
• For stateful computation, use the algebra of the State Monad and
manipulate state as a Monoid](https://image.slidesharecdn.com/functional-algebraic-domain-modeling-180201213343/85/Functional-and-Algebraic-Domain-Modeling-92-320.jpg)

