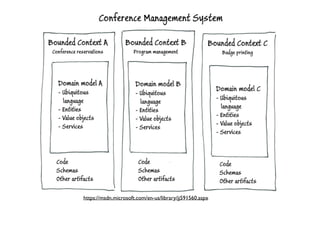
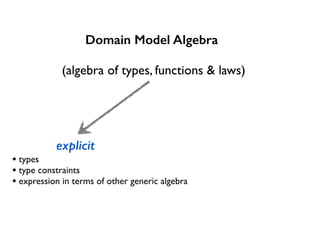
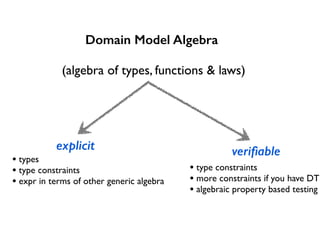
An algebraic approach to functional domain modeling is presented where: 1. The domain model is represented as a collection of functions operating on algebraic data types that represent domain entities. 2. These functions are organized into bounded contexts that group related behaviors and are parameterized on types. 3. The domain model is defined as an algebra of types, functions, and laws/rules through a domain algebra. This algebra can then have multiple implementations. 4. An example domain algebra for a trading system is defined using Kleisli arrows to model functions with effects like ordering and execution. The complete trade generation logic is implemented by composing these functions algebraically.

1. An Algebraic Approach to Functional
Domain Modeling
Debasish Ghosh
@debasishg
Functional Conf 2016

2. Domain Modeling

3. Domain Modeling(Functional)

4. What is a domain model ?
A domain model in problem solving and software engineering is a
conceptual model of all the topics related to a specific problem. It
describes the various entities, their attributes, roles, and
relationships, plus the constraints that govern the problem domain.
It does not describe the solutions to the problem.
Wikipedia (http://en.wikipedia.org/wiki/Domain_model)

5. The Functional Lens ..
“domain API evolution through algebraic
composition”

6. The Functional Lens ..
“domain API evolution through algebraic
composition”
Building larger domain behaviours
out of smaller ones

7. The Functional Lens ..
“domain API evolution through algebraic
composition”
Use composition
of pure functions and types

12. Your domain model is a
function

13. Your domain model is a
function

14. Your domain model is a
collection of functions

15. Your domain model is a
collection of functions
some simpler models are ..

16. https://msdn.microsoft.com/en-us/library/jj591560.aspx

17. A Bounded Context
• has a consistent vocabulary
• a set of domain behaviours modelled as
functions on domain objects
implemented as types
• each of the behaviours honour a set of
business rules
• related behaviors grouped as modules

18. Domain Model = ∪(i) Bounded Context(i)

19. Domain Model = ∪(i) Bounded Context(i)
Bounded Context = { m[T1,T2,..] | T(i) ∈ Types }
• a module parameterised
on a set of types

20. Domain Model = ∪(i) Bounded Context(i)
Bounded Context = { m[T1,T2,..] | T(i) ∈ Types }
Module = { f(x) | p(x) ∈ Domain Rules }
• domain function
• on an object of type x
• composes with other functions
• closed under composition
• business rules

21. • Functions / Morphisms
• Types / Sets
• Composition
• Rules / Laws

22. • Functions / Morphisms
• Types / Sets
• Composition
• Rules / Laws
algebra

23. Domain Model Algebra

24. Domain Model Algebra
(algebra of types, functions & laws)

25. Domain Model Algebra
(algebra of types, functions & laws)
explicit
• types
• type constraints
• expression in terms of other generic algebra

26. Domain Model Algebra
(algebra of types, functions & laws)
explicit verifiable
• types
• type constraints
• expr in terms of other generic algebra
• type constraints
• more constraints if you have DT
• algebraic property based testing

27. Problem Domain

28. Bank
Account
Trade
Customer
...
...
...
Problem Domain
...
entities

29. Bank
Account
Trade
Customer
...
...
...
do trade
process
execution
place
order
Problem Domain
...
entities
behaviors

30. Bank
Account
Trade
Customer
...
...
...
do trade
process
execution
place
order
Problem Domain
...
market
regulations
tax laws
brokerage
commission
rates
...
entities
behaviors
laws

31. do trade
process
execution
place
order
Solution Domain
...
behaviors
Functions
([Type] => Type)

32. Bank
Account
Trade
Customer
...
...
...
do trade
process
execution
place
order
Solution Domain
...
entities
behaviors
functions
([Type] => Type)
algebraic data type

33. Bank
Account
Trade
Customer
...
...
...
do trade
process
execution
place
order
Solution Domain
...
market
regulations
tax laws
brokerage
commission
rates
...
entities
behaviors
laws
functions
([Type] => Type)
algebraic data type business rules / invariants

34. Bank
Account
Trade
Customer
...
...
...
do trade
process
execution
place
order
Solution Domain
...
market
regulations
tax laws
brokerage
commission
rates
...
entities
behaviors
laws
functions
([Type] => Type)
algebraic data type business rules / invariants
Monoid
Monad
...

35. Bank
Account
Trade
Customer
...
...
...
do trade
process
execution
place
order
Solution Domain
...
market
regulations
tax laws
brokerage
commission
rates
...
entities
behaviors
laws
functions
([Type] => Type)
algebraic data type business rules / invariants
Monoid
Monad
...
Domain Algebra

36. Domain Model = ∪(i) Bounded Context(i)
Bounded Context = { m[T1,T2,..] | T(i) ∈ Types }
Module = { f(x) | p(x) ∈ Domain Rules }
• domain function
• on an object of type x
• composes with other functions
• closed under composition
• business rules
Domain Algebra
Domain Algebra

37. Client places order
- flexible format
1

38. Client places order
- flexible format
Transform to internal domain
model entity and place for execution
1 2

39. Client places order
- flexible format
Transform to internal domain
model entity and place for execution
Trade & Allocate to
client accounts
1 2
3

40. def clientOrders: ClientOrderSheet => List[Order]
def execute: Market => Account => Order => List[Execution]
def allocate: List[Account] => Execution => List[Trade]

41. def clientOrders: ClientOrderSheet => List[Order]
def execute[Account <: BrokerAccount]: Market => Account
=> Order => List[Execution]
def allocate[Account <: TradingAccount]: List[Account]
=> Execution => List[Trade]

42. def clientOrders: ClientOrderSheet => List[Order]
def execute: Market => Account => Order => List[Execution]
def allocate: List[Account] => Execution => List[Trade]
Types out of thin air No implementation till now
Type names resonate domain language

43. def clientOrders: ClientOrderSheet => List[Order]
def execute: Market => Account => Order => List[Execution]
def allocate: List[Account] => Execution => List[Trade]
•Types (domain entities)
• Functions operating on types (domain behaviors)
• Laws (business rules)

44. def clientOrders: ClientOrderSheet => List[Order]
def execute: Market => Account => Order => List[Execution]
def allocate: List[Account] => Execution => List[Trade]
•Types (domain entities)
• Functions operating on types (domain behaviors)
• Laws (business rules)
Algebra of the API

45. trait Trading[Account, Trade, ClientOrderSheet, Order,
Execution, Market] {
def clientOrders: ClientOrderSheet => List[Order]
def execute: Market => Account => Order => List[Execution]
def allocate: List[Account] => Execution => List[Trade]
def tradeGeneration(market: Market, broker: Account,
clientAccounts: List[Account]) = ???
}
parameterized on typesmodule

46. Algebraic Design
• The algebra is the binding contract of the
API
• Implementation is NOT part of the
algebra
• An algebra can have multiple interpreters
(aka implementations)
• One of the core principles of functional
programming is to decouple the algebra
from the interpreter

47. def clientOrders: ClientOrderSheet => List[Order]
def execute: Market => Account => Order => List[Execution]
def allocate: List[Account] => Execution => List[Trade]
let’s do some algebra ..

48. def clientOrders: ClientOrderSheet => List[Order]
def execute(m: Market, broker: Account): Order => List[Execution]
def allocate(accounts: List[Account]): Execution => List[Trade]
let’s do some algebra ..

49. def clientOrders: ClientOrderSheet => List[Order]
def execute(m: Market, broker: Account): Order => List[Execution]
def allocate(accounts: List[Account]): Execution => List[Trade]
let’s do some algebra ..

50. def clientOrders: ClientOrderSheet => List[Order]
def execute(m: Market, broker: Account): Order => List[Execution]
def allocate(accounts: List[Account]): Execution => List[Trade]
let’s do some algebra ..

51. def clientOrders: ClientOrderSheet => List[Order]
def execute(m: Market, broker: Account): Order => List[Execution]
def allocate(accounts: List[Account]): Execution => List[Trade]
let’s do some algebra ..

52. def clientOrders: ClientOrderSheet => List[Order]
def execute(m: Market, broker: Account): Order => List[Execution]
def allocate(accounts: List[Account]): Execution => List[Trade]
let’s do some algebra ..

53. def f: A => List[B]
def g: B => List[C]
def h: C => List[D]
.. a problem of composition ..

54. .. a problem of composition
with effects ..
def f: A => List[B]
def g: B => List[C]
def h: C => List[D]

55. def f[M: Monad]: A => M[B]
def g[M: Monad]: B => M[C]
def h[M: Monad]: C => M[D]
.. a problem of composition with effects
that can be generalized ..

56. case class Kleisli[M[_], A, B](run: A => M[B]) {
def andThen[C](f: B => M[C])
(implicit M: Monad[M]): Kleisli[M, A, C] =
Kleisli((a: A) => M.flatMap(run(a))(f))
}
.. function composition with Effects ..
It’s a Kleisli !

57. def clientOrders: Kleisli[List, ClientOrderSheet, Order]
def execute(m: Market, b: Account): Kleisli[List, Order, Execution]
def allocate(acts: List[Account]): Kleisli[List, Execution, Trade]
Follow the types
.. function composition with Effects ..
def clientOrders: ClientOrderSheet => List[Order]
def execute(m: Market, broker: Account): Order => List[Execution]
def allocate(accounts: List[Account]): Execution => List[Trade]

58. def clientOrders: Kleisli[List, ClientOrderSheet, Order]
def execute(m: Market, b: Account): Kleisli[List, Order, Execution]
def allocate(acts: List[Account]): Kleisli[List, Execution, Trade]
Domain algebra composed with the categorical
algebra of a Kleisli Arrow
.. function composition with Effects ..

59. def clientOrders: Kleisli[List, ClientOrderSheet, Order]
def execute(m: Market, b: Account): Kleisli[List, Order, Execution]
def allocate(acts: List[Account]): Kleisli[List, Execution, Trade]
.. that implements the semantics of our domain
algebraically ..
.. function composition with Effects ..

60. def tradeGeneration(
market: Market,
broker: Account,
clientAccounts: List[Account]) = {
clientOrders andThen
execute(market, broker) andThen
allocate(clientAccounts)
}
Implementation follows the specification
.. the complete trade generation logic ..

61. def tradeGeneration(
market: Market,
broker: Account,
clientAccounts: List[Account]) = {
clientOrders andThen
execute(market, broker) andThen
allocate(clientAccounts)
}
Implementation follows the specification and we
get the Ubiquitous Language for free :-)
.. the complete trade generation logic ..

62. algebraic & functional
• Just Pure Functions. Lower cognitive load -
don’t have to think of the classes & data
members where behaviors will reside
• Compositional. Algebras compose - we
defined the algebras of our domain APIs in
terms of existing, time tested algebras of
Kleislis and Monads

63. def clientOrders: Kleisli[List, ClientOrderSheet, Order]
def execute(m: Market, b: Account): Kleisli[List, Order, Execution]
def allocate(acts: List[Account]): Kleisli[List, Execution, Trade]
.. our algebra still doesn’t allow customisable
handling of errors that may occur within our
domain behaviors ..
.. function composition with Effects ..

64. more algebra,
more types

65. def clientOrders: Kleisli[List, ClientOrderSheet, Order]
return type constructor

66. def clientOrders: Kleisli[List, ClientOrderSheet, Order]
return type constructor
What happens in case the operation fails ?

67. Error handling as an
Effect
• pure and functional
• with an explicit and published algebra
• stackable with existing effects
def clientOrders: Kleisli[List, ClientOrderSheet, Order]

68. def clientOrders: Kleisli[List, ClientOrderSheet, Order]
.. stacking of effects ..
M[List[_]]

69. def clientOrders: Kleisli[List, ClientOrderSheet, Order]
.. stacking of effects ..
M[List[_]]: M is a Monad

70. type Response[A] = String / Option[A]
val count: Response[Int] = some(10).right
for {
maybeCount <- count
} yield {
for {
c <- maybeCount
// use c
} yield c
}
Monad Transformers

71. type Response[A] = String / Option[A]
val count: Response[Int] = some(10).right
for {
maybeCount <- count
} yield {
for {
c <- maybeCount
// use c
} yield c
}
type Error[A] = String / A
type Response[A] = OptionT[Error, A]
val count: Response[Int] = 10.point[Response]
for{
c <- count
// use c : c is an Int here
} yield (())
Monad Transformers

72. type Response[A] = String / Option[A]
val count: Response[Int] = some(10).right
for {
maybeCount <- count
} yield {
for {
c <- maybeCount
// use c
} yield c
}
type Error[A] = String / A
type Response[A] = OptionT[Error, A]
val count: Response[Int] = 10.point[Response]
for{
c <- count
// use c : c is an Int here
} yield (())
Monad Transformers
richer algebra

73. Monad Transformers
• collapses the stack and gives us a single
monad to deal with
• order of stacking is important though

74. def clientOrders: Kleisli[List, ClientOrderSheet, Order]
.. stacking of effects ..
case class ListT[M[_], A] (run: M[List[A]]) { //..

75. type StringOr[A] = String / A
type Valid[A] = ListT[StringOr, A]
def clientOrders: Kleisli[Valid, ClientOrderSheet, Order]
def execute(m: Market, b: Account): Kleisli[Valid, Order, Execution]
def allocate(acts: List[Account]): Kleisli[Valid, Execution, Trade]
.. a small change in algebra, a huge step
for our domain model ..

76. def execute(market: Market, brokerAccount: Account) =
kleisli[List, Order, Execution] { order =>
order.items.map { item =>
Execution(brokerAccount, market, ..)
}
}

77. private def makeExecution(brokerAccount: Account,
item: LineItem, market: Market): String / Execution = //..
def execute(market: Market, brokerAccount: Account) =
kleisli[Valid, Order, Execution] { order =>
listT[StringOr](
order.items.map { item =>
makeExecution(brokerAccount, market, ..)
}.sequenceU
)
}

78. List
(aggregates)
Algebra of types

79. List
(aggregates)
Disjunction
(error accumulation)
Algebra of types

80. List
(aggregates)
Disjunction
(error accumulation)
Kleisli
(dependency injection)
Algebra of types

81. List
(aggregates)
Disjunction
(error accumulation)
Kleisli
(dependency injection)
Future
(reactive non-blocking computation)
Algebra of types

82. List
(aggregates)
Disjunction
(error accumulation)
Kleisli
(dependency injection)
Future
(reactive non-blocking computation)
Algebra of types
Monad

83. List
(aggregates)
Disjunction
(error accumulation)
Kleisli
(dependency injection)
Future
(reactive non-blocking computation)
Algebra of types
Monad
Monoid

84. List
(aggregates)
Disjunction
(error accumulation)
Kleisli
(dependency injection)
Future
(reactive non-blocking computation)
Algebra of types
Monad
Monoid
Compositional

85. List
(aggregates)
Disjunction
(error accumulation)
Kleisli
(dependency injection)
Future
(reactive non-blocking computation)
Algebra of types
Monad
Monoid
Offers a suite of functional
combinators

86. List
(aggregates)
Disjunction
(error accumulation)
Kleisli
(dependency injection)
Future
(reactive non-blocking computation)
Algebra of types
Monad
Monoid
Handles edge cases so your domain
logic remains clean

87. List
(aggregates)
Disjunction
(error accumulation)
Kleisli
(dependency injection)
Future
(reactive non-blocking computation)
Algebra of types
Monad
Monoid
Implicitly encodes quite a bit of
domain rules

88. def clientOrders: Kleisli[List, ClientOrderSheet, Order]
def execute(m: Market, b: Account): Kleisli[List, Order, Execution]
def allocate(acts: List[Account]): Kleisli[List, Execution, Trade]
.. the algebra ..

89. def clientOrders: Kleisli[List, ClientOrderSheet, Order]
def execute(m: Market, b: Account): Kleisli[List, Order, Execution]
def allocate(acts: List[Account]): Kleisli[List, Execution, Trade]
.. the algebra ..
functions

90. .. the algebra ..
def clientOrders: Kleisli[List, ClientOrderSheet, Order]
def execute(m: Market, b: Account): Kleisli[List, Order, Execution]
def allocate(acts: List[Account]): Kleisli[List, Execution, Trade]
types

91. .. the algebra ..
composition
def tradeGeneration(market: Market, broker: Account,
clientAccounts: List[Account]) = {
clientOrders andThen
execute(market, broker) andThen
allocate(clientAccounts)
}

92. .. the algebra ..
trait OrderLaw {
def sizeLaw: Seq[ClientOrder] => Seq[Order] => Boolean =
{ cos => orders =>
cos.size == orders.size
}
def lineItemLaw: Seq[ClientOrder] => Seq[Order] => Boolean =
{ cos => orders =>
cos.map(instrumentsInClientOrder).sum ==
orders.map(_.items.size).sum
}
}
laws of the algebra
(domain rules)

93. Domain Rules as
Algebraic Properties
• part of the abstraction
• equally important as the actual
abstraction
• verifiable as properties

94. .. domain rules verification ..
property("Check Client Order laws") =
forAll((cos: Set[ClientOrder]) => {
val orders = for {
os <- clientOrders.run(cos.toList)
} yield os
sizeLaw(cos.toSeq)(orders) == true
lineItemLaw(cos.toSeq)(orders) == true
})
property based testing FTW ..

95. https://www.manning.com/books/functional-and-reactive-
domain-modeling

96. ThankYou!