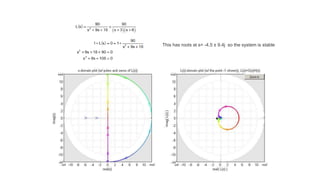
Frequency response plots show how a linear system responds to signals of different frequencies. They relate the input and output signals in the frequency domain. For continuous systems, the transfer function relates the Laplace transforms of the input and output. For discrete systems, it relates the Z-transforms. Frequency response plots provide insight into a system's frequency-dependent gains, resonances, and phase shifts. Common types of frequency response plots include Bode plots, which show magnitude and phase response on logarithmic frequency axes, and Nyquist plots, which show the transfer function in the complex plane. Stability can be assessed from these plots by examining properties like phase and gain margin.

1. What Is Frequency
Response?
Frequency response plots show the complex values of a transfer function as a
function of frequency.

2. • In the case of linear dynamic systems, the transfer function G is essentially an operator
that takes the input u of a linear system to the output y:
Y =Gu
For a continuous-time system, the transfer function relates the Laplace transforms of the
input U(s) and output Y(s):
Y(s) = G(s)U(s)
In this case, the frequency function G(iω) is the transfer function evaluated on the
imaginary axis s=iω.
For a discrete-time system sampled with a time interval T, the transfer function relates the
Z-transforms of the input U(z) and output Y(z) :
Y(z)=G(z)U(z)

3. Frequency response plots provide insight into linear
systems dynamics, such as frequency-dependent gains,
resonances, and phase shifts. Frequency response plots
also contain information about controller requirements and
achievable bandwidths

4. Options for Frequency-Response Plotting
The System Identification Toolbox provides three frequency-response plotting options.
Linear input-output models and frequency-response data models
Bode Plot
.
Nyquist Plot

5. Bode Plot
A Bode plot is a graph commonly used in control system engineering to determine the stability of a
control system. A Bode plot maps the frequency response of the system through two graphs – the
Bode magnitude plot (expressing the magnitude in decibels) and the Bode phase plot (expressing the
phase shift in degrees).
In both the plots, x-axis represents angular frequency (logarithmic scale). Whereas y axis represents
the magnitude (linear scale) of open loop transfer function in the magnitude plot and the phase angle
(linear scale) of the open loop transfer function in the phase plot.
M=20log|G(jω)H(jω)|
The magnitude of the open loop transfer function in dB is
The phase angle of the open loop transfer function in
degrees is
ϕ=∠G(jω)H(jω)

6. Basic of Bode Plots
The following table shows the slope, magnitude and the phase angle values of the
terms present in the open loop transfer function. This data is useful while drawing the
Bode plots.

7. Consider the open loop transfer function G(s)H(s)=K
Magnitude M= 20logK dB
Phase angle ϕ= 0 degrees
If K=1
, then magnitude is 0 dB.
If K>1
, then magnitude will be positive.
If K<1
, then magnitude will be negative.

8. The measured phase at 0 dB is -135°, so the phase
margin is 45°. The gain at -180° degrees is -9 dB, so the
gain margin is 9 dB. Since phase margin is positive, this
system is stable.
The measured gain is +13 dB when phase is -180°, so the
gain margin is -13 dB. At a gain of 0 dB, the measured
phase is minus 215°, so the phase margin is minus 35° at
the gain crossover point. This system is unstable.
Stable and unstable closed loop
systems

9. Nyquist Plot
is a parametric plot of a frequency response used in automatic control and signal processing. The most
common use of Nyquist plots is for assessing the stability of a system with feedback. In Cartesian coordinates,
the real part of the transfer function is plotted on the X-axis while the imaginary part is plotted on the Y-axis.

10. This has roots at s= -4.5 ± 9.4j so the system is stable

11. There are no poles of L(s) in the right half plane. This
means that the characteristic equation of the closed loop
transfer function has no zeros in the right half plane (the
closed loop transfer function has no poles there). The
system is stable.