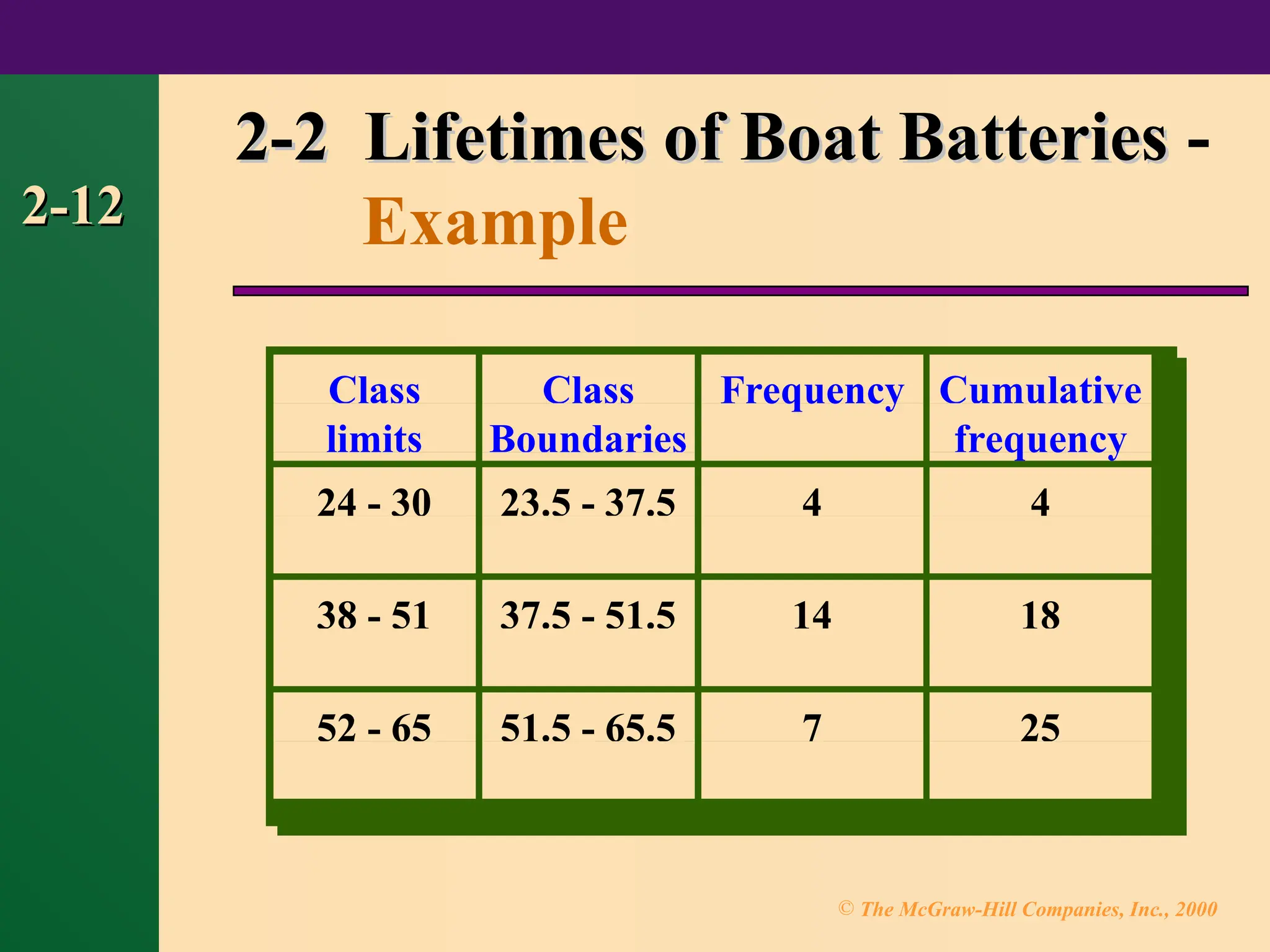
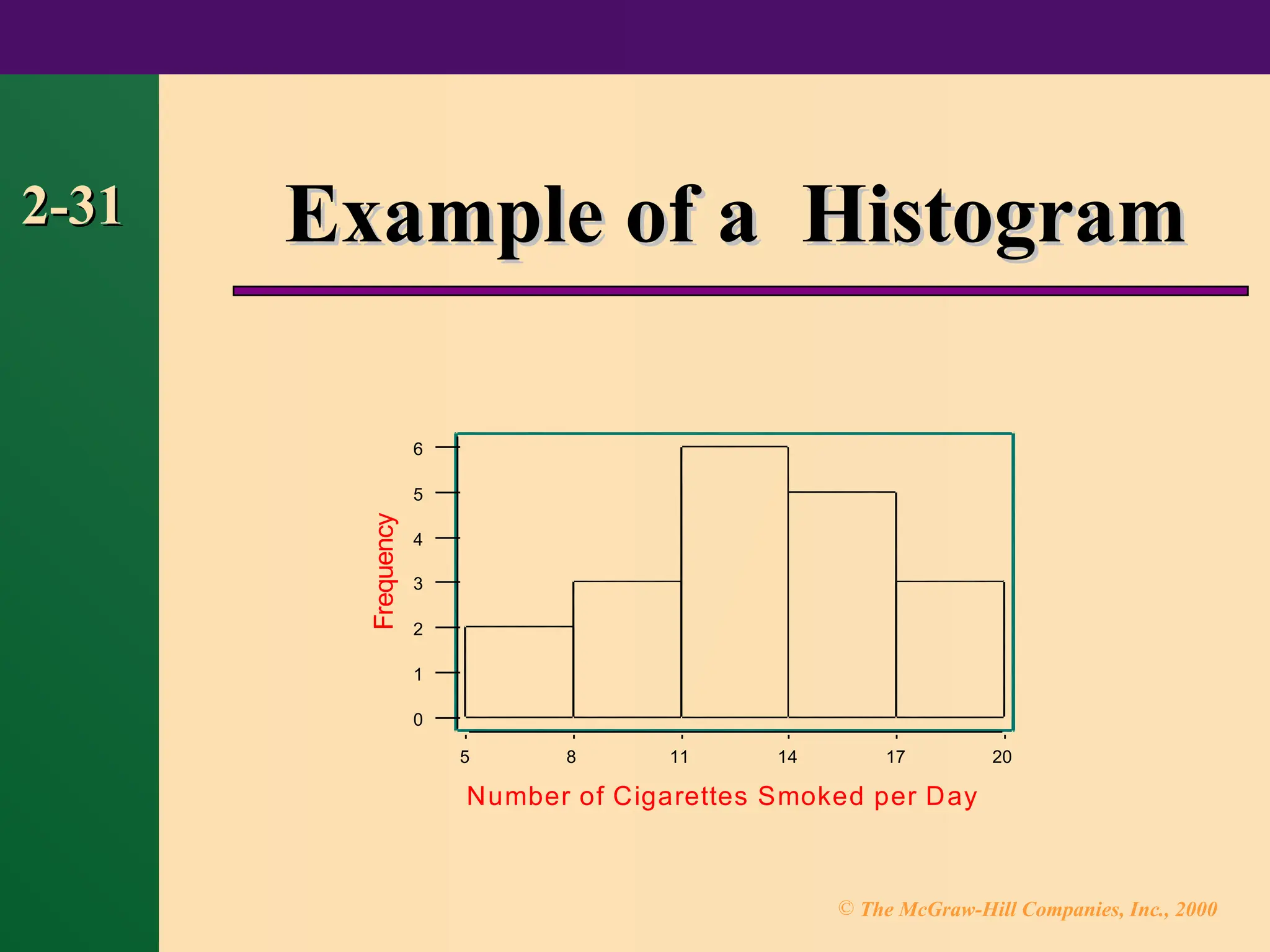
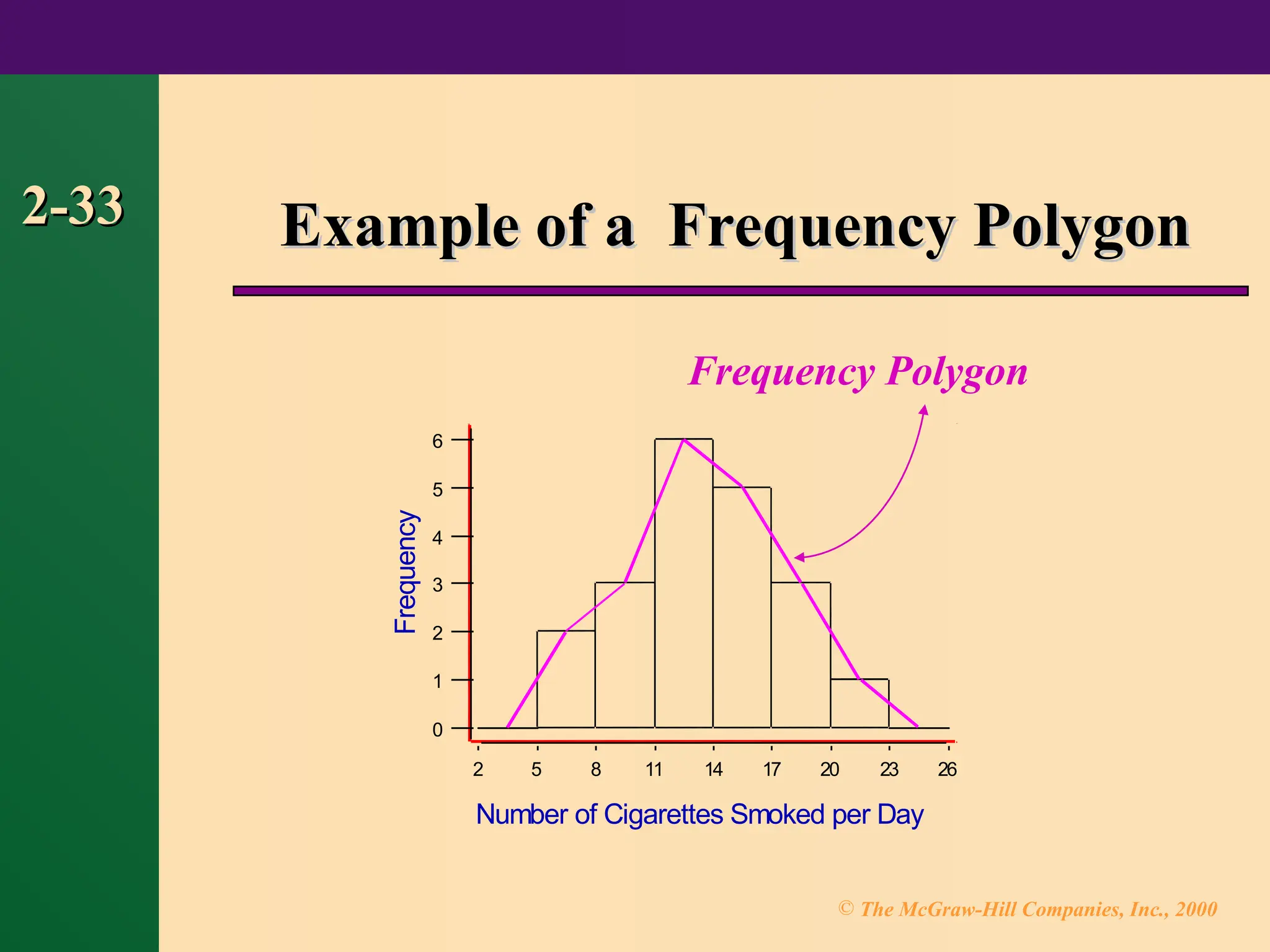
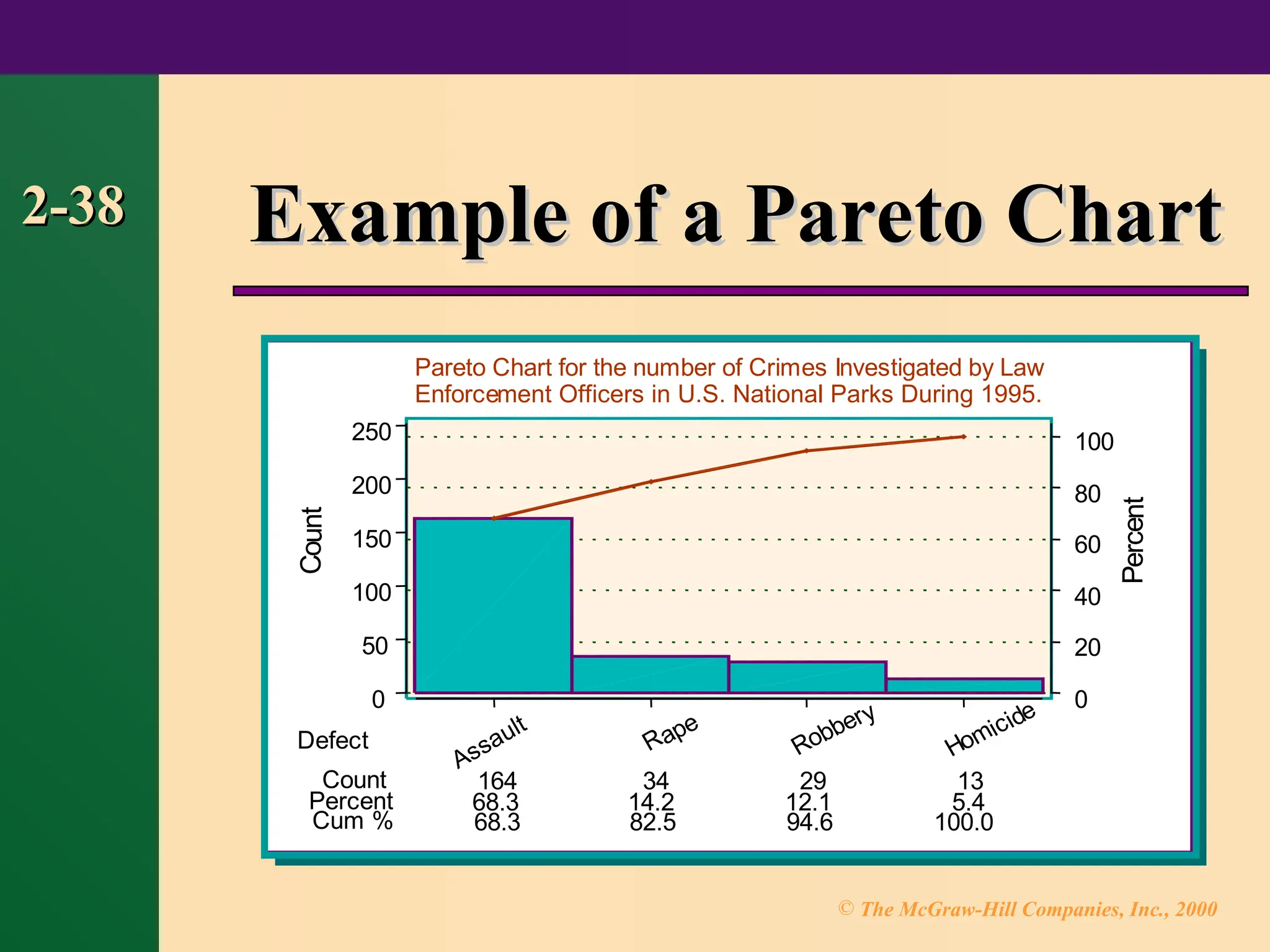
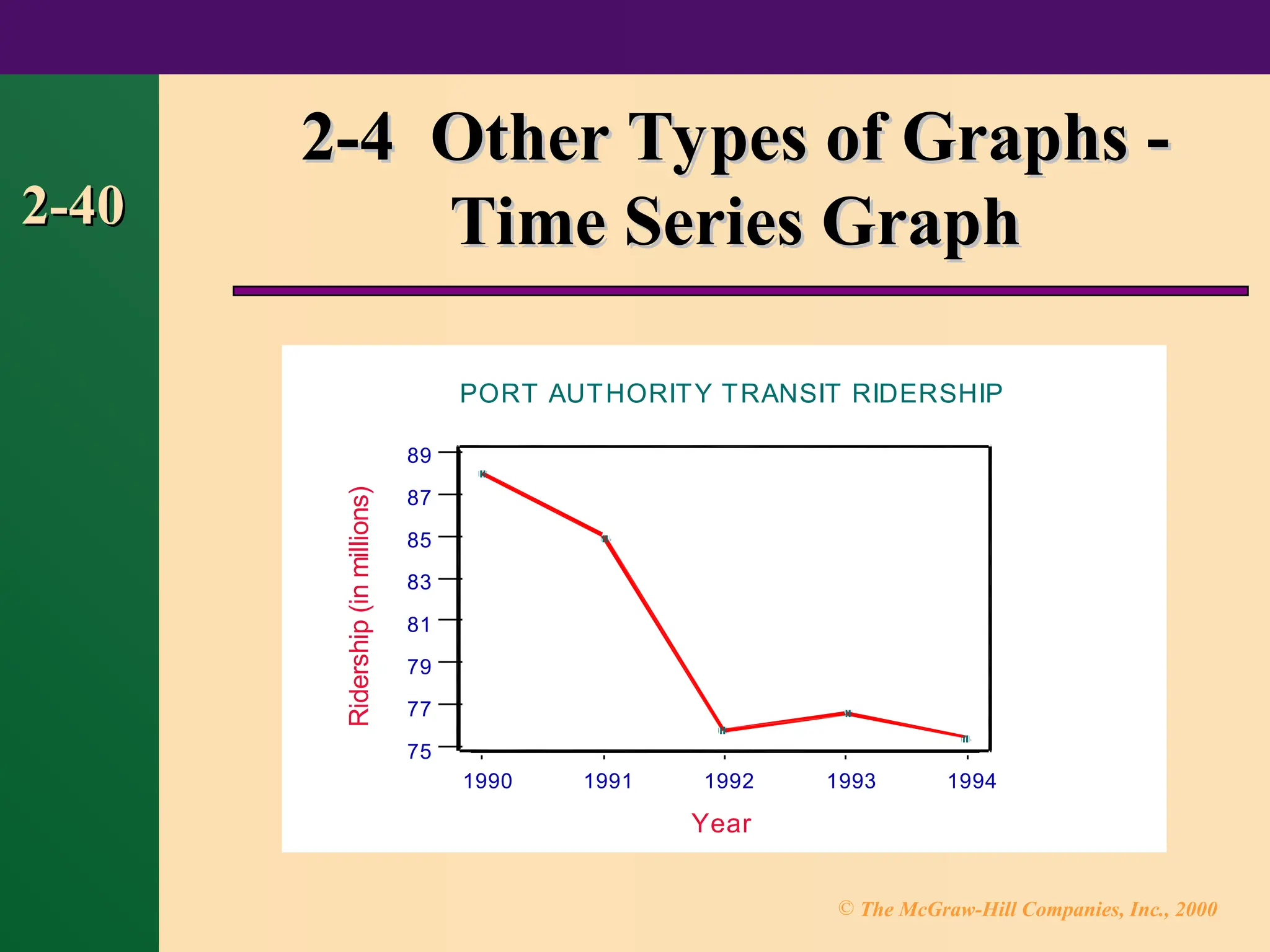
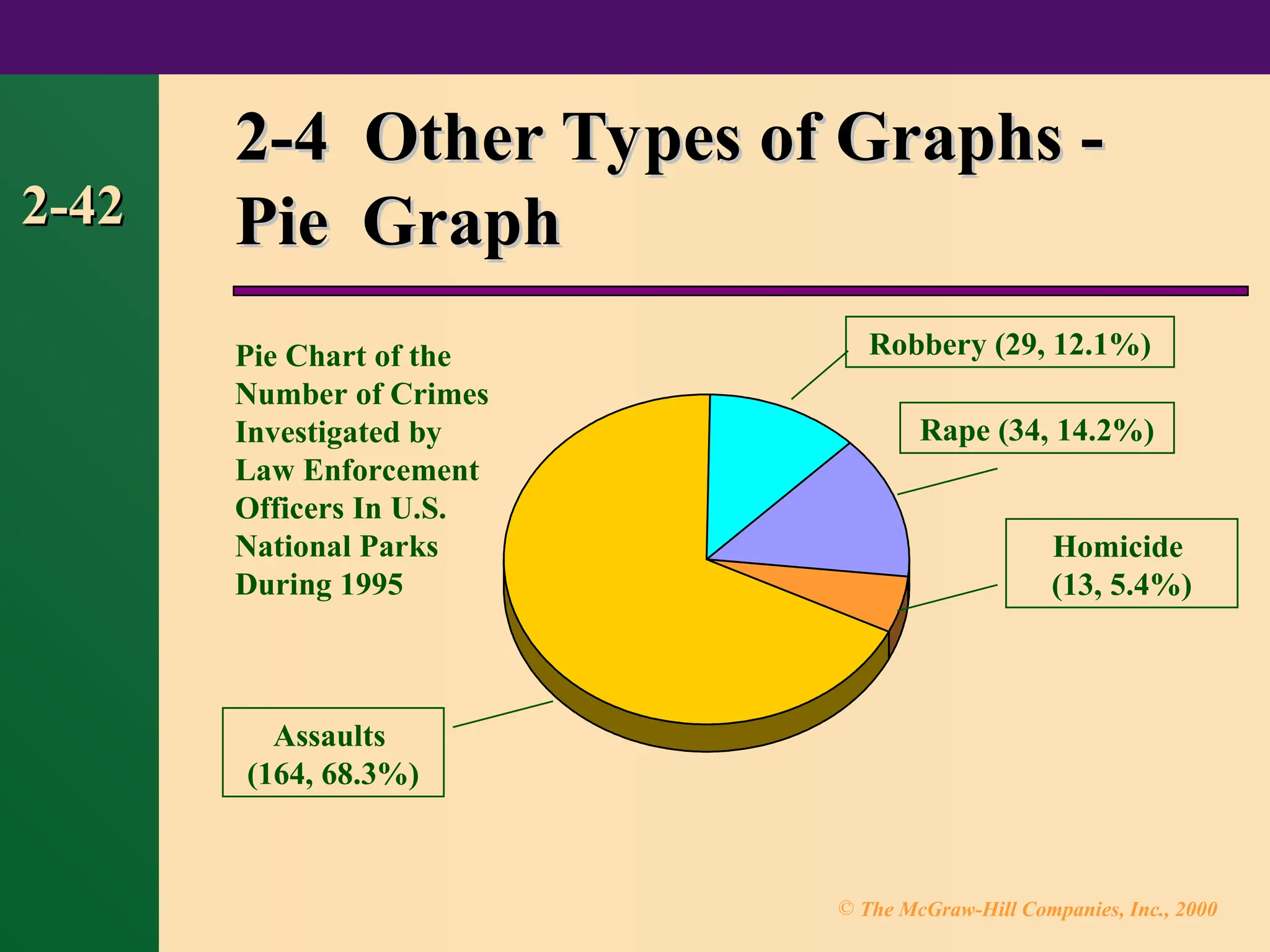
Chapter 2 focuses on frequency distributions and their graphical representations, including histograms, frequency polygons, and ogives. It outlines the organization of raw data into frequency distributions and discusses various types such as categorical, ungrouped, and grouped frequency distributions. The chapter also covers guidelines for constructing frequency distributions and introduces additional graph types like Pareto charts, time series graphs, and pie graphs.

1. © The McGraw-Hill Companies, Inc., 2000
2-1
2-1
Chapter 2
Chapter 2
Frequency Distributions
Frequency Distributions
and Graphs
and Graphs

2. © The McGraw-Hill Companies, Inc., 2000
2-2
2-2 Outline
Outline

2-1 Introduction

2-2 Organizing Data

2-3 Histograms, Frequency
Polygons, and Ogives

2-4 Other Types of Graphs

3. © The McGraw-Hill Companies, Inc., 2000
2-3
2-3 Objectives
Objectives

Organize data using frequency
distributions.

Represent data in frequency
distributions graphically using
histograms, frequency polygons,
and ogives.

4. © The McGraw-Hill Companies, Inc., 2000
2-4
2-4 Objectives
Objectives

Represent data using Pareto
charts, time series graphs, and
pie graphs.

5. © The McGraw-Hill Companies, Inc., 2000
2-5
2-5 2-2 Organizing Data
2-2 Organizing Data

When data are collected in original
form, they are called raw data
raw data.

When the raw data is organized
into a frequency distribution
frequency distribution, the
frequency
frequency will be the number of
values in a specific class of the
distribution.

6. © The McGraw-Hill Companies, Inc., 2000
2-6
2-6 2-2 Organizing Data
2-2 Organizing Data

A frequency distribution
frequency distribution is the
organizing of raw data in table
form, using classes and
frequencies.

The following slide shows an
example of a frequency
distribution.

7. © The McGraw-Hill Companies, Inc., 2000
2-7
2-7
2-2 Three Types of Frequency
2-2 Three Types of Frequency
Distributions
Distributions

Categorical frequency distributions
Categorical frequency distributions -
-
can be used for data that can be
placed in specific categories, such
as nominal- or ordinal-level data.

Examples -
Examples - political affiliation,
religious affiliation, blood type etc.

8. © The McGraw-Hill Companies, Inc., 2000
2-8
2-8
2-2 Blood Type Frequency
2-2 Blood Type Frequency
Distribution -
Distribution - Example
Class Frequency Percent
A 5 20
B 7 28
O 9 36
AB 4 16

9. © The McGraw-Hill Companies, Inc., 2000
2-9
2-9
2-2 Ungrouped Frequency
2-2 Ungrouped Frequency
Distributions
Distributions

Ungrouped frequency distributions -
Ungrouped frequency distributions -
can be used for data that can be
enumerated and when the range of
values in the data set is not large.

Examples -
Examples - number of miles your
instructors have to travel from home to
campus, number of girls in a 4-child
family etc.

10. © The McGraw-Hill Companies, Inc., 2000
2-10
2-10
2-2 Number of Miles Traveled
2-2 Number of Miles Traveled -
Example
Class Frequency
5 24
10 16
15 10

11. © The McGraw-Hill Companies, Inc., 2000
2-11
2-11
2-2 Grouped Frequency
2-2 Grouped Frequency
Distributions
Distributions

Grouped frequency distributions -
Grouped frequency distributions - can
be used when the range of values in the
data set is very large. The data must be
grouped into classes that are more than
one unit in width.

Examples -
Examples - the life of boat batteries in
hours.

12. © The McGraw-Hill Companies, Inc., 2000
2-12
2-12
2-2 Lifetimes of Boat Batteries
2-2 Lifetimes of Boat Batteries -
Example
Class
limits
Class
Boundaries
Cumulative
24 - 30 23.5 - 37.5 4 4
38 - 51 37.5 - 51.5 14 18
52 - 65 51.5 - 65.5 7 25
frequency
Frequency

13. © The McGraw-Hill Companies, Inc., 2000
2-13
2-13
2-2 Terms Associated with a
2-2 Terms Associated with a
Grouped Frequency Distribution
Grouped Frequency Distribution

Class limits represent the smallest and largest
data values that can be included in a class.

In the lifetimes of boat batteries example, the
values 24 and 30 of the first class are the class
class
limits
limits.

The lower class
lower class limit is 24 and the upper class
upper class
limit is 30.

14. © The McGraw-Hill Companies, Inc., 2000
2-14
2-14

The class boundaries
class boundaries are used to
separate the classes so that there
are no gaps in the frequency
distribution.
2-2 Terms Associated with a
2-2 Terms Associated with a
Grouped Frequency Distribution
Grouped Frequency Distribution

15. © The McGraw-Hill Companies, Inc., 2000
2-15
2-15

The class width
class width for a class in a
frequency distribution is found by
subtracting the lower (or upper)
class limit of one class minus the
lower (or upper) class limit of the
previous class.
2-2 Terms Associated with a
2-2 Terms Associated with a
Grouped Frequency Distribution
Grouped Frequency Distribution

16. © The McGraw-Hill Companies, Inc., 2000
2-16
2-16
2-2 Guidelines for Constructing
2-2 Guidelines for Constructing
a Frequency Distribution
a Frequency Distribution

There should be between 5 and 20
classes.

The class width should be an odd
number.

The classes must be mutually
exclusive.

17. © The McGraw-Hill Companies, Inc., 2000
2-17
2-17
2-2 Guidelines for Constructing
2-2 Guidelines for Constructing
a Frequency Distribution
a Frequency Distribution

The classes must be continuous.

The classes must be exhaustive.

The class must be equal in width.

18. © The McGraw-Hill Companies, Inc., 2000
2-18
2-18
2-2 Procedure for Constructing
2-2 Procedure for Constructing
a Grouped Frequency Distribution
a Grouped Frequency Distribution

Find the highest and lowest value.

Find the range.

Select the number of classes desired.

Find the width by dividing the range
by the number of classes and
rounding up.

19. © The McGraw-Hill Companies, Inc., 2000
2-19
2-19

Select a starting point (usually the
lowest value); add the width to get the
lower limits.

Find the upper class limits.

Find the boundaries.

Tally the data, find the frequencies, and
find the cumulative frequency.
2-2 Procedure for Constructing
2-2 Procedure for Constructing
a Grouped Frequency Distribution
a Grouped Frequency Distribution

20. © The McGraw-Hill Companies, Inc., 2000
2-20
2-20

In a survey of 20 patients who smoked,
the following data were obtained. Each
value represents the number of
cigarettes the patient smoked per day.
Construct a frequency distribution
using six classes. (The data is given on
the next slide.)
2-2 Grouped Frequency Distribution -
2-2 Grouped Frequency Distribution -
Example

21. © The McGraw-Hill Companies, Inc., 2000
2-21
2-21
10 8 6 14
22 13 17 19
11 9 18 14
13 12 15 15
5 11 16 11
2-2 Grouped Frequency Distribution -
2-2 Grouped Frequency Distribution -
Example

22. © The McGraw-Hill Companies, Inc., 2000
2-22
2-22

Step 1:
Step 1: Find the highest and lowest
values: H = 22 and L = 5.

Step 2:
Step 2: Find the range:
R = H – L = 22 – 5 = 17.

Step 3:
Step 3: Select the number of classes
desired. In this case it is equal to 6.
2-2 Grouped Frequency Distribution -
2-2 Grouped Frequency Distribution -
Example

23. © The McGraw-Hill Companies, Inc., 2000
2-23
2-23

Step 4:
Step 4: Find the class width by
dividing the range by the number
of classes. Width = 17/6 = 2.83.
This value is rounded up to 3.
2-2 Grouped Frequency Distribution -
2-2 Grouped Frequency Distribution -
Example

24. © The McGraw-Hill Companies, Inc., 2000
2-24
2-24

Step 5:
Step 5: Select a starting point for
the lowest class limit. For
convenience, this value is chosen
to be 5, the smallest data value.
The lower class limits will be 5, 8,
11, 14, 17, and 20.
2-2 Grouped Frequency Distribution -
2-2 Grouped Frequency Distribution -
Example

25. © The McGraw-Hill Companies, Inc., 2000
2-25
2-25

Step 6:
Step 6: The upper class limits will
be 7, 10, 13, 16, 19, and 22. For
example, the upper limit for the
first class is computed as 8 - 1, etc.
2-2 Grouped Frequency Distribution -
2-2 Grouped Frequency Distribution -
Example

26. © The McGraw-Hill Companies, Inc., 2000
2-26
2-26

Step 7:
Step 7: Find the class boundaries
by subtracting 0.5 from each lower
class limit and adding 0.5 to the
upper class limit.
2-2 Grouped Frequency Distribution -
2-2 Grouped Frequency Distribution -
Example

27. © The McGraw-Hill Companies, Inc., 2000
2-27
2-27

Step 8:
Step 8: Tally the data, write the
numerical values for the tallies in the
frequency column, and find the
cumulative frequencies.

The grouped frequency distribution
is shown on the next slide.
2-2 Grouped Frequency Distribution -
2-2 Grouped Frequency Distribution -
Example

28. © The McGraw-Hill Companies, Inc., 2000
2-28
2-28
Class Limits Class Boundaries Frequency Cumulative Frequency
05 to 07 4.5 - 7.5 2 2
08 to 10 7.5 - 10.5 3 5
11 to 13 10.5 - 13.5 6 11
14 to 16 13.5 - 16.5 5 16
17 to 19 16.5 - 19.5 3 19
20 to 22 19.5 - 22.5 1 20
Note: The dash “-” represents “to”.

29. © The McGraw-Hill Companies, Inc., 2000
2-29
2-29
2-3 Histograms, Frequency
2-3 Histograms, Frequency
Polygons, and Ogives
Polygons, and Ogives

The three most commonly used
The three most commonly used
graphs in research are:
graphs in research are:

The histogram.

The frequency polygon.

The cumulative frequency graph,
or ogive (pronounced o-jive).

30. © The McGraw-Hill Companies, Inc., 2000
2-30
2-30

The histogram
histogram is a graph that
displays the data by using vertical
bars of various heights to
represent the frequencies.
2-3 Histograms, Frequency
2-3 Histograms, Frequency
Polygons, and Ogives
Polygons, and Ogives

31. © The McGraw-Hill Companies, Inc., 2000
2-31
2-31 Example of a Histogram
Example of a Histogram
20
17
14
11
8
5
6
5
4
3
2
1
0
Number of Cigarettes Smoked per Day
Frequency

32. © The McGraw-Hill Companies, Inc., 2000
2-32
2-32

A frequency polygon
frequency polygon is a graph
that displays the data by using
lines that connect points plotted
for frequencies at the midpoint of
classes. The frequencies
represent the heights of the
midpoints.
2-3 Histograms, Frequency
2-3 Histograms, Frequency
Polygons, and Ogives
Polygons, and Ogives

33. © The McGraw-Hill Companies, Inc., 2000
2-33
2-33 Example of a Frequency Polygon
Example of a Frequency Polygon
Frequency Polygon
26
23
20
17
14
11
8
5
2
6
5
4
3
2
1
0
Number of Cigarettes Smoked per Day
Frequency

34. © The McGraw-Hill Companies, Inc., 2000
2-34
2-34

A cumulative frequency graph
cumulative frequency graph or
ogive
ogive is a graph that represents the
cumulative frequencies for the
classes in a frequency distribution.
2-3 Histograms, Frequency
2-3 Histograms, Frequency
Polygons, and Ogives
Polygons, and Ogives

35. © The McGraw-Hill Companies, Inc., 2000
2-35
2-35 Example of an Ogive
Example of an Ogive
26
23
20
17
14
11
8
5
2
20
10
0
Number of Cigarettes Smoked per Day
Cumulative
Frequency Ogive

36. © The McGraw-Hill Companies, Inc., 2000
2-36
2-36 2-4 Other Types of Graphs
2-4 Other Types of Graphs

Pareto charts -
Pareto charts - a Pareto chart is
used to represent a frequency
distribution for a categorical
variable.

37. © The McGraw-Hill Companies, Inc., 2000
2-37
2-37
2-4 Other Types of Graphs-Pareto
2-4 Other Types of Graphs-Pareto
Chart
Chart

When constructing a Pareto chart -

Make the bars the same width.

Arrange the data from largest to
smallest according to frequencies.

Make the units that are used for the
frequency equal in size.

38. © The McGraw-Hill Companies, Inc., 2000
2-38
2-38 Example of a Pareto Chart
Example of a Pareto Chart
Homicide
Robbery
Rape
Assault
13
29
34
164
5.4
12.1
14.2
68.3
100.0
94.6
82.5
68.3
250
200
150
100
50
0
100
80
60
40
20
0
Defect
Count
Percent
Cum %
Perce
nt
Co
unt
Enforcement Officers in U.S. National Parks During 1995.
Pareto Chart for the number of Crimes Investigated by Law

39. © The McGraw-Hill Companies, Inc., 2000
2-39
2-39 2-4 Other Types of Graphs
2-4 Other Types of Graphs

Time series graph -
Time series graph - A time series
graph represents data that occur
over a specific period of time.

40. © The McGraw-Hill Companies, Inc., 2000
2-40
2-40
2-4 Other Types of Graphs -
2-4 Other Types of Graphs -
Time Series Graph
Time Series Graph
1994
1993
1992
1991
1990
89
87
85
83
81
79
77
75
Year
Ridership
(in
millions)
PORT AUTHORITY TRANSIT RIDERSHIP

41. © The McGraw-Hill Companies, Inc., 2000
2-41
2-41 2-4 Other Types of Graphs
2-4 Other Types of Graphs

Pie graph -
Pie graph - A pie graph is a circle
that is divided into sections or
wedges according to the
percentage of frequencies in each
category of the distribution.

42. © The McGraw-Hill Companies, Inc., 2000
2-42
2-42
2-4 Other Types of Graphs -
2-4 Other Types of Graphs -
Pie
Pie Graph
Graph
Robbery (29, 12.1%)
Rape (34, 14.2%)
Assaults
(164, 68.3%)
Homicide
(13, 5.4%)
Pie Chart of the
Number of Crimes
Investigated by
Law Enforcement
Officers In U.S.
National Parks
During 1995