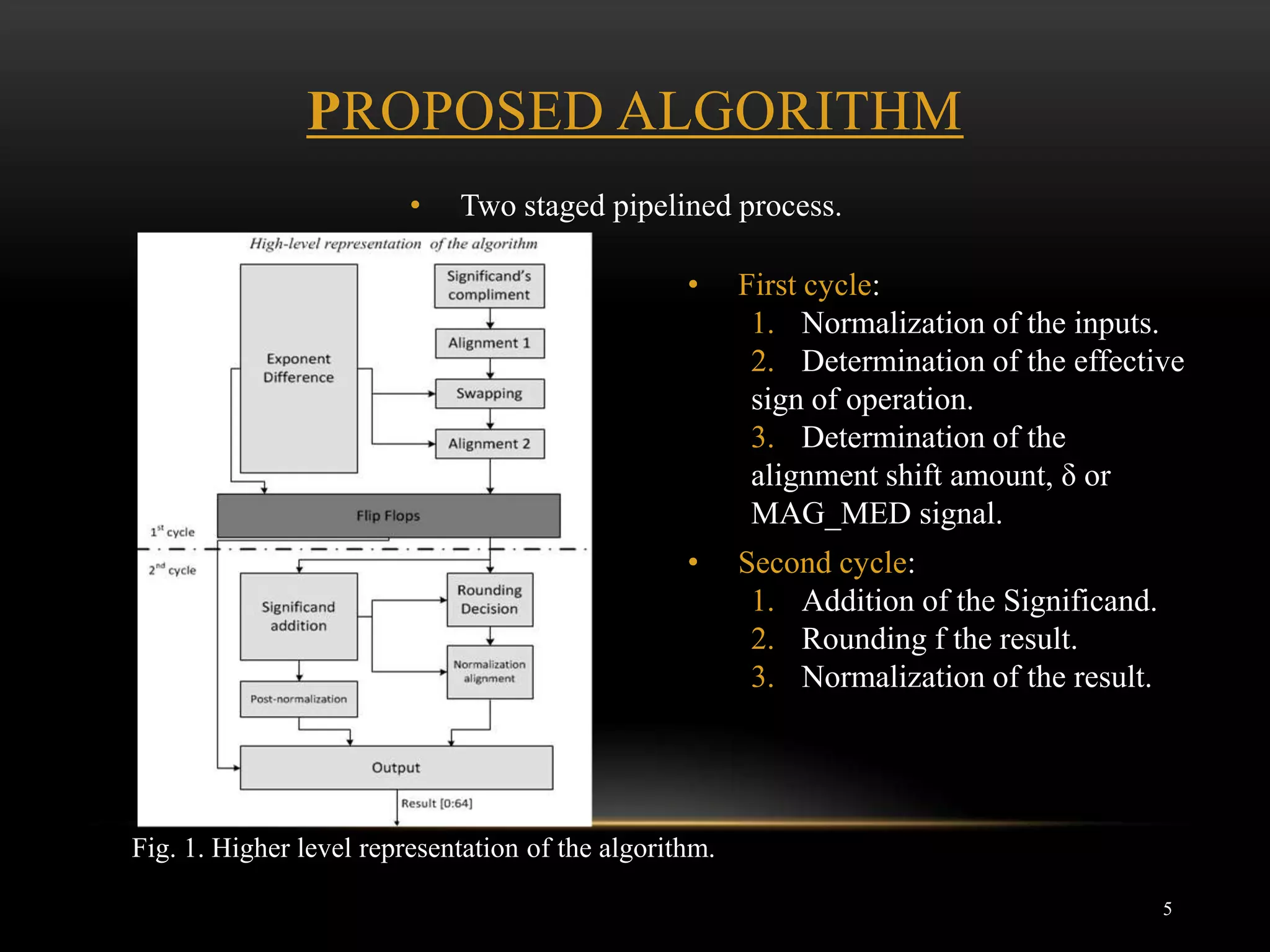
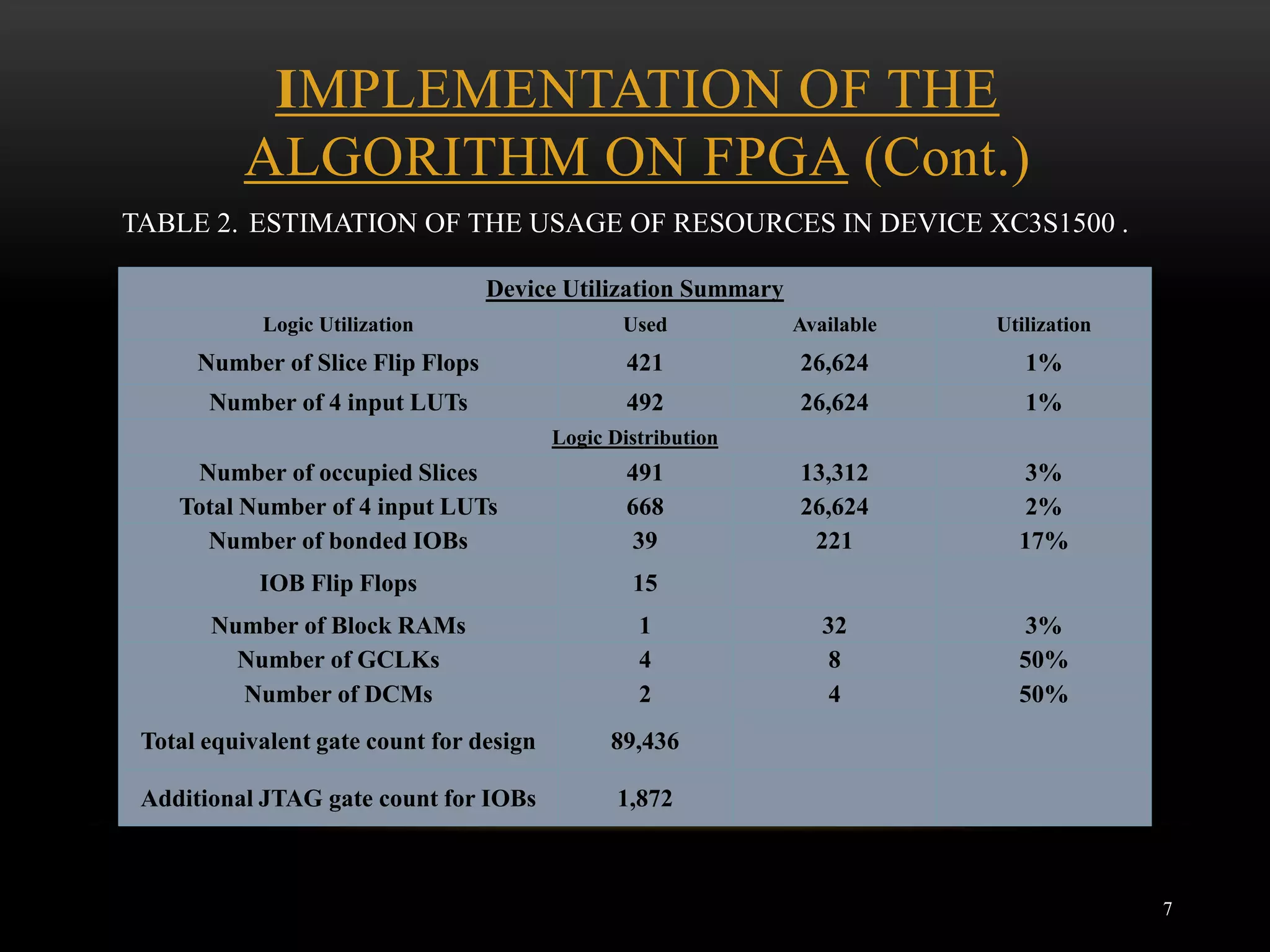
This document describes an FPGA implementation of a double precision IEEE floating point adder. It outlines the general structure of IEEE 754 double precision numbers, describes the simple arithmetic operation of adding two such numbers, and proposes a two stage pipelined algorithm to perform the addition. It then discusses implementing the algorithm on FPGA devices, providing resource usage estimates and illustrations of the first two cycles of the algorithm. Simulation results are presented and the conclusions discuss the benefits of this technique for performing floating point additions with low latency.

1. FPGA BASED IMPLEMENTATION OF A
DOUBLE PRECISION IEEE FLOATING-
POINT ADDER
Presented By
Somsubhra Ghosh
Dept. of Electrical Engineering
JADAVPUR UNIVERSITY
Kolkata - 700032
1

2. OUTLINE
 General Structure.
 Simple arithmetic operation of the double precision
floating-point numbers.
 Proposed algorithm .
 Implementation of the algorithm on FPGA.
 Detailed illustration of the first cycle of the algorithm.
 Discussions and simulation results.
 Conclusions.
 References.
2

3. GENERAL STRUCTURE
General representation of IEEE 754-2008 double precision floating-point
numbers.
0 1-11 12-64
(length = 1) (length = 11) (length = 52)
Sign(S) Exponent(E) Significand(F)
3

4. SIMPLE ARITHMETIC OPERATION OF THE
DOUBLE PRECISION FLOATING-POINT
NUMBERS
• The required operation is performed by the following formula:
rnd (sum) rnd (( 1)sa 2ea fa ( 1)( SOP sb )
2eb fb)
where
S.EFF sa sb SOP
So,
sum ( 1)sl 2el ( fl ( 1)S .EFF ( fs 2 | ))
4

5. PROPOSED ALGORITHM
• Two staged pipelined process.
• First cycle:
1. Normalization of the inputs.
2. Determination of the effective
sign of operation.
3. Determination of the
alignment shift amount, δ or
MAG_MED signal.
• Second cycle:
1. Addition of the Significand.
2. Rounding f the result.
3. Normalization of the result.
Fig. 1. Higher level representation of the algorithm.
5

6. IMPLEMENTATION OF THE
ALGORITHM ON FPGA
• The implementation off the presented algorithm has been performed using two
different Xilinx © products, XC2V6000 device of virtex2 family and XC3S1500 of
spartan-3 family.
TABLE 1. ESTIMATION OF THE USAGE OF RESOURCES IN DEVICE XC2V6000.
Device Utilization Summary
Logic Utilization Used Available Utilization
Number of Slice Flip Flops 308 67,584 0%
Number of 4 input LUTs 932 67,584 1%
Logic Distribution
Number of occupied Slices 546 33,792 1%
Total Number of 4 input
932 67,584 1%
LUTs
Number of bonded IOBs 195 824 23%
Number of GCLKs 2 16 12%
6

7. IMPLEMENTATION OF THE
ALGORITHM ON FPGA (Cont.)
TABLE 2. ESTIMATION OF THE USAGE OF RESOURCES IN DEVICE XC3S1500 .
Device Utilization Summary
Logic Utilization Used Available Utilization
Number of Slice Flip Flops 421 26,624 1%
Number of 4 input LUTs 492 26,624 1%
Logic Distribution
Number of occupied Slices 491 13,312 3%
Total Number of 4 input LUTs 668 26,624 2%
Number of bonded IOBs 39 221 17%
IOB Flip Flops 15
Number of Block RAMs 1 32 3%
Number of GCLKs 4 8 50%
Number of DCMs 2 4 50%
Total equivalent gate count for design 89,436
Additional JTAG gate count for IOBs 1,872
7

8. DETAILED ILLUSTRATION OF THE
FIRST CYCLE OF THE ALGORITHM
FB[0:52]
FA[0:52]
SA
SOP
SB
EA EB
FLIP FLOPS ONE’S COMPLEMENT S.EFF
FAO[0:52] FBO[0:52]
ADDER (5) ADDER (7)
PRESHIFT
SIGN_MED 1 0
XOR FSOP[-1:53] MUX
XOR
0 1
MUX
MAG_MED[5:0] SHIFT(63)
ORTREE SHIFT(65)
FL[0:52]
0 1
IS_BIG MUX SHIFT(1)
FSOPA[-1:116] FLP[-1:52]
SIGN_BIG
Fig. 2. Block level representation of the 1st cycle of the algorithm.
8

9. DETAILED ILLUSTRATION OF THE
FIRST CYCLE OF THE ALGORITHM
(CONT.)
Fig. 3. Block level representation of the 2nd cycle of the algorithm.
9

10. DISCUSSIONS AND SIMULATION
RESULTS
Fig. 4. Simulation of the floating point adder at Xilinx© ISE using the: (a) Behavioral
simulation, (b) Post-route and synthesis simulation, (c) Technical schematic.
10

11. CONCLUSIONS
 The system has a minimum period of 14.081ns or a maximum frequency
of 71.017MHz.
 This technique successfully demonstrates a very low latency and a scope
of achieving an even lower latencies with the use of intricate and more
complex computational techniques.
 This technique shows significant improvements over the present way of
performing he arithmetic operations of the floating-point numbers in
terms of latency, ease, flexibility, and robustness against errors.
 This implementation offers a faster and smarter estimation of the results
with minimal errors and ensures minimal computational load for the
system.

12. REFERENCES
 Peter-Michael Seidel, Guy Even, “Delay-Optimized Implementation of IEEE
Floating-Point Addition”, IEEE Trans. on Computers, vol. 53, no. 2, pp. 97-
113, Feb. 2004.
 Karan Gumber, Sharmelee Thangjam, “Performance Analysis of Floating Point
Adder using VHDL on Reconfigurable Hardware”, International Journal of
Computer Applications, vol. 46, no. 9, pp. 1-5, May 2012.
 N. Kikkeri, P.M. Seidel, “An FPGA Implementation of a Fully Verified Double
Precision IEEE Floating-Point Adder”, Proc. of IEEE International Conference
on Application-specific Systems, Architectures and Processors, pp. 83-88, 9-11
July 2007.
 A. Tyagi, “A Reduced-Area Scheme for Carry-Select Adders”, IEEE trans. on
Computers, vol. 42, no. 10, pp. 1163-1170, Oct. 1993.
 A. Beaumont-Smith, N. Burgess, S. Lefrere, C. Lim, “Reduced Latency IEEE
Floating-Point Standard Adder Architectures,” Proc. of 14th IEEE Symposium
on Computer Arithmetic, pp. 35-43, 1999.
12

13. REFERENCES (Cont.)
 P. Farmwald, “On the Design of High Performance Digital Arithmetic Units,”
PhD thesis, Stanford Univ., Aug. 1981.
 A. Nielsen, D. Matula, C. N. Lyu, G. Even, “IEEE Compliant Floating-Point
Adder that Conforms with the Pipelined Packet-Forwarding Paradigm,” IEEE
Trans. on Computers, vol. 49, no. 1, pp. 33-47, Jan. 2000.
 N. Quach, N. Takagi, and M. Flynn, “On fast IEEE Rounding”, Technical
Report CSL-TR-91-459, Stanford Univ., Jan. 1991.
 P.-M. Seidel, “On The Design of IEEE Compliant Floating-Point Units and
Their Quantitative Analysis”, PhD thesis, Univ. of Saarland, Germany, Dec.
1999.
 P.-M. Seidel, G. Even, “How Many Logic Levels Does Floating-Point
Addition Require?”, Proc. of International Conference on Computer Design
(ICCD ’98): VLSI, in Computers & Processors, pp. 142-149, Oct. 1998.
 W.C. Park, T.D. Han, S.D. Kim, S.B. Yang, “Floating Point Adder/Subtractor
Performing IEEE Rounding and Addition/Subtraction in Parallel”, IEICE
Trans. on Information and Systems, vol. 4, pp. 297-305, 1996.
13

14. REFERENCES (Cont.)
 S. Oberman, H. Al-Twaijry, and M. Flynn, “The SNAP Project: Design of
Floating Point Arithmetic Units”, Proc. of 13th IEEE Symposium on
Computer Arithmetic, pp. 156-165, 1997.
 S. Oberman, “Floating-Point Arithmetic Unit Including an Efficient Close
Data Path,” AMD, US patent 6094668, 2000.
 V. Gorshtein, A. Grushin, and S. Shevtsov, “Floating Point Addition Methods
and Apparatus.” Sun Microsystems, US patent 5808926, 1998.
 G. Even, P.M. Seidel, “A comparison of three rounding algorithms for IEEE
floating-point multiplication”, Proc. of 14th IEEE Symposium on Computer
Arithmetic, pp. 225-232, 1999.
 IEEE Computer Society, “IEEE Standard for Floating-Point Arithmetic”,
IEEE Std. 754 TM-2008 (Revision of IEEE Std 754-1985), Aug. 29, 2008.
 H. D. Nguyen, B. Pasca, T. B. Preuber, “FPGA-Specific Arithmetic
Optimizations of Short-Latency Adders,” Proc. of 21 st IEEE international
conference on field programmable logic and applications, pp. 232 – 237,
2011.
14

15. REFERENCES (Cont.)
 C. Minchola, M. Vazquez, G. Sutter, “A FPGA IEEE-754-2008 DECIMAL64
FLOATING-POINT ADDER/SUBTRACTOR,” Proc. of VII Southern
conference on Programmable Logic, pp. 251 – 256, 2011.
 F. Dinechin, H. D. Nguyen, B. Pasca, “Pipelined FPGA Adders,” Proc. of
International conference on Field Programmable Logic and applications, pp.
422 – 427, 2010.
15

16. QUESTIONS?
Polygonia interrogationis known as Question Mark

17. Thank You
17