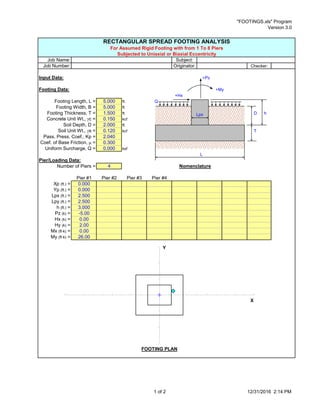
This document describes a spreadsheet program that analyzes rectangular spread footings subjected to uniaxial or biaxial eccentric loading from 1 to 8 piers. It provides input fields for footing geometry, material properties, pier locations and loads. The program then calculates the total load and eccentricities, checks for overturning, sliding and uplift, determines the bearing length and pressure distribution, and reports the maximum net soil pressure.

1. "FOOTINGS.xls" Program
Version 3.0
RECTANGULAR SPREAD FOOTING ANALYSIS
For Assumed Rigid Footing with from 1 To 8 Piers
Subjected to Uniaxial or Biaxial Eccentricity
Job Name: Subject:
Job Number: Originator: Checker:
Input Data: +Pz
Footing Data: +My
+Hx
Footing Length, L = 5.000 ft. Q
Footing Width, B = 5.000 ft.
Footing Thickness, T = 1.500 ft. D h
Concrete Unit Wt., gc = 0.150 kcf
Soil Depth, D = 2.000 ft.
Soil Unit Wt., gs = 0.120 kcf T
Pass. Press. Coef., Kp = 2.040
Coef. of Base Friction, m = 0.300
Uniform Surcharge, Q = 0.000 ksf
L
Pier/Loading Data:
Number of Piers = 4 Nomenclature
Pier #1 Pier #2 Pier #3 Pier #4
Xp (ft.) = 0.000
Yp (ft.) = 0.000
Lpx (ft.) = 2.500
Lpy (ft.) = 2.500
h (ft.) = 3.000
Pz (k) = -5.00
Hx (k) = 0.00
Hy (k) = 2.00
Mx (ft-k) = 0.00
My (ft-k) = 26.00
FOOTING PLAN
Y
X
Lpx
1 of 2 12/31/2016 2:14 PM

2. "FOOTINGS.xls" Program
Version 3.0
Results: Nomenclature for Biaxial Eccentricity:
Case 1: For 3 Corners in Bearing
Total Resultant Load and Eccentricities: (Dist. x > L and Dist. y > B)
SPz = -17.94 kips Dist. x
ex = 1.45 ft. (> L/6) Pmax
ey = 0.50 ft. (<= B/6)
Overturning Check:
SMrx = 44.84 ft-kips
SMox = -9.00 ft-kips Dist. y
FS(ot)x = 4.983 (>= 1.5)
SMry = 44.84 ft-kips
SMoy = 26.00 ft-kips
FS(ot)y = 1.725 (>= 1.5)
Case 2: For 2 Corners in Bearing
Sliding Check: (Dist. x > L and Dist. y <= B)
Pass(x) = 5.05 kips Dist. x
Frict(x) = 5.38 kips Pmax
FS(slid)x = N.A.
Passive(y) = 5.05 kips
Frict(y) = 5.38 kips Dist. y
FS(slid)y = 5.215 (>= 1.5) Brg. Ly2
Uplift Check:
SPz(down) = -17.94 kips
SPz(uplift) = 0.00 kips
FS(uplift) = N.A.
Case 3: For 2 Corners in Bearing
Bearing Length and % Bearing Area: (Dist. x <= L and Dist. y > B)
Dist. x = 3.885 ft. Dist. x
Dist. y = 10.575 ft. Brg. Lx2 Pmax
Brg. Lx1 = 2.048 ft.
Brg. Lx2 = 3.885 ft.
%Brg. Area = 59.33 %
Biaxial Case = Case 3 6*ex/L + 6*ey/B = 2.34
Dist. y
Gross Soil Bearing Corner Pressures:
P1 = 1.618 ksf
P2 = 3.070 ksf
P3 = 0.000 ksf
P4 = 0.000 ksf Case 4: For 1 Corner in Bearing
(Dist. x <= L and Dist. y <= B)
Dist. x
P3=0 ksf P2=3.07 ksf Brg. Lx Pmax
B
P4=0 ksf L P1=1.618 ksf Dist. y
CORNER PRESSURES Brg. Ly
Maximum Net Soil Pressure:
Pmax(net) = Pmax(gross)-(D+T)*gs
Pmax(net) = 2.650 ksf
Brg. Ly
Line of zero
pressure Brg. Lx
Line of zero
pressure Brg. Lx1
Line of zero pressure
Brg. Ly1
Line of zero
pressure
2 of 2 12/31/2016 2:14 PM