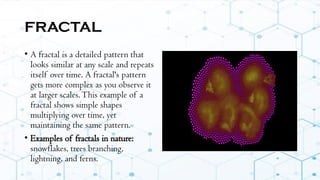
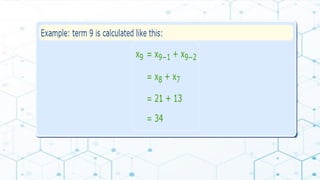
The document discusses mathematical patterns found in nature, including fractals, spirals, and Voronoi patterns, each characterized by unique repetitive structures that can be observed at different scales. It highlights examples of these patterns, such as snowflakes and hurricanes, and introduces the Fibonacci sequence, explaining its historical significance and its role in modeling natural growth patterns. The Fibonacci sequence is defined mathematically, showcasing how it can generate complex spirals through a simple iterative rule.

1. MATHEMATICS IN THE
MODERN WORLD
MODULE #2
RECOGNIZING PATTERNS IN NATURE AND
CONFIGURATIONS IN THE WORLD

2. MATH PATTERNS IN NATURE
*FRACTAL
*SPIRAL
*VORONOI

3. FRACTAL
• A fractal is a detailed pattern that
looks similar at any scale and repeats
itself over time. A fractal's pattern
gets more complex as you observe it
at larger scales.This example of a
fractal shows simple shapes
multiplying over time, yet
maintaining the same pattern.
• Examples of fractals in nature:
snowflakes, trees branching,
lightning, and ferns.

4. SPIRAL
• A spiral is a curved pattern that
focuses on a center point and a
series of circular shapes that
revolve around it.
• Examples of spirals are pine
cones, pineapples, hurricanes.

5. VORONOI
• AVoronoi pattern provides clues to
nature’s tendency to favor efficiency:
the nearest neighbor, shortest path,
and tightest fit. Each cell in a
Voronoi pattern has a seed point.
• Examples of Voronoi patterns are
the skin of a giraffe, corn on the
cob, honeycombs, foam bubbles, the
cells in a leaf, and a head of garlic.

6. PATTERNS:
Watch:
https://vimeo.com/9953368

7. FIBONACCI SEQUENCE

8. FIBONACCI SEQUENCE
The Fibonacci sequence named after the
Italian mathematician Leonardo Fibonacci
of PIsa. His real name was Leonardo
Pisano Bogollo, and he lived between 1170
and 1250 in Italy.
"Fibonacci" was his nickname, which
roughly means "Son of Bonacci", who in
1202 introduced the sequence. It turns out
that simple equations involving the
Fibonacci numbers can describe most of
the complex spiral growth patterns found
in nature.

9. RULE OF FIBONACCI SEQUENCE
The Fibonacci Sequence can be written as a "Rule". First, the terms are
numbered from 0 onwards like this:
So term number 6 is called
x6 (which equals 8).

10. RULE OF FIBONACCI SEQUENCE
So we can write the rule:
The Rule is xn = xn 1 + x
− n 2
−
where:
xn is term number "n"
xn 1
− is the previous term (n 1)
−
xn 2
− is the term before that (n 2)
−

12. MAKE A SPIRAL
When we make squares with those widths, we get a nice spiral:
Do you see how the squares fit neatly together?
For example 5 and 8 make 13, 8 and 13 make 21, and so on.

13. REFERENCES:
• https://www.fi.edu/math-patterns-nature
• https://www.mathsisfun.com/numbers/fibonacci-sequence.html