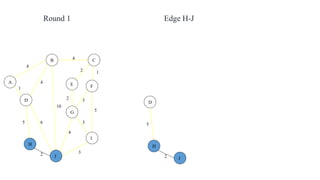
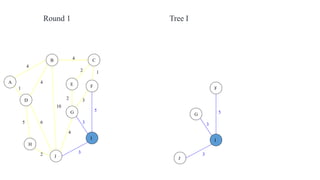
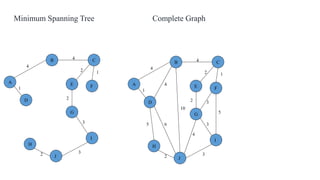
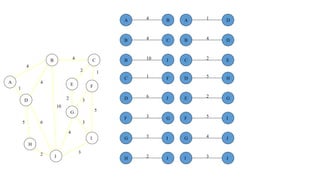
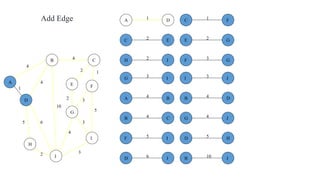
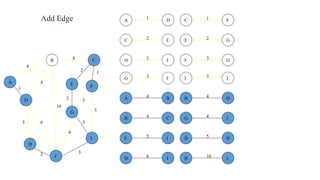
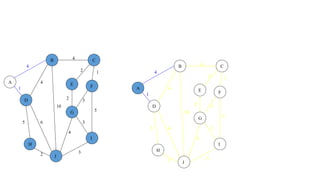
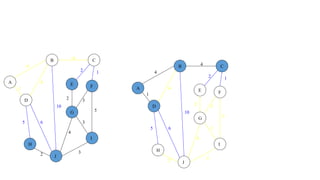
The document discusses algorithms for finding minimum spanning trees in graphs. It explains that a spanning tree is a subgraph that connects all vertices using the minimum total edge weight. Kruskal's and Prim's algorithms are described for finding the minimum spanning tree by sequentially adding edges that do not form cycles. Pseudocode and time complexity analysis are provided for both algorithms, with Prim's and Kruskal's algorithms having time complexities of O(E log V) and O(E log E), respectively, where V is the number of vertices and E is the number of edges.

1. By
Mohammad Shahriar Reza
ID : 011132065

2. A spanning tree of a graph is just a sub graph that contains all the vertices and is a
tree.
A graph may have many spanning trees.
or or or
Some Spanning Trees from Graph AGraph A

3. All 16 of its Spanning TreesComplete Graph

4. The Minimum Spanning Tree for a given graph is the Spanning Tree of minimum
weight for that graph.
5
7
2
1
3
4
2
1
3
Complete Graph Minimum Spanning Tree

5. Kruskal's Algorithm
Prim's Algorithm
Boruvka's Algorithm

7. • The forest is constructed - with each node in a separate tree.
• The edges are placed in a priority queue.
• Until we've added n-1 edges
Extract the cheapest edge from the queue;
If it forms a cycle, reject it;
Else add it to the forest. Adding it to the forest will join two trees
together.
Every step will have joined two trees in the forest together, so that at the end,
there will only be one tree.

8. 4
1
2 3
2
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Complete Graph

9. 1
4
2
5
2
5
4
3
4
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
A AB D
B B
B
C D
J C
C
E
F
D
D H
J E G
F FG I
G GI J
H J JI

10. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Sort Edges
(in reality they are placed in a priority
queue - not sorted - but sorting them
makes the algorithm easier to visualize)

11. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Add Edge

12. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Add Edge

13. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Add Edge

14. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Add Edge

15. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Add Edge

16. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Cycle
Don’t Add Edge

17. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Add Edge

18. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Add Edge

19. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Add Edge

20. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Cycle
Don’t Add Edge

21. 2
5
2
5
4
3
4
4
10
1
6
3
3
2
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
B
B
D
J
C
C
E
F
D
D H
J
E G
F
F
G
I
G
G
I
J
H J
JI
1A D
4B C
4A B
Add Edge

22. 4
1
2
2 1
3
32
4
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Minimum Spanning Tree Complete Graph

23. Pseudo code
KRUSKAL(V, E, w)
{
A = ∅
For each v ∈ G.V
MAKE-SET(v)
sort E into non-decreasing order by w
For each (u, v) ∈ G.E taken from the sorted list
If FIND-SET(u) ≠ FIND-SET(v):
A = A ∪ {(u, v)}
UNION(u, v)
return A
}

24. Pseudo code Time Complexity
KRUSKAL(V, E, w)
{
A = ∅----------------------------------------------------------------O(1)
For each v ∈ G.V--------------------------------------------------O(V)
MAKE-SET(v)
sort E into non-decreasing order by w----------------------O(E lg E)
For each (u, v) ∈ G.E taken from the sorted list-----------O(E)
If FIND-SET(u) ≠ FIND-SET(v):
A = A ∪ {(u, v)}
UNION(u, v)
return A
}
T = O(1) + 0(V) +
O(E lg E) + O(E)
As
O(V) < O(E) <
O(E lg E)
T = O(E lg E)

26. • The new graph is constructed - with one node from the old graph.
• While new graph has fewer than n nodes
Find the node from the old graph with the smallest connecting edge to the
new graph;
Add it to the new graph.
Every step will have joined one node, so that at the end we will have one graph
with all the nodes and it will be a minimum spanning tree of the original graph.

27. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Complete Graph

28. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J

29. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J

30. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J

31. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J

32. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J

33. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J

34. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J

35. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J

36. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J

37. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J

38. 4
1
2
2 1
3
32
4
A
B C
D
E F
G
H
I
J
Complete Graph Minimum Spanning Tree
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J

39. Pseudo code
PRIM(V, E, w, r )
Q = { }
for each u in V
key[u] = ∞
π[u] = NIL
INSERT(Q, u)
DECREASE-KEY(Q, r, 0)
while Q is not empty
u = EXTRACT-MIN(Q)
for each v in Adj[u]
if v in Q and w(u, v) < key[v]
π[v] = u
DECREASE-KEY(Q, v, w(u, v))

40. Pseudo code Time Complexity
PRIM(V, E, w, r )
Q = { }
for each u in V-----------------------------------------O(V lg V)
key[u] = ∞
π[u] = NIL
INSERT(Q, u)
DECREASE-KEY(Q, r, 0)------------------------------O(lg V)
while Q is not empty--------------------------------O(E lg V)
u = EXTRACT-MIN(Q)
for each v in Adj[u]----------------------------O(E)
if v in Q and w(u, v) < key[v]
π[v] = u
DECREASE-KEY(Q, v, w(u, v))-------O(lg V)
T = 0(V lg V)+
O(lg V)+O(E lg V)
As
O(lg V) < O(V lg
V) < O(E lg V)
T = O(E lg V)

42. • Make a list of n trees, each containing a single node.
• While list has more than one tree
For each tree in the list, find the node not connected to the
tree with the smallest connecting edge to that tree
Add all the edges found to the new graph, thus creating a
new set of trees
Every step will have joined groups of trees, until only one tree remains.

43. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Complete Graph

44. • A
• B
• C
• D
• E
• F
• G
• H
• I
• J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Trees of the Graph at Beginning
of Round 1
List of Trees

45. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
1
4
A
B
D
Tree A

46. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
1
4
A
B
D
Edge A-D

47. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
4
4
10
A
B C
D
J
Round 1 Tree B

48. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
4
4
4
10
A
B C
D
J
Round 1 Edge B-A

49. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
4
2 1
B C
E F
Tree C

50. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
4
2 1
B C
E F
Edge C-F

51. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
1
5 6
4A
B
D
H
J
Tree D

52. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
1
5 6
4A
B
D
H
J
Edge D-A

53. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
2
2
C
E
G
Tree E

54. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
2
2
C
E
G
Edge E-C

55. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
3
1
5
C
F
G
I
Tree F

56. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
3
1
5
C
F
G
I
Edge F-C

57. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
2 3
3
4
E F
G
I
J
Tree G

58. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
2 3
3
4
E F
G
I
J
Edge G-E

59. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
2
5
D
H
J
Tree H

60. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
2
5
D
H
J
Edge H-J

61. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
3
5
3
F
G
I
J
Tree I

62. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
3
5
3
F
G
I
J
Edge I-G

63. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
3
4
2
6
10
B
D
G
H
I
J
Tree J

64. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1
3
4
2
6
10
B
D
G
H
I
J
Edge J-H

65. • A-D
• B-A
• C-F
• D-A
• E-C
• F-C
• G-E
• H-J
• I-G
• J-H
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 1 Ends -
Add Edges
List of Edges to
Add

66. • D-A-B
• F-C-E-G-I
• H-J
List of Trees
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Trees of the Graph at Beginning
of Round 2

67. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 2
4
1
2
2 1
3
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Tree D-A-B

68. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 2
4
1
2
2 1
3
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Edge B-C

69. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 2 Tree F-C-E-G-I
4
1
2 3
2 1
3
5
3
4
2
4
A
B C
D
E F
G
H
I
J

70. 4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 2 Edge I-J
4
1
2 3
2 1
3
5
3
4
2
4
A
B C
D
E F
G
H
I
J

71. 1
2
2 1
3
3
4
2
5 6
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 2 Tree H-J

72. 1
2
2 1
3
3
4
2
5 6
4
10
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Round 2 Edge J-I

73. • B-C
• I-J
• J-I
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
List of Edges to
Add
Round 2 Ends -
Add Edges

74. 4
1
2
2 1
3
32
4
A
B C
D
E F
G
H
I
J
4
1
2 3
2 1
3
5
3
4
2
5 6
4
4
10
A
B C
D
E F
G
H
I
J
Minimum Spanning Tree Complete Graph

75. Pseudo code Time Complexity
Input: A connected graph G whose edges have distinct weights
Initialize a forest T to be a set of one-vertex trees, one for each
vertex of the graph
While T has more than one component
For each component C of T
Begin with an empty set of edges S
For each vertex v in C
Find the cheapest edge from v to a vertex outside of C
and add it to S
Add the cheapest edge in S to T
Output: T is the minimum spanning tree of G.
If the edges are E
& vertices are V
then
T = O( E lg V )

76. Kruskal’s and Boruvka’s have better running times if the
number of edges is low, while Prim’s has a better running time
if both the number of edges and the number of nodes are low.
Boruvka’s avoids the complicated data structures needed for
the other two algorithms.
So, of course, the best algorithm depends on the graph and if
we want to bear the cost of complex data structures.