Embed presentation
Downloaded 12 times




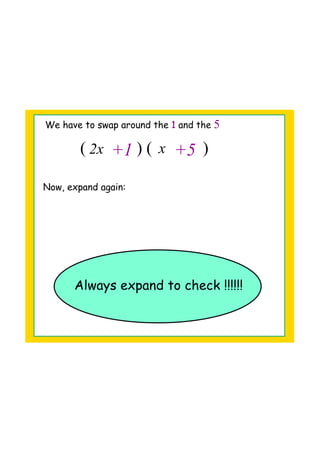



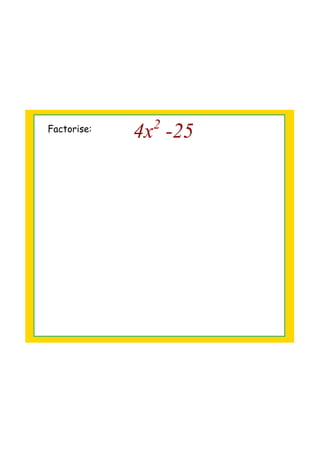


This document provides instructions on how to factorize quadratic expressions into their prime factors. It includes the following steps: - Factorize expressions of the form ax^2 + bx + c by finding two terms whose product is a and sum is b. - Always expand the factors to check the factorization is correct. - To factorize expressions with negative constants, list the factors of the constant term and try different pairings with the variables until expanding checks. - More complex expressions may require trial and improvement to find the correct factors.










